Попередня обробка результатів спостережень і техніко-економічної інформації

Економічні явища утворюються не як результат однозначного зв'язку причин і наслідку, а як результат складного переплетіння і взаємодії багатьох причин і наслідків.

Математико-статистичному моделюванню передує чітке уявлення суті вирішуваної задачі, аналіз її змісту з використанням технологічної, економічної і інженерної логіки. При цьому доцільно:

- вивчити літературу і узагальнити професійні знання про об'єкт дослідження;

- чітко сформулювати мету і завдання дослідження;

- визначити джерела, обсяг і методи отримання виробничо-економічної інформації;

- провести попередній якісний і кількісний математико-статистичний аналіз результатів спостережень.

При визначенні умов виробництва, що впливають на досліджуваний показник, слід дотримуватися апробованих принципів якісного аналізу:

- кожний чинник повинен бути теоретично обґрунтованим і змістовним, мати самостійне значення і не дублювати інші;

- вибіркові дані повинні бути представницькими, мати точне кількісне вимірювання, бути однорідними і зіставлюваними в часі й просторі.

Джерелами отримання виробничо-економічної інформації служать: статистична, бухгалтерська, виробничо-господарська, результати хронометражних спостережень і фотографії робочого часу, дані спеціальних обстежень і експериментів, що проводяться, експертні оцінки фахівців та інші матеріали.

Об'єктивність математико-статистичного моделювання багато в чому залежить від показовості (репрезентативності) й однорідності вибіркових даних.

Заздалегідь обґрунтовується обсяг вибірки n або перевіряється достатність початкової інформації для отримання математико-статистичних моделей заданої точності й надійності.

За теоремою Ляпунова для різних незалежних вибірок достатньо великого обсягу n, отриманих з однієї і тієї ж генеральної сукупності, середнє арифметичне підкоряється нормальному закону розподілу з дисперсією σу², рівної 1/n-ї частини дисперсії випадкової величини. При цьому максимальне відхилення є вибірковою середньою від генеральної середньої Ў, має назву стандартної помилки і визначається за формулою

Ў- =ţ_{α ,} (2.23)

де ţ_{α –} значення змінної в стандартизованому масштабі_.

ţ_α= (2.24)

визначається за інтегральною функцією Лапласа. Звідси

, (2.25)

де n – кількість спостережень.

Приклад. Встановити, при якому обсязі спостережень n вибірка є генеральною сукупністю, якщо Р=0,95 або 95%, ε=0,85 і σу=4,56?

Вирішення. Р=2Φ(ţ_α)=0,95 або Ф(ţ_α)= за нормованою інтегральною функцією Лапласа знаходимо ţ_α=1,96_. Звідси

спостережень

Виявлення спостережень, різко відмінних від основної маси вибіркових даних, ґрунтується на тому, що коли розподілені приблизно за нормальним законом, то найбільше відхилення від середнього значення за абсолютною величиною перевищує приблизно 3σу², тобто всі спостереження повинні розміщуватися в інтервалі

.

Точніше, контроль приналежності до досліджуваної вибірки різко відмінних значень проводиться при рівні значущості α з урахуванням обсягу вибірки n. При цьому визначається - 0,5,

а потім за таблицею інтегральної функції Лапласа знаходиться значення t_α і допустимий інтервал записується у вигляді

.

Приклад. Є вибірка обсягом n=150 спостережень. Середнє значення по вибірці =12,86; середнє квадратичне відхилення σу²=6,24; рівень значущості α =0,05; максимальне значення ознаки y_max =32,64, що вивчається; мінімальне – y_min =3,42. Визначити можливість використання в подальших дослідженнях y_max і y_min.

Вирішення. При заданому рівні , ţ_α =3,366.

Допустимий інтервал дорівнює

Всі спостереження можуть бути використані при подальшій обробці.

У разі, якщо початкова інформація отримана по декількох об'єктах або групах, необхідно перевірити її однорідність. Така перевірка ґрунтується на гіпотезі рівності вибіркових середніх обсягами n_i і n_j, отриманих з однієї генеральної сукупності.

З теореми Чебишева, що зі збільшенням обсягу вибірки її середнє значення прагне за вірогідністю до генеральної середньої, випливає наступний висновок: якщо по декількох вибірках достатньо великого обсягу з однієї і тієї ж генеральної сукупності буде знайдено вибіркові середні і , то вони будуть приблизно рівні між собою.

За умови незалежності вибірок і їх приналежності до єдиної нормально розподіленої генеральної сукупності для будь-яких двох вибірок i-ої і j-ої маємо ймовірність

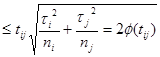{| |} , (2.26)

де σ_i², σ_j² – вибіркові дисперсії;

n_i, n_j – обсяги вибірок.

Наявні різниці відносяться до відповідної стандартної помилки. Як критерій перевірки приймають нормовану різницю, яку обчислюють на основі співвідношення: ,

що порівнюється з табличним значенням ţ_α, де 2Φ(ţ_α)=1-α.

Гіпотеза однорідності вибіркових даних затверджується при Р=2Φ(ţ_α)=0,95 і менше, тобто α=0,05 і більше. Це означає, що при всіх значеннях t_ij вся сукупність вихідних даних вважається приблизно однорідною і обробка може вестися по всьому масиву.

Приклад. По двох об'єктах зібрана інформація з наступними кількісними характеристиками: n₁=54; n₂=56; ₁=16,13; ₂=13,5; σ_y1²=65,3; σ_y2²=57,9.

Вирішення. Визначаємо t_ij(max) для y₁ і y₂:

Звідси Р=2Φ(1,76)=0,92 або 92%.

Гіпотеза про однорідність сукупності вибіркових даних затверджується з рівнем значущості α =0,08 або 8%.

Необхідність знання закону розподілу в кореляційному аналізі зумовлена насамперед обґрунтовуванням форми зв'язку між змінними.

Нормальний закон реалізується для випадкових величин, які формуються під сумарною дією багатьох відносно незалежних між собою причин, дія кожної з яких незначна в порівнянні із загальним результатом.

Результати спостережень обробляють в такій послідовності:

1. Вихідні дані розбиваються на інтервали і складають ряд розподілу функціональної ознаки y_i, визначають абсолютні й відносні частоти і будують гістограма розподілу;

2. Розраховують параметри закону розподілу і σ_y. Для спрощення рахункової роботи вводиться безрозмірна величина

y’_ср= , (2.27)

де - деяке інтервальне значення функції;

С_y – інтервальне значення Y _{icp ,} прийняте за центр угрупування;

∆y – інтервал зміни випадкової величини.

Дійсне значення и σ_y обчислюють на основі співвідношень , и .

3. Знаходять середнє інтервальне значення Y_icp в стандартизованому масштабі, відповідне центрам інтервалів. За допомогою диференціальної функції Лапласа для кожного ti знаходять значення f(t);

Визначають ординати теоретичної кривої розподілу і за знайденими точками будують теоретичну криву:

. (2.28)

Оцінюють ступінь згоди теоретичної кривої з дослідженими даними. Оцінку ступеня згоди частіш за все проводять за допомогою критерію χ² – «хі-квадрат» Пірсона, який є спеціально підібраною випадковою величиною, що визначається за формулою

, (2.29)

де k – число інтервалів угрупування змінної;

- емпіричні й теоретичні частоти.

Задаючись довірчим рівнянням значущості α=5%, за допомогою таблиці χ’² – розподілу за числом ступенів свободи

f=K-(S+1), (2.30)

де K –число інтервалів;

S – ступінь свободи

(для нормального розподілу S=2(,σ_y), оскільки необхідно скласти 2 рівняння для знаходження теоретичного розподілу і σ_y)

Встановлюють критичне значення χ’², з якими порівнюють розрахункове значення.

Якщо обчислене значення χ’² за дослідженими даними менше табличного, тобто воно потрапляє в область прийняття гіпотези Н₀, то теоретична крива розподілу узгоджується з емпіричним розподілом. Якщо чисельне значення χ’² перевершує табличне або рівне йому, тобто воно потрапляє в критичну область, дана гіпотеза Н₀ про форму кривої розподіл відкидається.

Приклад. Визначити закон розподілу витрат часу проходження рухомим складом маршруту між двома зупинками (хвил) при n=180 спостережень і y_min=0,70, y_max1,57 хв. .

Рис.2.4 - Гістограма розподілу

Рис. 2.5 - Гістограма і полігон розподілу

На підставі даних, представлених в табл. 2.1, отримуємо:

;

1)

;

2)

χ²_рас<χ²_табл. 5%.

Таким чином, теоретична крива розподілу зіставляється з емпіричним розподілом, що свідчить про наявність нормального розподілу.

Інтервал ∆y

Середнє значення інтервалу

Частота

Відносна частота

Умовні варіанти

Розрахунок середнього значення

Розрахунок дисперсії

Значення в стандартизованному масштабі

Значення диференціальної функції

Емпіричні розрахунки

Ординати теоретичного розподілу

Розрахункові частоти

yk-1-yk

ycp

mi

mi/n

Y’cp

miy’cp

f(t)

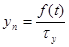
mi=yn∙n∆y

0,7 – 0,8 0,8 – 0,9 0,9 – 1,0 1,0 – 1,1 1,1 – 1,2 1,2 – 1,3 1,3 – 1,4 1,4 – 1,5 1,5 – 1,6

0,75   0,85   0,95   1,05   1,15   1,25   1,35   1,45   1,55

0,017   0,072   0,167   0,222   0,228   0,172   0,089   0,028   0,005

-4   -3   -2   -1

-12 -39   -60   -40

39,3132   89,2372   78,7320   15,3760     59,0364   90,6304   57,1220   19,1844

2,26   1,63   1,00   0,38   0,25   0,88   1,50   2,13   2,75

0,031   0,1057   0,2420   0,3712   0,3867   0,2709   0,1295   0,0413   0,0091

0,17   0,72   1,67   2,22   2,28   1,72   0,89   0,28   0,05

0,195   0,665   1,522   2,385   2,432   1,704   0,817   0,259   0,057

3,36   11,90   27,40   42,03   43,7   30,7   14,7   4,66   1,03

Таблиця 2.4 – Розрахунок показників нормального закону розподілу

Поиск по сайту: