АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задание 51 – 60

Читайте также:
  1. Window(x1, y1, x2, y2); Задание окна на экране.
  2. В основной части решается практическое задание.
  3. Домашнее задание
  4. Домашнее задание
  5. Домашнее задание
  6. Домашнее задание
  7. Домашнее задание
  8. Домашнее задание
  9. Домашнее задание
  10. Домашнее задание
  11. Домашнее задание
  12. Домашнее задание

 

Дана система линейных уравнений

 

 

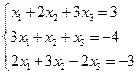
Решить систему а) матричным методом, б) методом Крамера, в) методом Гаусса.

а) данной системе соответствует матричное уравнение , которое решается по формуле: . Матрицы имеют вид:

 

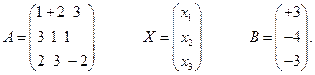
Находим обратную матрицу

 

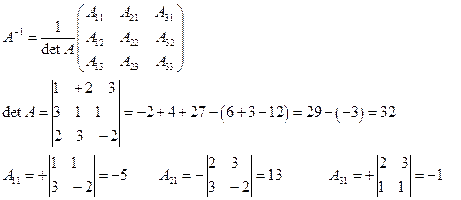
Находим матрицу

б) 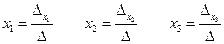- формулы Крамера. Вычислим все определители

 

в) Метод Гаусса.

Составим расширенную матрицу и преобразуем её с помощью элементарных преобразований.

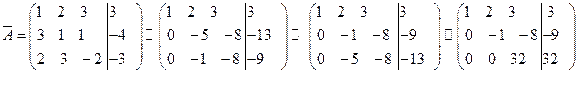
Из полученной матрицы, выделяя последнюю строку, видим, что исключены неизвестные и 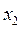. Найдём . .

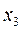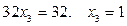Вторая строка соответствует уравнению:

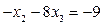или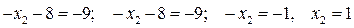

Аналогично из первой строки напишем уравнение:

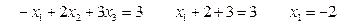
Итак: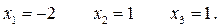

 

Задание 91 – 100.

Дано комплексное число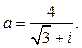

Записать число 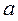в геометрической и тригонометрической формах и найти все корни уравнения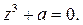

Рекомендуемая литература: Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. II, гл.III, §7, стр.97 – 101.

Найдём алгебраическую форму комплексного числа

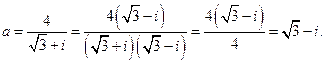
Тригонометрическая форма комплексного числа 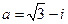определится по формуле .

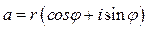Изобразив число на плоскости, найдём и .

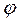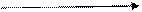
-1

 

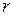
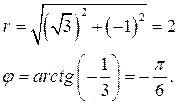
Итак, число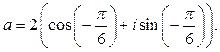

Найдём корни уравнения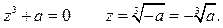

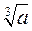вычислим по формуле Муавра

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

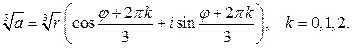
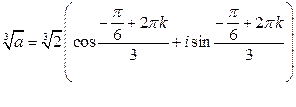
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)