Кинематика материальной точки твердого тела

Механикой называется раздел физики, посвященный изучению закономерностей простейшей формы движения материи – механического движения. Механическое движение состоит в изменении с течением времени взаимного расположения тел или их частей в пространстве.

Механика состоит из трех основных разделов: статики, кинематики и динамики. В статике рассматривают законы сложения сил и условия равновесия тел. В кинематике исследуют характеристики и закономерности различных типов механического движения тел безотносительно к тем причинам, которые обеспечивают осуществление рассматриваемого типа движения. В динамике изучают влияние взаимодействия между телами на их механическое движение.

Для описания движения тела в пространстве и времени используют физические модели. Простейшая физическая модель тела – материальная точка. Материальной точкой называется тело, формой и размерами которого в данной задаче можно пренебречь.

Если деформация тела при его взаимодействии с другими телами в рассматриваемом процессе пренебрежимо мала, то удобно пользоваться моделью абсолютно твердого тела. Абсолютно твердое тело – тело, расстояние между двумя точками которого в условиях данной задачи можно считать постоянным. Иначе говоря - это тело, формы и размеры которого не изменяются при его движении.

Положение тел в пространстве можно определить только по отношению к другим телам. Абсолютно твердое тело, по отношению к которому рассматривают движение исследуемого тела, называется телом отсчета. Совокупность тела отсчета и связанных с ним системы координат и часов называют системой отсчета.

Радиус-вектор ( ) – вектор, проведенный из начала координат в точку пространства, где расположена материальная точка (тело) (рис. 2.1.).

Кривая линия, по которой движется точка, называется траекторией движения. Длина дуги траектории за данный промежуток времени – путь (S), пройденный материальной точкой (рис. 2.1).

Перемещение ( ) – вектор, проведенный из начального положения точки в ее конечное положение (рис. 2.1.).

Рис.2.1.

Схематическое изображение движения материальной точки в пространстве

При движении точки ее радиус-вектор () и координаты () изменяются и являются функциями времени:

(2.1)

Уравнения (2.1) являются кинематическими уравнениями движения точки (уравнения координат движения точки).

В случае движения точки на плоскости уравнение траектории может быть представлено в следующем виде:

Для характеристики движения материальной точки также вводят векторную физическую величину – скорость, определяющую как быстроту движения, так и направление движения в данный момент времени t.

Вектором средней скорости точки в интервале от t до t+Dt называется

(2.2)

Из формулы (2.2) видно, что вектор средней скорости сонаправлен с вектором перемещения Если Dt ® 0, то

- мгновенная скорость.

(1.3)

Вектор мгновенной скорости направлен по касательной к траектории движения тела. В системе СИ единицей измерения скорости является

Скорость – величина относительная. В зависимости от выбора системы отсчета скорость точки различна. В этой связи вводят понятие скорости относительно неподвижной системы отсчета – абсолютная скорость и относительно подвижной системы отсчета – относительная скорость. При переходе из одной системы отсчета в другую можно использовать закон сложения скоростей: , где ­­­­­– абсолютная скорость (например, скорость пловца относительно берега), – относительная скорость (например, скорость пловца относительно реки); – скорость подвижной системы координат относительно неподвижной (например, скорость течения реки).

При неравномерном движении, кроме скорости, необходимо ввести другую характеристику – ускорение – меру быстроты изменения скорости.

Средним ускорением неравномерного движения в интервале Dt называется . Вектор среднего ускорения сонаправлен с вектором изменения скорости 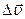. Ускорением или мгновенным ускорением точки в момент времени t называется величина

.

(2.4)

Основные виды прямолинейного движения:

1) Равномерное прямолинейное движе ние (рис. 2.2).

(2.5)

(2.6)

где - проекция скорости на ось OX. При прямолинейном движении .

(2.7)

где x₀ – координата материальной точки в начальный момент времени, S = x - x₀ – путь, пройденный материальной точкой за время t.

2) Равнопеременное прямолинейное движение (рис. 2.3)

(1.8)

(1.9)

где - проекция ускорения на ось OX, – начальная скорость точки в проекции на ось OX. При прямолинейном движении , .

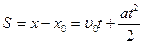
(2.10)

0 t   Рис. 2.3. Графическое изображение изменения скорости со временем при равноускоренном движении

Основные виды криволинейного движения:

1) Равномерное движение по окружности (рис. 2.4).

Линейная скорость–

(2.11)

где – длина дуги, по которой движется точка (тело). Зная радиус окружности можно определить (где N – число оборотов, которое сделала точка (тело) за время t; время одного оборота – период вращения ). В этом случае линейная скорость точки за­писывается в следующем виде:

(2.12)

Введя понятие частоты вращения ( ν) - как число оборотов в единицу времени получаем, что

(2.13)

При движении по окружности происходит изменение угла поворо­та j со временем относительно начала отсчета (см. рис. 2.4). Пос­леднее позволяет ввести понятие угловой скорости w, как изменение угла поворота за время :

(2.14)

Если в начальный момент времени 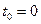начальный угол поворота , то Как известно (измеряется в радианах), а следовательно

(2.15)

Центростремительное (нормальное) ускорение :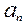

		(2.16)
2) Движение тела, брошенного под углом к горизонту	( )	(Рис.2.5.)

,

(2.17)

где – угол наклона к горизонту (см. рис. 2.5).

(2.18)

где 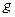– ускорение свободного падения,

(см. рис. 2.5),	(2.19)
	(2.20)

Дальность полета l определяется выражением:

(2.21)

Максимальная высота подъема :

(2.22)

Скорость движения тела, брошенного под углом к горизонту, записывается следующим образом:

(2.23)

2) Движение тела, брошенного горизонтально (рис. 2.6).

(2.24)

где h – высота в начальный момент времени, = 0 (см. рис.2.6),

(2.25)

(2.18)

где 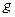– ускорение свободного падения,

(см. рис. 2.5),	(2.19)
	(2.20)

Дальность полета l определяется выражением:

(2.21)

Максимальная высота подъема :

(2.22)

Скорость движения тела, брошенного под углом к горизонту, записывается следующим образом:

(2.23)

3) Движение тела, брошенного горизонтально (рис. 2.6).

(2.24)

где h – высота в начальный момент времени, = 0 (см. рис. 2.6),

(1.25)

Положение произвольной материальной точки М в неподвижной и подвижной системах отсчета определяется радиусами вектора и , причем

(2.28)

В проекциях на оси координат это векторное равенство записывается в следующем виде, называемом преобразованием координат Галилея:

(2.29)

В классической механике принимается, что ход времени не зависит от относительного движения систем отсчета. Поэтому систему (1.29) можно дополнить еще одним уравнением:

Принцип относительности Галилея часто формулируется следующим образом: равномерное и прямолинейное движение системы как целого не влияет на ход протекающих в ней механических процессов.

Движение точки М относительно неподвижной системы отсчета будем называть абсолютным движением. Движение точки М относительно подвижной системы отсчета будем называть относительным движением. Скорость точки М относительно неподвижной инерциальной системы координат называется абсолютной скоростью точки М. Скорость точки М относительно подвижной инерциальной системы координат называется относительной скоростью точки М. Скорость подвижной системы (то есть жестко связанной с этой системой), через которую в данный момент проходит рассматриваемая нами материальная точка М называется переносной скоростью точки М.

Дифференцируя уравнение (2.28) по времени, и учитывая, что , найдем соотношение между скоростями точки М относительно обеих систем:

.

(2.31)

Таким образом, абсолютная скорость точки М равна сумме ее переносной и относительной скоростей. Уравнение (2.31) называется законом сложения скоростей в классической механике.

Табл. 2.1. Таблица аналогий

КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ	КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ	ФОРМУЛЫ СВЯЗИ

Поиск по сайту: