Уравнение времени

В астрономии так называемое «среднее солнце» - как некоторая фиктивная точка принимается за указатель среднего солнечного времени, т.е. среднее солнечное время отсчитывается часовым углом «среднего солнца». Момент его верхней кульминации – местный средний полдень (с 1 января 1925 г. этому моменту приписали 12^ч, по международному соглашению). То есть местное время стали определять по формуле Т_m = 12^ч + t_m, [6, с. 55].

Часовой угол t_m «среднего солнца» определяется вычислениями: звездное время по «среднему солнцу» равно s = t_m + a_m, а по истинному Солнцу – s = t_¤ + a_¤; приравнивая их друг другу, выразим часовой угол t_m:

t_m = t_¤ + a_¤ – a_m = t_¤ – h.

h = a_¤ – a_m называется уравнением времени, эта величина может быть заранее вычислена на основании известных закономерностей движения Земли.

Уравнением времени h устанавливается связь между двумя системами счета солнечного времени, представляющей собой разность (поправку) между средним временем и истинным солнечным временем:

h = Т_m - Т_¤.

Уравнение времени можно рассматривать как разность между часовыми углами «среднего солнца» и истинного Солнца:

h = t_m - t_¤.

Значения уравнения времени приводятся для каждого дня года в астрономических календарях-ежегодниках.

На практике астрономы не определяют часовой угол Солнца, а наблюдают Солнце в момент истинного полудня, когда t_¤ = 0. В этом случае t_m = h (часовой угол «среднего солнца» равен уравнению времени).

Примерный график уравнения времени имеет вид (рис. 1.4.4) [6, с. 55], а приближенные значения уравнения времени приведены в таблице 1 [6, с. 56], которую можно интерполировать, а также нанести на график, построенный в удобном масштабе.

Таблица 1

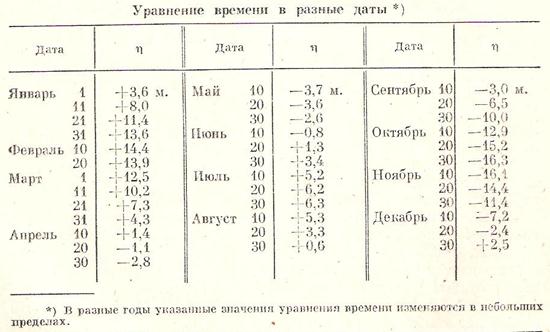
Характер изменения значений уравнения времени h в течение года в [2, с. 145-146] представлен графиком (рис. 1.4.5), построенный по следующим данным:

1 января h = +3^м,4, 27 июля h = +6^м,4,

11 февраля +14,4, 1 сентября 0,0,

16 апреля 0,0, 3 ноября –16,4,

15 мая –3,8, 25 декабря 0,0,

14 июня 0,0.

По графику значение h можно определять на заданную дату с точностью ±0^м,5.

Таким образом, определение местного солнечного времени Т_m сводится к установлению часового угла t_¤ Солнца из наблюдений и выборке h и справочника и вычислению по формуле: Т_m = t_¤ + h + 12^ч.

Практически среднее время определяют по непосредственному измерению часового угла Солнца и уравнению времени из астрономического календаря:

Т_m = Т_¤ + h = t_¤ + 12^ч + h.

В истинный полдень t_¤ = 0^ч среднее время равно Т_m = 12^ч + h.

Когда Солнце обгоняет среднее солнце, т.е. a_¤ > a_m, уравнение времени h > 0 и Т_l > Т_¤, средний полдень наступает раньше истинного полдня. Когда a_¤ < a_m – все наоборот, и средний полдень наступает позже истинного полдня.

Наибольшие расхождения наступают 12 февраля (h = +14^м17^с) и 3 – 4 ноября (h = -16^м24^с). И четыре раза в год 15 – 16 апреля, 13 – 14 июня, 1 сентября и 25 декабря, уравнение времени h = 0.

Среднее время на Гринвичском меридиане называется средним гринвичским временем или всемирным временем Т₀ (Международное обозначение UT).

Очевидно:

Т_m = Т₀ + l.

Для двух географических пунктов Т_m2 - Т_m1 = l₂ - l₁.

Средним временем в своей местности практически пользовались почти до конца 19 века.

Поиск по сайту: