АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

При ускорении частицы (а) и его структура (б)

Читайте также:
  1. B) социально-стратификационная структура
  2. III. СТРУКТУРА И ОРГАНЫ УПРАВЛЕНИЯ ПРИХОДА
  3. VI. Рыночный механизм. Структура рынка. Типы конкурентных рынков
  4. VIII. Формирование и структура характера
  5. А. Лінійна організаційна структура
  6. Автоматизовані банки даних (АБД), їх особливості та структура.
  7. Адміністративна структура БМР має три органи: загальні збори акціонерів, рада директорів і правління.
  8. Адхократическая структура
  9. Акти застосування права: поняття, ознаки, види, структура
  10. АЛЕКСИТИМИЯ И ПСИХОСОМАТИЧЕСКАЯ СТРУКТУРА
  11. Анормальная структура мозга
  12. Античастицы. Аннигиляция.

В промежутке между моментами t1 и t2 (в пространстве – точками х1 и х2) функция 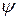представляет собой волновой пакет, аналитически выражаемый формулой

(11.7,а)

где

(11.7,б)

(11.7,в)

Выведем эту формулу из уравнения Шредингера для свободной частицы (11.4). Её скорость в момент t(t1<t<t2) равна этому значению, скорости соответствуют кинетическая энергия и импульс:

.

Подставляя их в уравнение Шредингера (11.3,а) и решая его, находим соответствующую волновую функцию в виде синусоидальной волны (11.5). Поскольку в этом интервале времени скорость vt непрерывно меняется, вместе с ней меняется и волновая функция . При появлении новой функции через интервал времени dt предшествующая функция остается. Происходит последовательное сложение волн, возникших сначала, с волнами, появившимисяпозднее. Поэтому результирующая волна равна сумме (фактически интегралу) . Для того, чтобы произвести такое суммирование, запишем функцию в следующем виде

(11.8,а)

где ω и k определяются соотношениями (11.7,а), δк и групповая скорость (скорость группы волн) v2 равны:

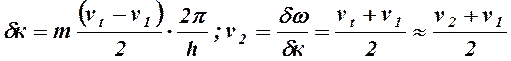(11.8,б)

В формулах (11.8,б) предусматривается, что

Иными словами, скорость частицы изменяется в течение рассматриваемого интервала времени незначительно и групповую скорость v2 можно принять постоянной. Переменной величиной оказывается только приращение волнового числа δк. По нему и осуществляется суммирование волновых функций:

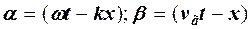(11.9,а)

После интегрирования (11.8,а) и ряда несложных тригонометрических преобразований получаем:

С учетом (11.7,б), (11.7,в) и (11.8,б) получаем (11.7,а).

Величину в формуле (11.7,а) находим, исходя из того, что интеграл квадрата волновой функции (11.7,а) в пределах от до равен единице, если ≥h/π, т. е. соблюдается принцип неопределенности Гейзенберга.

Иными словами

и, следовательно

Подставляя в (11.7,а), получаем окончательно

(11,9,б)

На рис. 11.2,б показан волновой пакет, соответствующий этой функции. Итак, мы видим, что применение аппарата волновой функции, определенной уравнением Шредингера, действительно аналитически позволяет установить частицу в какой – либо области пространства, если она начнет двигаться ускорено, причем это движение будет длиться столько, сколько определяется уравнением неопределенности Гейзенберга.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)