|
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Упражнения для самостоятельного выполнения
1. Выполнить поразрядное логическое сложение и умножение двоичных чисел:
а) 101 и 110; б) 10101 и 11100; в) 110011 и 111100.
2. Преобразовать следующие логические выражения:

3. Доказать, что число логических функций двух логических переменных равно 16.
4. Реализовать модифицированные таблицы истинности логических схем НЕ, ИЛИ, И-НЕ, ИЛИ-НЕ (см. рис. 4.5), используя программу MS Excel.
5. Составить таблицы истинности для следующих логических функций:

6. Записать выражения для логических функций F1 и F2 в виде СДНФ и СКНФ. Логические функции F1 и F2 представлены далее соответственно таблицами истинности.

7. По заданному преподавателем варианту таблицы N составить таблицу истинности логической функции F, используя таблицу М. Найти выражение для логической функции F, осуществить ее преобразование в соответствии с основными законами алгебры логики и разработать логическую схему полученной функции с использованием логических схем НЕ, И, ИЛИ. Для графического отображения разработанной логической схемы использовать любой графический редактор.
Таблица М 
Таблица N 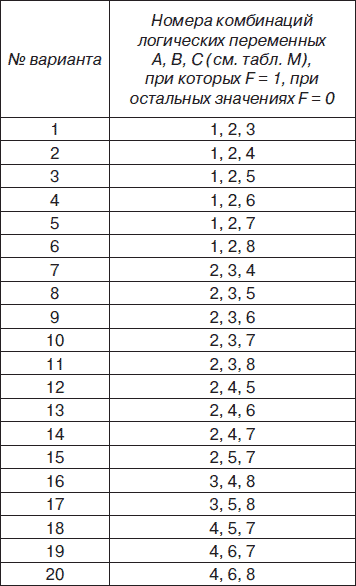
29) Классификация цифровых устройств
По принципу действия все логические устройства делятся на два класса: комбинационные схемы и цифровые автоматы (последовательностные устройства).
Комбинационными схемами (автоматами без памяти) называют логические устройства, выходные сигналы которых (выходное слово Y) в любой дискретный момент времени t i однозначно определяются только входными сигналами (входным словом Х), поступающими в тот же момент времени.
Комбинационную схему можно представить в виде т - k -полюсного элемента (рисунок 2). Входное двоичное слово (входной алфавит) комбинационной схемы задается набором символов хi (Х = (х1 х2... хт)), а выходное слово (выходной алфавит) принимает значения из выходных символов уj (Y = (у1 у2 ... уk).
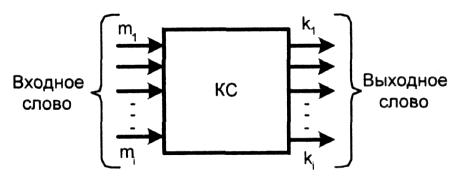
Рисунок 2
Закон функционирования КС определен, если задано соответствие между ее входными и выходными словами, например, словесно, в виде таблицы истинности или в аналитической форме с использованием булевых функций.
Цифровым автоматом (последовательностным устройством) называют логическое устройство, выходные сигналы которого (выходное слово Y) определяются не только действующей в данный момент времени ti комбинацией входных переменных (входным словом Х), но и внутренним состоянием устройства, которое явилось результатом воздействия на него входных слов в предыдущие такты (ti-1, ti-2 и т.д.).
Таким образом, комбинация входного слова и текущего состояния автомата в данном такте определяет не только выходное слово, но и то состояние, в которое автомат перейдет к началу следующего такта.
Цифровой автомат содержит память, состоящую из запоминающих элементов (ЗЭ) - триггеров, элементов задержки и др., фиксирующих состояние, в котором он находится. Комбинационная схема не содержит ЗЭ. Поэтому ее и называют автоматом без памяти или примитивным автоматом.
Структурная схема цифрового автомата показана на рисунке 3. Автомат с памятью задается тремя наборами переменных: Х, Y и Q, где Q – набор переменных, которые отображают внутреннее состояние схемы.
Рисунок 2
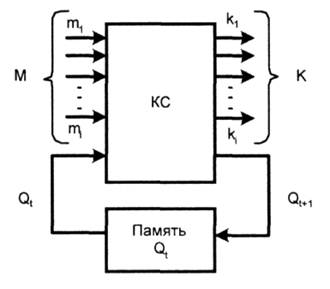
Для описания цифрового автомата должны быть указаны:
а) входной алфавит Х = (х1, х2, …, хт);
б) выходной алфавит Y = (у1, у2, …, уk);
в) алфавит внутренних состояний Q = (q1, q2, …, ql);
г) начальное состояние автомата Qt;
д) функцию перехода А (Q, х), однозначно определяющую зависимость состояния автомата Q (t + 1) в такте t + 1 от состояния автомата Q (t) и входного сигнала x (t) в такте t и функцию выходов В (Q, х), однозначно определяющую зависимость выходного сигнала Y (t) от состояния автомата Q (t) и входного сигнала x (t) в такте t.
Различают два типа цифровых автоматов.
Автомат, у которого выходные переменные в любом такте ti зависят от внутреннего состояния и от входных переменных, называется автоматом Мили и задается уравнением
уj = f (Qi, хi).
Автомат, у которого выходные переменные в любом такте ti зависят только от внутреннего состояния в ti- 1 - мтакте, называется автоматом Мура и задается уравнением
yi = f (Qi).
Примером автомата Мура является триггер.
Функции переходов и выходов могут задаваться различными способами, например, в форме таблиц или с помощью графов. При задании в виде графов состояния автомата представляются вершинами, а переходы из состояния в состояние - дугами. На дугах указываются значения входных сигналов, вызывающих соответствующие переходы. Выходные сигналы автомата Мура указываются рядом с вершинами графа. Выходные сигналы автомата Мили, вырабатываемые перед переходом, указываются на соответствующих дугах.
Для описания алгоритмов работы и структуры комбинационных схем используют аппарат алгебры логики (булевой алгебры). Этот аппарат применим к двоичным (булевым) переменным.
Булевыми переменными называются переменные х1, х2, …, хп, которые могут принимать только два значения – 0 и 1. Функция от двоичных переменных f (x1, х2,..., хп) называется булевой функцией (логической функцией), если она, так же как и ее аргументы, принимает только два значения: 0 и 1.
В основе алгебры логики лежит три логических операции:
- логическое отрицание (операция НЕ, инверсия), обозначаемое надчеркиванием над логической переменной или логическим выражением;
- логическое сложение (операция ИЛИ, дизъюнкция), обозначаемое знаком «+» или «Ú»;
- логическое умножение (операция И, конъюнкция), обозначаемое одним из знаков: «´», «×», «&» или «Ù».
Каждая логическая операция задает соответствующую логическую функцию. Следовательно, можно говорить о трех логических (булевых) функциях: конъюнкции (х 1 & х 2), дизъюнкции (х 1 + x 2), инверсии ( ). Число аргументов (переменных) функций дизъюнкции и конъюнкции в общем случае может быть произвольным (больше двух).
). Число аргументов (переменных) функций дизъюнкции и конъюнкции в общем случае может быть произвольным (больше двух).
Система булевых функций называется функционально полной, если при помощи функций, входящих в систему, можно выразить любую сколь угодно сложную булеву функцию.
В математической логике доказывается, что если система булевых функций содержит функции конъюнкции, дизъюнкции и инверсии, то она является функционально полной.
Функциональной полнотой обладают и некоторые другие системы, например, система, состоящая из одной булевой функции И – НЕ («штрих Шеффера»,  ) и система, содержащая единственную булеву функцию ИЛИ – НЕ («стрелка Пирса»,
) и система, содержащая единственную булеву функцию ИЛИ – НЕ («стрелка Пирса»,  ).
).
Для физической реализации булевой функции в технике используется комбинационная схема, выполняющая соответствующее этой функции преобразование информации (то есть, логические операции над двоичными переменными). Такую комбинационную схему называют логическим элементом.
Логическим элементом называется физическое устройство, реализующее одну из операций алгебры логики или простейшую логическую функцию. Схема, составленная из конечного числа логических элементов, называется логической схемой.
Число входов логического элемента соответствует числу аргументов воспроизводимых им одной или нескольких булевых функций.
Подобно тому, как сложная булева функция может быть получена суперпозицией более простых функций, так и сложная комбинационная схема строится из элементарных схем – из логических элементов.
| х 0 | у = 
|
Набор логических элементов для построения комбинационных схем является функционально полным, если реализуемые этими элементами булевы функции образуют функционально полную систему функций. Так функционально полным является набор, состоящий из трех логических элементов – инвертора, конъюнктора и дизъюнктора. Условные графические обозначения и таблицы истинности этих элементов показаны, соответственно, на рисунках 3, 4, 5.
 Рисунок 3
Рисунок 3
| х 1 | х 0 | у = х 0× х 1 |
 0 0
| ||
Рисунок 4
| х 1 | х 0 | у = х 0 + х 1 |
 0 0
| ||
Рисунок 5
Как отмечалось ранее, функциональной полнотой обладают логические функции отрицание конъюнкции (И-НЕ) и отрицание дизъюнкции (ИЛИ-НЕ), для реализации которых используются соответствующие элементы Шеффера (И-НЕ) и Пирса (ИЛИ-НЕ). Условные графические обозначения и таблицы истинности этих элементов приведены, соответственно, на рисунках 6 и 7.
 х 2 х 2
| х 1 | 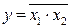
|
Рисунок 6
| х 2 | х 1 | 
|
 0 0
| ||
Рисунок 7
Системой логических элементов называется предназначенный для построения цифровых устройств функционально полный набор логических элементов, объединяемый общими электрическими, конструктивными и технологическими параметрами, использующий одинаковый способ представления информации и одинаковый тип межэлементных связей. Система элементов чаще всего избыточна по своему функциональному составу, что позволяет строить схемы, более экономные по числу использованных элементов. Системы элементов содержат элементы для выполнения логических операций, запоминающие элементы, элементы, реализующие функции узлов ЭВМ, а также элементы для усиления, восстановления и формирования сигналов стандартной формы.
Элементы, входящие в состав системы, представляют собой микроминиатюризованные интегральные электронные схемы (микросхемы), сформированные в кристалле кремния с помощью специальных технологических процессов.
В большинстве современных систем (серий) элементов имеются микросхемы малой степени интеграции (ИС), средней степени интеграции (СИС) и большой степени интеграции (БИС). Логические элементы в виде схем ИС реализуют совокупность логических операций, таких, как И, ИЛИ, И - ИЛИ, И - НЕ, ИЛИ - НЕ, И - ИЛИ - НЕ и триггеры. Логические элементы на микросхемах СИС и БИС реализуют узлы ЭВМ.
Основными параметрами системы логических элементов являются:
- уровни питающих напряжений;
- уровни сигналов для представления логических 0 и 1;
- нагрузочная способность (коэффициент разветвления по выходу);
- помехоустойчивость;
- рассеиваемая мощность;
- быстродействие.
По типам базовых элементов электронных ключей разделяют несколько типов интегральных элементов, где наиболее распространенными являются следующие:
а) транзисторно-транзисторная логика (ТТЛ);
б) эмиттерно-связанная логика (ЭСЛ);
в) инжекционная интегральная логика (И2Л);
г) структуры металл-оксид-полупроводник р- ипа (р -МОП);
д) структуры металл-оксид-полупроводник п -типа (п -МОП);
е) комплементарные МОП-структуры (КМОП);
ж) динамические МОП-структуры.
Логические схемы, которые изготовляются на разной конструктивно-технологической основе, значительно различаются по своим характеристикам, даже если они реализуют одинаковые функции. У любого из указанных видов схемотехники имеются свои преимущества и недостатки. Так, ЭСЛ отличается высоким быстродействием, хотя некоторые разновидности ТТЛ приближаются к ней по этому параметру. Как р -МОП-, так и п -МОП-логика широко применяются в микропроцессорах, а КМОП-схемотехника пользуется преимуществом, если важно уменьшить потребляемую мощность.
Динамические МОП-структуры используются для построения различных запоминающих устройств. Они имеют простую организацию, в которой логическое состояние определяется зарядом емкости, внутренне присущей логическому элементу. И2Л применяется в интегральных схемах.
Основные параметры ИМС ТТЛ, ЭСЛ и КМОП приведены, соответственно, в таблицах 1, 2 и 3.
Таблица 1 – Основные параметры ИМС ТТЛ
| Серия ИМС | Потребляемая мощность, мВт | Задержка распространения, нс | Максимальная частота, МГц | Коэффициент разветвления |
| 10,0 | ||||
| 33,0 | ||||
| 6,0 | ||||
| 9,5 | ||||
| 3,0 | ||||
| КР1533 | 4,0 | |||
| КР1531 | 2,0 |
Таблица 2 – Основные параметры ИМС ЭСЛ
| Серия ИМС | Потребляемая мощность, мВт | Задержка распространения, нс | Коэффициент разветвления | Напряжение питания, В |
| 100, 500 | 2,90 | -5,2 | ||
| 0,75 | -4,5 |
Таблица 3 – Основные параметры ИМС КМОП
| Серия ИМС | Потребляемая мощность, мВт | Задержка распро-странения, нс | Максимальная частота, МГц | Коэффициент разветвления | Напряж. питания, В |
| 164, | |||||
| 561, | 3... 15 | ||||
| КР1561 | 3... 18 | ||||
| 2... 6 |
Триггер – простейшее последовательностное логическое устройство, обладающее способностью длительное время находиться в одном из двух возможных состояний и переходить из одного состояния в другое лишь под воздействием внешних сигналов.
В отличие от комбинационных логических схем, триггеры – это логические устройства с памятью. Их выходные сигналы в общем случае зависят не только от сигналов, приложенных к входам в данный момент времени, но и от сигналов, воздействовавших на них ранее (то есть, от внутреннего состояния триггера). Триггеры являются базовыми элементами для построения других последовательностных логических устройств (делителей частоты, регистров, счетчиков и др.).
Входы триггера разделяют на информационные и управляющие (вспомогательные). Информационные входы используются для управления состоянием триггера. Управляющие входы обычно используются для предварительной установки триггера в некоторое состояние и для синхронизации.
Триггеры, как правило, имеют 2 выхода: прямой Q и инверсный  .
.
Входы триггеров принято обозначать следующим образом (таблица 4):
| Обозначение | Назначение |
| S | Вход установки триггера в состояние «1» |
| R | Вход установки триггера в состояние «0» |
| T | Счетный вход триггера |
| J | Вход установки в состояние «1» в универсальном триггере |
| K | Вход установки в состояние «0» в универсальном триггере |
| D | Информационный вход установки триггера в состояние «0» или «1» (задержка) |
| V | Управляющий вход для разрешения приема информации |
| C | Вход синхронизации – разрешает схеме управления запись информации в триггер |
Триггер в общем случае можно представить в виде схемы, приведенной на рисунке 8.
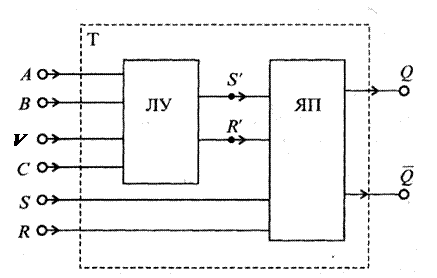
Рисунок 8
Как показано на схеме, в общем случае триггер состоит из ячейки памяти (ЯП) и логического устройства (ЛУ) управления, преобразующего входную информацию в комбинацию сигналов, под воздействием которых ЯП принимает одно из двух устойчивых состояний (0 или 1).
Информационные сигналы поступают на входы А и В (в каждом конкретном триггере это может быть один из входов Т, D или др.) ЛУ и преобразуются в сигналы, поступающие на внутренние входы S ’ и R ' ЯП. Процесс преобразования информационных сигналов осуществляется при воздействии сигналов, подаваемых на вход V разрешения приема информации и вход С синхронизации, обеспечивающий тактируемый прием информации.
В простейшем триггере ЛУ может отсутствовать, а информационные сигналы подаются непосредственно на входы S и R ЯП.
В зависимости от свойств, числа и назначения входов триггеры можно разделить на несколько видов. При этом классификация триггеров существует по нескольким признакам. Наиболее распространенной является классификация:
- по способу записи информации (асинхронные, синхронные);
- по способу синхронизации (статические, динамические);
- по способу организации логических связей.
По способу организации логических связей триггеры делятся на следующие классы:
- с раздельной установкой состояния «0» и «1» (RS -триггер);
- универсальный (JK -триггер);
- с приемом информации по одному входу D (D -триггер или элемент задержки на один такт);
- со счетным входом Т (Т -триггер).
В асинхронных триггерах изменение состояния происходит непосредственно в момент появления соответствующего информационного сигнала на входах А и В. Всинхронном триггере изменение состояния (в соответствии с информационными сигналами на входах А и В) может произойти только в момент присутствия соответствующего сигнала на входе С. При этом синхронизация может осуществляться импульсом (потенциалом) или фронтом импульса (перепадом потенциала из низкого уровня в высокий или из высокого в низкий). В первом случае сигналы на информационных входах оказывают влияние на состояние триггера только при разрешающем потенциале на входе С. Во втором случае воздействие информационных сигналов проявляется только в момент изменения потенциала на входе С. Универсальные триггеры могут работать как в синхронном, так и в асинхронном режимах.
Кратко рассмотрим некоторые основные типы триггеров.
Закон функционирования триггеров обычно описывают таблицей переходов, которую иногда также называют таблицей истинности.
Условное графическое обозначение и таблица переходов асинхронного RS -триггераприведены ниже.
| Номер набора | R | S | Qt | Qt+1 |
| * | ||||
| * |

Триггер имеет два информационных входа S (от англ. set)и R (от англ. reset) и два выхода – прямой Q и инверсный  .
.
Триггер может быть реализован на логических элементах И-НЕ или ИЛИ-НЕ. В частности, логическая схема RS -триггера, реализованного на базе ЛЭ ИЛИ-НЕ, приведена ниже (рисунок 9).

Рисунок 9
Функционирование RS -триггера состоит в следующем. При подаче на вход S логической 1 на инверсном выходе  формируется логический 0. Поскольку этот сигнал по цепи обратной связи подается на один из входов верхнего элемента ИЛИ-НЕ, а на другом его входе также действует сигнал логического 0 со входа R, на выходе Q устанавливается уровень, соответствующий логической 1. Это состояние триггера может сохраняться сколь угодно долго и не зависит от последующих изменений сигнала на входе S, если на входе R поддерживается состояние «0».
формируется логический 0. Поскольку этот сигнал по цепи обратной связи подается на один из входов верхнего элемента ИЛИ-НЕ, а на другом его входе также действует сигнал логического 0 со входа R, на выходе Q устанавливается уровень, соответствующий логической 1. Это состояние триггера может сохраняться сколь угодно долго и не зависит от последующих изменений сигнала на входе S, если на входе R поддерживается состояние «0».
Для RS -триггера комбинация S = 1 и R = 1 является запрещенной. После такой комбинации информационных сигналов состояние триггера будет неопределенным (в таблице переходов обозначено «*»): на его выходе Q может быть 0 или 1.
При R = 1 (S = 0) на выходе Q получим сигнал Q = 0, а соответствующий канал обратной связи обеспечит на инверсном выходе сигнал логической единицы и т. д.
Условное графическое обозначение асинхронного RS -триггера показано на рисунке 10. Такие триггеры входят во все типы более сложных триггеров.

Рисунок 10
Простейший синхронный RS -триггер содержит кроме ЯП еще и ЛУ. На рисунке 11 показана функциональная схема и условное графическое обозначение такого триггера, реализованного на логических элементах И-НЕ.

Рисунок 11
Переключение RS -триггера, изображенного на рисунке, производится только при наличии сигнала «1» на одном из информационных входов и сигнала «1» на входе синхронизации С.
Регистром называется последовательностное логическое устройство, предназначенное для хранения п- разрядного машинного слова и для выполнения над ним поразрядных логических операций. К таким операциям можно отнести:
- прием, хранение и выдача машинного слова;
- преобразование последовательного кода в параллельный и наоборот;
- сдвиг слова влево или вправо на заданное число разрядов.
В качестве элементов памяти в регистре используется совокупность триггеров, число которых равно разрядности регистра (числу разрядов двоичного слова, подлежащих хранению). Кроме этого регистр содержит комбинационную схему, позволяющую выполнять над двоичным словом перечисленные выше операции.
Различают два вида регистров:
- накопительные (регистры памяти);
- сдвигающие.
Сдвигающие регистры делятся:
а) по способу ввода-вывода информации на:
- параллельные;
- последовательные;
- комбинированные;
б) по направлению передачи информации на:
- однонаправленные;
- реверсивные.

Рассмотрим накопительный регистр с параллельным вводом и выводом информации. Основой регистра являются D-триггеры, которые на своих выходах повторяют значения сигналов на входах X, —Х4 (информационные входы) при логическом сигнале 1 на входе синхронизации (т. е. осуществляется параллельный ввод входной информации в регистр). На четырех двухвходо-вых элементах «И» реализованы схемы совпадения, входные сигналы которых совпадают с выходными сигналами триггеров в том случае, когда на вход Y2 подана логическая единица. Таким образом осуществляется параллельный вывод информации.
В качестве примера рассмотрим микросхему регистра К155ИР15. Приведем условное обозначение и таблицы внутренних и выходных состояний.
Микросхема К155ИР15 представляет собой четырехразрядный параллельный регистр памяти с тремя входными состояниями. Микросхема имеет следующие выводы: Dl—D4— информационные входы, Q\—Q^— выходы регистра, С — вход синхронизации, R — вход сброса триггеров регистра в нулевое состояние, входы Е1 и Е2 - для управления режимом работы регистра, Ezj и Ez2 — для перевода выходов регистра в высокоимпедансное состояние.

|
При El = Е2 = 0 осуществляется параллельный ввод информации со входов DI—
D4 при воздействии положительного перепада на входе синхронизации С.
Хранение информации осуществляется, если хотя бы на одном из входов Е1 или Е2 действует логическая 1.
При подаче 1 на вход R осуществляется сброс триггеров регистра.
Если хотя бы на одном из входов EZ, или EZ2 действует логическая 1, то все выходы отключены, т. е. они переведены в высокоимпедансное состояние.
На рис. 3.122 представлен сдвигающий регистр. В исходном состоянии на выходах всех триггеров логический сигнал «О». При подаче логического сигнала «1» младшего разряда числа на вход 1-го триггера он запоминается в нем в момент действия положительного перепада тактового импульса. Состояние же остальных триггеров не меняется, так как на их входах были логические сигналы «О». Во время второго тактового импульса на входе первого триггера действует логический сигнал «О», на входе второго триггера — логический сигнал «1», на входе третьего и четвертого — логические сигналы «О». Эти сигналы запоминаются триггерами, на входе которых они действовали, т. е. осуществляется сдвиг единицы вправо, и т. д. Таким образом, за четыре такта осуществляется последовательный ввод в регистр 4-разрядного двоичного числа.

В качестве примера приведем микросхему сдвигающего регистра К155ИР13 и его таблицу состояний.

Микросхема К155ИР13 является универсальным восьмиразрядным реверсивным сдвигающим регистром и может работать в режимах последовательного ввода информации со сдвигом вправо или влево, параллельного ввода информации, хранения информации, сброса (установки нулей).
Микросхема имеет следующие входы:
Dl—D8 — для параллельного ввода информации, DR и DL — информационные входы для последовательного ввода информации при сдвиге, соответственно вправо или влево, входы 51 и 60 — для выбора режима работы, R -вход сброса триггеров регистра в нулевое состояние и С — вход синхронизации.
Сброс триггеров осуществляется при подаче логического 0 на вход R.
При S\ = О и SQ = 1 осуществляется последовательный ввод информации со входа DR в первый разряд регистра со сдвигом вправо.
При SI = 1,.50 = 0 осуществляется последовательный ввод информации со входа DL в восьмой разряд регистра со сдвигом влево.
При 51 = 50 = 1 осуществляется параллельная запись информации со входов Dl—D8 при воздействии положительного перепада на входе синхронизации С.
При 51 = iSO = 0 осуществляется режим хранен! я информации.
Счетчиком называют последовательностное цифровое устройство (цифровой автомат), предназначенное для подсчета числа импульсов. Счетчики находят применение в ЭВМ для формирования адресов команд, подсчета числа выполненных операций и др.
В процессе работы счетчик последовательно изменяет свое состояние (сигналы на выходах) в определенном порядке. Количество разрешенных состояний счетчика называется коэффициентом счета Ксч. Одно из возможных состояний счетчика принимается за начальное. Если счетчик начал счет от начального состояния, то каждый импульс, кратный модулю счета Кс, снова устанавливает счетчик в начальное состояние.
Для синтеза счетчиков используются D-, T- или JK-триггеры, соединенные определенным образом. Существует несколько способов классификации счетчиков. В частности, по направлению счета счетчики делятся на: суммирующие, вычитающие и реверсивные.
Если выходные коды счетчика при поступлении входных импульсов изменяются в возрастающем порядке, то счетчик называют суммирующим, если в убывающем порядке – вычитающим. Счетчики, у которых направление перебора кода может изменяться, называют реверсивными.
Рисунок 12
Различают счетчики синхронные и асинхронные. Если для работы счетчика требуется наличие синхросигнала, то такой счетчик называют синхронным. Счетчики, которые работают без синхросигналов, называют асинхронными.
Обобщенная схема счетчика приведена на рисунке 12. Счетчик СТ можно представить в общем случае как устройство, содержащее входную логику, управляющую работой счетчика, и выходную логику, которая используется для указания окончания счета или формирования сигнала переноса Р. Для приведения счетчика в начальное состояние (как правило – логические ноли на всех выходах) используется сигнал сброса, поступающий на вход R.

|
В некоторых типах счетчиков имеется возможность устанавливать исходное состояние отличным от нулевого. Параллельный код для предварительной установки счетчика поступает на входы s 0 ... Sn. Сигнал разрешения параллельной загрузки М останавливает счет и позволяет подготовленным на входах S 0 ... Sn данным загрузиться в счетчик в момент прихода очередного тактового импульса С. Счетчик считает тактовые импульсы, поступающие на вход С, если присутствует сигнал разрешения счета на входе V.
Выходными сигналами счетчика обычно являются сигналы, снимаемые с выходов отдельных разрядов Q 0 ... Qn, сигнал окончания счета или сигнал переноса – Р.
В качестве примера ниже приведены (рисунок 13) функциональная схема и условное графическое обозначение четырехразрядного асинхронного суммирующего счетчика К155ИЕ5. В таблице представлено назначение выводов счетчика.
Обозначение выводов 1 и 14 указывает на то, что изменение состояний счетчика происходит по перепаду входных импульсов от высокого к низкому уровню. ИМС К155ИЕ5 является аналогом ИМС 7493.

|
Рисунок 13
30) окальные сети. Понятие локальной сети и причины создания локальной сети. Основные понятия локальных сетей: сервер, файл-сервер, клиент, клиент-сервер, рабочая станция, ресурсы (информационные, аппаратные и программные). Особенности организации ЛС: одноранговая сеть (целесообразность применения, достоинства и недостатки), сеть с выделенным сервером(целесообразность применения, достоинства и недостатки). Топология локальных сетей. Понятие топологии сети и его характеристики. Основные топологии сетей: «звезда», «кольцо», «шина», а также достоинства и недостатки.
5.1. Понятие локальной сети и причины создания локальной сети. LAN (Local Area Network) – локальные сети, имеющие замкнутую инфраструктуру до выхода на поставщиков услуг. Термин «LAN» может описывать и маленькую офисную сеть, и сеть уровня большого завода, занимающего несколько сотен гектаров. Зарубежные источники дают даже близкую оценку – около шести миль (10 км) в радиусе; использование высокоскоростных каналов.
Преимущества сетевой связи:
§ разделение файлов. Сеть позволяет вам пользоваться общей информацией вместе с другими пользователями в сети. Существуют два способа доступа к информации. Первый способ - прямой доступ: от компьютера к компьютеру. Второй - через промежуточный пункт (сервер).
§ разделение ресурсов. Сеть позволяет пользоваться общими компьютерными ресурсами - например, диск или принтер.
§ разделение программ. Удобнее поместить используемую программу на общий диск, чем хранить на каждом диске.
5.2. Основные понятия локальных сетей: сервер, файл-сервер, клиент, клиент-сервер, рабочая станция, ресурсы (информационные, аппаратные и программные). Особенности организации ЛС: одноранговая сеть (целесообразность применения, достоинства и недостатки), сеть с выделенным сервером (целесообразность применения, достоинства и недостатки). По организации управления ЛВС делятся на сети с централизованным и децентрализованным управлением.
Сети с централизованным управлением (сеть типа Клиент/сервер). В сети Клиент/сервер каждый компьютер играет определенную роль: он может выступать как сервер или как клиент. Сервер предназначен для предоставления своих ресурсов всем клиентским компьютерам в сети. Остальные компьютеры в сети выступают в роли клиентов. Чаще всего сервер предназначен для выполнения определенных задач:
§ файловый сервер
§ сервер печати
§ факс-сервер
§ почтовый сервер и т.д.
Компьютер-клиент – это обычный РС с установленной операционной системой, который соединяется с сервером, а не с другими компьютерами ЛВС. Достоинства сети с выделенным сервером:
§ надежная система защиты информации;
§ высокое быстродействие;
§ отсутствие ограничений на число рабочих станций;
§ простота управления по сравнению с одноранговыми сетями
Недостатки сети:
§ высокая стоимость из-за выделения одного компьютера под сервер;
§ зависимость быстродействия и надежности сети от сервера;
§ меньшая гибкость по сравнению с одноранговой сетью.
Одноранговые сети. В одноранговых сетях нет выделенных серверов, функции управления сетью передаются по очереди от одной PC к другой. Рабочие станции имеют доступ к дискам и принтерам других PC. Преимущества одноранговых сетей:
§ Не требуют дополнительных расходов на серверы и необходимое ПО.
§ Просты в инсталляции.
§ Не требуют специальной должности администратора сети
§ Позволяют пользователям управлять разделением ресурсов
§ При работе не вынуждают полагаться на функционирование других компьютеров
§ Стоимость создания небольших сетей достаточно низка
Недостатки одноранговых сетей:
§ Дополнительная нагрузка на компьютеры из-за совместного использования ресурсов
§ Неспособность одноранговых узлов обслуживать большое число соединений
§ Отсутствие централизованной организации, что затрудняет поиск данных
§ Нет центрального места хранения файлов, что осложняет их архивирование
§ Необходимость администрирования пользователями собственных компьютеров
§ Слабая и неудобная система защиты
Отсутствие централизованного управления, осложняющее работу с большими одноранговыми сетями
Топология ЛВС — это усредненная геометрическая схема соединений узлов сети. Топологии вычислительных сетей могут быть самыми различными, но для локальных вычислительных сетей типичными являются всего три: кольцевая, шинная, звездообразная. Иногда для упрощения используют термины — кольцо, шина и звезда.
Кольцевая топология предусматривает соединение узлов сети замкнутой кривой — кабелем передающей среды (рис. 1). Выход одного узла сети соединяется с входом другого. Информация по кольцу передается от узла к узлу. Каждый промежуточный узел между передатчиком и приемником ретранслирует посланное сообщение. Принимающий узел распознает и получает только адресованные ему сообщения.
Шинная топологи я — одна из наиболее простых (рис. 2). Она связана с использованием в качестве передающей среды коаксиального кабеля. Данные от передающего узла сети распространяются по шине в обе стороны. Промежуточные узлы не транслируют поступающих сообщений. Информация поступает на все узлы, но принимает сообщение только тот, которому оно адресовано. Дисциплина обслуживания параллельная.
Звездообразная топология (рис. 3) базируется на концепции центрального узла, к которому подключаются периферийные узлы. Каждый периферийный узел имеет свою отдельную линию связи с центральным узлом. Вся информация передается через центральный узел, который ретранслирует, переключает и маршрутизирует информационные потоки в сети.
| Рис. 2. Сеть шинной топологии
| Рис. 3. Сеть звездообразной топологии
|
В реальных вычислительных сетях могут использоваться более сложные топологии, представляющие в некоторых случаях сочетания рассмотренных. Выбор той или иной топологии определяется областью применения ЛВС, географическим расположением ее узлов и размерностью сети в целом.
Существуют стандарты для ЛВС. Стандарт - это множество различных правил и приспособлений (сетевые платы, кабели, устройства), на которых должна быть построена ваша сеть. Стандарт Ethernet - наиболее распространенный стандарт для небольших сетей. Существуют еще две: Token Ring и ARCnet. Но Ethernet используется чаще, чем две другие системы, поскольку она намного дешевле первой и быстрей второй.
Управляют работой сети сетевые операционные системы (СОС). Самые распространенные СОС - Windows Server, Unix, Linux, NetWare, OS/2 и другие.
31) Из того, что протокол является соглашением, принятым двумя взаимодействующими объектами, в данном случае двумя работающими в сети компьютерами, совсем не следует, что он обязательно представляет собой стандарт. Но на практике при реализации сетей стремятся использовать стандартные протоколы. Это могут быть фирменные, национальные или международные стандарты.
Международная Организация по Стандартам (International Standards Organization, ISO) разработала модель, которая четко определяет различные уровни взаимодействия систем, дает им стандартные имена и указывает, какую работу должен делать каждый уровень. Эта модель называется моделью взаимодействия открытых систем (Open System Interconnection, OSI) или моделью ISO/OSI.
В модели OSI взаимодействие делится на семь уровней или слоев (рис. 1.1). Каждый уровень имеет дело с одним определенным аспектом взаимодействия. Таким образом, проблема взаимодействия декомпозирована на 7 частных проблем, каждая из которых может быть решена независимо от других. Каждый уровень поддерживает интерфейсы с выше- и нижележащими уровнями.

Рис. 1.1. Модель взаимодействия открытых систем ISO/OSI
Модель OSI описывает только системные средства взаимодействия, не касаясь приложений конечных пользователей. Приложения реализуют свои собственные протоколы взаимодействия, обращаясь к системным средствам. Следует иметь в виду, что приложение может взять на себя функции некоторых верхних уровней модели OSI, в таком случае, при необходимости межсетевого обмена оно обращается напрямую к системным средствам, выполняющим функции оставшихся нижних уровней модели OSI.
Приложение конечного пользователя может использовать системные средства взаимодействия не только для организации диалога с другим приложением, выполняющимся на другой машине, но и просто для получения услуг того или иного сетевого сервиса, например, доступа к удаленным файлам, получение почты или печати на разделяемом принтере.
Итак, пусть приложение обращается с запросом к прикладному уровню, например к файловому сервису. На основании этого запроса программное обеспечение прикладного уровня формирует сообщение стандартного формата, в которое помещает служебную информацию (заголовок) и, возможно, передаваемые данные. Затем это сообщение направляется представительному уровню. Представительный уровень добавляет к сообщению свой заголовок и передает результат вниз сеансовому уровню, который в свою очередь добавляет свой заголовок и т.д. Некоторые реализации протоколов предусматривают наличие в сообщении не только заголовка, но и концевика. Наконец, сообщение достигает самого низкого, физического уровня, который действительно передает его по линиям связи.
Когда сообщение по сети поступает на другую машину, оно последовательно перемещается вверх с уровня на уровень. Каждый уровень анализирует, обрабатывает и удаляет заголовок своего уровня, выполняет соответствующие данному уровню функции и передает сообщение вышележащему уровню.
Кроме термина "сообщение" (message) существуют и другие названия, используемые сетевыми специалистами для обозначения единицы обмена данными. В стандартах ISO для протоколов любого уровня используется такой термин как "протокольный блок данных" - Protocol Data Unit (PDU). Кроме этого, часто используются названия кадр (frame), пакет (packet), дейтаграмма (datagram).
Поиск по сайту: