ІІ. 2. Перший закон термодинаміки

Перший закон термодинаміки відомий зазвичай як окремий випадок закону збереження енергії в застосуванні до процесів, що супроводжуються виділенням, поглинанням або перетворенням її. Енергія, як відомо, може перетворюватись із однієї форми в іншу, але не може виникати або зникати. Повна енергія ізольованої системи стала. Цей закон встановлює зв’язок між кількістю теплоти, одержаної чи виділеної в процесі, кількістю виконаної або одержаної роботи і зміною внутрішньої енергії системи.

Якщо в ряді систем відбуваються кругові термодинамічні процеси і для кожного із них підрахований баланс теплоти Q і роботи W, то у відповідності з дослідом і незалежно від характеру процесу і природи системи

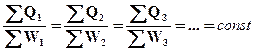, (ІІ.2.1)

де ∑Q _і – алгебраїчна сума теплот всіх процесів, що протікають в і -тій системі; ∑W _і – алгебраїчна сума всіх робіт, що виконуються і -тою системою проти всіх діючих на неї сил (тиск, електрорушійна сила і ін.); const – механічний еквівалент теплоти; при однакових одиницях вимірюваннях теплоти і роботи він рівний одиниці.

Рівняння (ІІ.2.1) встановлює еквівалентність теплоти і роботи. Теплоту і роботу в циклічному процесі доцільно записати як суму (інтеграл) безкінечно малих (елементарних) теплот dQ і безкінечно малих (елементарних) робіт dW, при цьому межа початкового і кінцевого інтегрувань співпадають (цикл).

Домовимось, як уже зазначалось вище, вважати позитивними теплоту, що одержується системою від навколишнього середовища, і роботу, що виконується системою. Тоді еквівалентність теплоти і роботи в циклічному процесі можна записати так:

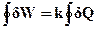, (ІІ.2.2)

де 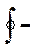означає інтегрування за циклом; k – механічний еквівалент теплоти.

Для не кругового процесу рівність (ІІ.2.2) не зберігається, оскільки система не повертається у вихідний стан. Замість цієї рівності для не кругового процесу можна записати (випускаючи коефіцієнт k):

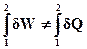(ІІ.2.3)

Оскільки межі інтегрування в загальному випадку довільні, то і для елементарних величин dW і dQ:

dQ – dW ¹ 0 (ІІ.2.4)

Позначимо різницю dQ – dW для будь-якого елементарного термодинамічного процесу через dU

dU º dQ – dW (ІІ.2.5)

і для кінцевого процесу

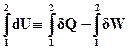(ІІ.2.6)

Повертаючись до кругового процесу, у відповідності з рівнянням (ІІ,2.1)

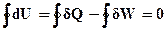(ІІ.2.7)

Таким чином, величина dU є повним диференціалом деякої функції стану системи, і при поверненні системи до вихідного стану (після циклічної зміни) величина цієї функції набуває початкового значення. Функція стану системи U, що визначається рівняннями (ІІ.2.5), (ІІ.2.6), як уже було розглянуто вище, називається внутрішньою енергією системи. Очевидно, вираз (ІІ.2.6) можна записати і так:

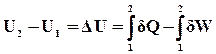(ІІ.2.8)

Якщо система здійснює який-небудь конкретний процес, внаслідок чого вона переходить із одного стану (початкового) в інший (кінечний) і виконує при цьому зовнішню роботу W, одержуючи в той же час від зовнішнього середовища теплоту Q, то різницю Q–W називають приростом внутрішньої енергії системи DU в даному процесі:

DU = Q – W (ІІ.2.9)

Таким чином, приріст внутрішньої енергії (DU) не залежить від шляху, по якому система перейшла із початкового стану в конечний, тобто не залежить від того, з допомогою якого саме процесу із багатьох можливих відбувся цей перехід.

Хоч кожному такому процесу відповідають свої значення Q і W, різниця їх DU залишається однією і тією ж для будь-якого шляху переходу. Це значить, що енергія є однозначною функцією стану системи і має в кожному стані системи цілком певне значення.

Так як енергія U є функцією стану то ми можемо вести мову про,,запас“ її в кожному даному стані системи, теплота Q і робота W не є такими і мають сенс характеристик конкретного процесу.

Для безкінечно малої зміни стану системи рівняння (ІІ.2.9) прийме вигляд

dU = dQ – dW = dQ – (pdV + dW¢), (ІІ.2.10)

де dW – сума всіх елементарних робіт, тобто в загальному випадку роботи pdV на подолання зовнішнього тиску і роботи dW¢ проти електричних, магнітних і ін. сил (так званої корисної роботи).

Рівняння (ІІ.2.9) і (ІІ.2.10) є математичними виразами першого закону термодинаміки. А закон можна сформулювати так:

В будь-якому процесі приріст внутрішньої енергії DU якої-небудь системи рівний кількості наданої системі теплоти Q мінус кількість роботи W, що здійснюється системою.

Якщо система знаходиться під певним зовнішнім тиском, а інші сили відсутні або їх впливом можна знехтувати, то (ІІ.2.10) приймає вигляд

dU = dQ – pdV (ІІ.2.11)

Оскільки у більшості випадків хімічні процеси протікають при сталому зовнішньому тиску і при відсутності яких-небудь інших дій на систему, то для їх описання застосовують саме це рівняння. Для таких систем єдиним видом роботи є робота розширення. Практичне значення має робота розширення газу. Багато реальних газів при досить низьких тисках і порівняно високих температурах наближено підкоряються законам ідеальних газів. Розглянемо математичні співвідношення для обчислення роботи розширення ідеального газу в різних процесах.

У залежності від умов і форм ведення процесу кількість роботи при даній зміні об’єму, наприклад, від V₁ до V₂, може бути різною в межах від нуля до деякої кінечної величини. При розширенні газу в пустоту він не долає ніякого опору і, також, ніяка робота не виконується (W = 0). Чим більший опір приходиться долати газові при розширенні, тим більшу роботу він виконує. Максимальну роботу (W_м) газ виконує тоді, коли процес відбувається оборотно. Розглянемо оборотне розширення газу, що відбувається в циліндрі сталого перетину S. Зробимо припущення, що поршень рухається без тертя і, долаючи зовнішній тиск р, зміщується на малу величину висоти циліндра dh. Робота, яка при цьому виконується, визначатиметься:

dW_м = р×S×dh (ІІ.2.12)

або, оскільки Sdh рівна зміні об’єму dV

dW_м = р×dV (ІІ.2.13)

і для зміни об’єму від V₁ до V₂:

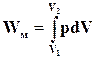(ІІ.2.14)

При розширенні газу чи пари V₂>V₁, робота виконується проти зовнішнього тиску. Проте робота може виконуватись і над системою, при цьому V₂<V₁ і знак в рівнянні (ІІ.2.14) змінюється на протилежний.

Для розв’язання рівняння (ІІ.2.14) необхідно знати залежність тиску від об’єму, тобто рівняння стану газу. Ця залежність для ідеального газу описується рівнянням стану Клапейрона-Менделєєва:

р×V = nRT (ІІ.2.15)

Розглянемо вирази для максимальної роботи розширення ідеального газу в п’яти процесах: ізобарному, ізотермічному, адіабатичному, ізохорному й ізобарно-ізотермічному.

1. Ізобаричний процес відповідає умові сталості тиску (р = const). У цьому випадку інтегрування рівняння (ІІ.2.13) дає вираз

W_м = р(V₂ – V₁) (ІІ.2.16)

На графіку (рис. 4) цій роботі відповідає площа прямокутника V₁EFV₂. Скориставшись рівнянням (ІІ.2.15) і враховуючи, що рV₂=nRT₂, а рV₁=nRT₁, будемо мати

W_м = nR(T₂ – T₁) (ІІ.2.17)

2. Ізотермічний процес відповідає умові сталості температури (Т= const). Розглядаючи розширення n молів газу і підставляючи в рівняння (ІІ.2.14) замість р величину 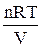із (ІІ.2.15), одержуємо

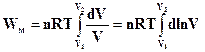
Після інтегрування цього рівняння матимемо

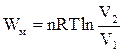(ІІ.2.18)

Враховуючи, що при сталій температурі тиск обернено пропорційний об’єму (р₁V₁ = р₂V₂), рівнянню (ІІ.2.18) можна надати такий вигляд:

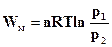(ІІ.2.19)

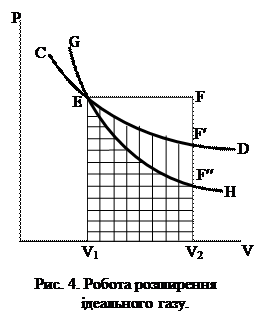Графічно (рис. 4) ізотермічний процес, зображений кривою СD, а розглядувана робота – площа V₁EF¢V₂.

3. Якщо протікає адіабатичний процес, то одночасно змінюються температура і тиск. У зв’язку з тим, що газ не одержує енергії ззовні, робота адіабатичного розширення виконується за рахунок внутрішньої енергії, тобто Q = 0 і газ охолоджується:

W_м = – DU (ІІ.2.20)

Рівняння першого закону (ІІ.2.11) для цього процесу запишеться

dU + dW = 0 (ІІ.2.21)

або

dW = - dU = pdV, (ІІ.2.22)

тобто, робота буде здійснюватись за рахунок зменшення внутрішньої енергії газу, який повинен охолоджуватись.

Знайдемо зв’язок між об’ємом і тиском в адіабатному процесі. Відомо, що dU = C_vdT, де C_v - теплоємність при сталому об’ємі. Скориставшись рівнянням (ІІ.2.22) отримаємо

C_vdT + pdV = 0 (ІІ.2.23)

В цьому рівнянні замінемо р з рівняння стану ідеального газу і розділимо його на Т:

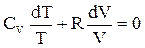(ІІ.2.24)

В цьому рівнянні розділені змінні, і його можна інтегрувати наближено вважаючи, що C_v від температури не залежить:

C_v lnT + R lnV = const, (ІІ.2.25)

де const - стала інтегрування. Або, об’єднуючи логарифми,

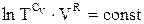. (ІІ.2.26)

Якщо логарифм є сталою величиною, то і підлогарифмічна функція, тобто

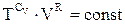. (ІІ.2.27)

Це і є одна із форм рівняння адіабати, що зв’язує об’єм і температуру газу. Заміняючи температуру з рівняння ідеального газу, запишем

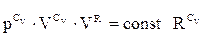. (ІІ.2.28)

Об’єднавши степені об’єму, взявши корені степені C_v та включивши R в загальну сталу отримаємо:

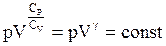, (ІІ.2.29)

де g - відношення теплоємностей при сталих тиску і об’єму; g > 1.

Виведемо формулу для обчислення роботи адіабатного процесу. Підставимо тиск із (ІІ.2.29) в інтеграл роботи (ІІ.2.14), тоді

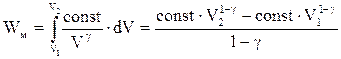. (ІІ.2.30)

Але у відповідності (ІІ.2.29) 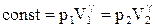, тому, перетворюючи (ІІ.2.30), отримаємо рівняння

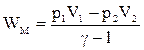, (ІІ.2.31)

яке є виразом для роботи адіабатного процесу через початкові і кінечні значення тиску і об’єму. Якщо скористатись рівнянням стану ідеального газу для n моль, то (ІІ.2.31) можна подати в такому вигляді:

W_м = nC_v(T₁ - T₂). (ІІ.2.32)

З цього видно, що адіабатна робота пропорційна різниці температур.

Графічно (рис. 4) адіабатичний процес подано кривою GH, а розглядувана робота – площею V₁EF¢¢V₂.

Крім рівняння (ІІ.2.27) роботу можна визначити і за такими рівняннями:

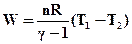; (ІІ.2.33)

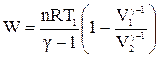; (ІІ.2.34)

де V₁ i V₂ – початковий і кінечний об’єми; Т₁ і Т₂ – початкова і кінечна температури.

4. Ізохоричний процес відповідає умові сталості об’єму (V = const). Із рівняння (ІІ.2.14) одержуємо, що W_м = 0.

5. Ізобарно-ізотермічний процес відповідає умові, коли р = const і Т = const. Якщо число молів n в суміші змінюється внаслідок хімічної реакції, наприклад:

2СО + О₂ = 2СО₂, N₂O₄ = 2NO₂,

або внаслідок фізичного процесу, наприклад при випаровуванні рідини, то протікає ізобарно-ізотермічний процес розширення або стискування суміші газів. При цьому максимальна робота розширення ідеального газу у відповідності з рівнянням (ІІ.2.16) буде рівна

W_м = р(V₂ – V₁) = рDV(ІІ.2.35)

При р = const і Т = const із рівняння (ІІ.2.15) одержуємо

рDV = DnRT, (ІІ.2.36)

звідки

W_м = DnRT, (ІІ.2.37)

Поиск по сайту: