 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Отношения несовместимости
Соподчиненность Противоположность Противоречие





 |
С
4. В практике мышления мы часто пользуемся логическими приемами обобщения и ограничения понятия. Обобщить понятие — значит расширить его объем, т.е. путем исключения ряда признаков отраженных в понятии предметов перейти от понятия с меньшим объемом, но более определенным содержанием. Это необходимо тогда, когда мы стремимся вскрыть в предметах общие их признаки и определить законы, по которым они существуют и взаимодействуют с другими предметами. Примером обобщения является переход от понятия «персональный компьютер» к понятию «компьютер». Предельным обобщением выступают наиболее общие понятия – универсалии. Ограничить понятие – значит, напротив, сузить его объем за счет введения в него новых уточняющих признаков, последовательно переходя от родового понятия к видовому, затем подвидовому и т.д. Примером такой логической операции может служить переход от понятия «документ» к понятию «документ, имеющий юридическую силу».
В практике наших рассуждений и дискуссий огромное значение имеет не только уточнение объемов понятий, но также четкое понимание и фиксирование содержания употребляемых понятий. Несоблюдение этого требования может вести к серьезным заблуждениям и даже к сознательному искажению истины в угоду чьим-либо субъективным целям и интересам. Дело в том, что содержание понятия, особенно если оно достаточно сложное и не является общепринятым, часто не обнаруживается сразу и непосредственно в выражающем его термине. Поэтому каждый термин, особенно в науке, прежде чем употреблять его в качестве элемента обоснования каких-либо положений и выводов, требуется точно и четко определить.
Определение понятия (дефиниция[5]) − это логическая операция, раскрывающая содержание понятия, либо устанавливающая значение термина.
Определения бывают реальные [6] и номинальные [7].
Реальным называется определение, в котором раскрываются существенные и отличительные признаки самого предмета. Например: «Электродвигатель – это машина, преобразующая электрическую энергию в механическую»; «Квадрат – это прямоугольник, все стороны которого равны». Реальное определение как бы завершает логическое формирование понятия и в этом смысле является определенным итогом изучения предмета, отраженного в нем.
Номинальным называется определение, посредством которого определяется не сам предмет, о котором идет речь, а обозначающий его термин (имя), либо вводится новый термин взамен описания какого-либо предмета. В номинальных определениях часто употребляются слова «называют», «означает» и им подобные. Например: «Термин «философия» в переводе с греческого означает «любовь к мудрости»»; «Область науки, изучающая процессы управления в органических и неорганических системах, называется кибернетикой».
Определение понятия производится, как правило, через другое (более широкое) понятие. В связи с этим различают определяемые и определяющие понятия. Чаше всего они находятся между собой в соотношении вида и рода, ближайшего к данному виду. К примеру, параллелограмм в геометрии определяется как четырехугольник, у которого противоположные стороны равны и параллельны. В определяющем (родовом) понятии всегда содержится указание на видовое отличие определяемого понятия. Символически все это может быть записано следующим образом:
А = В с,
где А – определяемое понятие; В – определяющее понятие; с – видовое отличие.
Однако бывают случаи, когда определить понятие подобным образом оказывается невозможным. Так бывает, когда надо определить понятие, которое нельзя подвести под еще более широкое понятие. Тогда единственным выходом оказывается раскрытие содержания понятия через установление его соотношения с другим столь же широким понятием. Так определяется, например, в материалистической философии понятие «материя» через установление такого ее признака, как первичность по отношению к сознанию.
Наряду с определением понятия существуют другие приемы, сходные с ним, но не раскрывающие в достаточной степени содержание понятия. К ним относятся: описание, т.е. перечисление ряда внешних, хотя и важных для предмета признаков; характеристика, т. е. перечисление некоторых как внутренних и существенных признаков предмета; разъяснение посредством примеров или сравнения предмета с другими предметами, не находящимися с данным предметом в родовидовом отношении.
Эти приемы часто используют (в том числе и в сочетании друг с другом), когда затрудняются дать четкое и точное определение предмета. Следует, однако, иметь в виду, что, несмотря на определенную пользу, ни один из указанных приемов и даже все они, взятые вместе, не могут в полной мере заменить определения.
Определение понятия должно опираться на ряд правил, соблюдение которых позволяет избежать серьезных логических ошибок.
1. Определение должно быть понятным и, по возможности, кратким. Слишком многословное определение запутывает смысловое значение понятия, делает его недостаточно ясным для понимания. В определении также не должны применяться расплывчатые или двусмысленные термины, образные сравнения, метафоры и т.п.
2. Определение должно быть соразмерным. Это значит, что объем определяемого понятия (А) должен быть равным объему определяющего его понятия (В с). Нарушение этого правила приводит к следующим логическим ошибкам:
а) широкое определение, когда определяющее понятие шире определяемого (А < В с). Например: «Автомобиль – это техническое средство, предназначенное для перемещения людей и грузов и приводимое в движение двигателем внутреннего сгорания». В этом случае под понятие «автомобиль» попадают и мотоцикл, и тепловоз и ряд других транспортных средств.
б) узкое определение, когда, напротив, определяющее понятие уже определяемого (А > В с). Например: «Завод – это промышленное предприятие, выпускающее технические средства». Здесь, как видим, в понятие «завод» оказываются не включенными предприятия по переработке продукции, скажем, сельскохозяйственной;
в ) определение широкое в одном отношении и узкое в другом. Например: «Бочка – сосуд для хранения жидкостей». С одной стороны, это широкое определение, поскольку хранить жидкости можно и в цистерне, и в термосе, и в банке. С другой стороны, это узкое определение, так как бочка пригодна для хранения не только жидкостей, но и сыпучих материалов.
3. Определение не должно содержать тавтологии [8] и так называемого «порочного круга». Это значит, что недопустимо определять понятие через само это понятие или посредством указания на признак, зависимый от самого этого понятия. Например, нельзя определять преступника как человека, совершившего преступление, или масло как маслянистый предмет. Порочный круг возникает тогда, когда в начале понятие определяется через какое-то другое понятие, а затем само это (определяющее) понятие определяется через понятие, которое вначале было определяемым. Например, вращение определяется как движение тела вокруг своей оси, а затем ось определяется как прямая, вокруг которой осуществляется вращение тела.
4. Определение не должно быть исключительно отрицательным. Если отрицание и содержится в определении, то оно должно быть лишь вспомогательным звеном, ведущим к утверждению основных признаков предмета или класса предметов и тем самым раскрытию содержания определяемого понятия.
Наряду с определением понятий, большое значение для логической стройности и аргументированности рассуждений имеют логическая операция деления понятий. Деление понятия – логическая операция, раскрывающая объем понятия путем вычленения в нем более узких (видовых) классов. В структуре логического деления различают делимое понятие, объем которого следует раскрыть, и члены деления, т. е. соподчиненные делимому понятию видовые понятия. Например, деление понятия «поезд» предполагает вычленение в нем таких классов (видов): «пассажирский поезд» и «грузовой поезд». Возможно деление этого понятия и на другие классы, к примеру: «пригородный поезд» и «поезд дальнего следования». Все дело в том, по какому основанию осуществляется деление понятия. Основанием деления в логике называется признак, по которому внутри более широких (родовых) понятий производится вычленение более узких (видовых). К операции деления понятий нам приходится прибегать очень часто, поскольку эта операция позволяет через уточнение объема понятия углубить его содержание и тем самым сделать его более определенным.
От логического деления понятий нужно отличать мысленное расчленение самого предмета, отраженного в понятии, на его составные части. Например, реальный железнодорожный путь можно, в том числе и мысленно, расчленить на рельсы, шпалы, стрелочные переводы и т.д. В результате же логического деления понятия «железнодорожный путь» мы получаем понятия «железнодорожный путь с нормальной шириной колеи» и «узкоколейный железнодорожный путь».
Для выполнения логической операции деления понятия необходимо соблюдать ряд правил, нарушение которых с неизбежностью ведет к ошибкам и заблуждениям.
1. Деление должно быть соразмерным. Это значит, что объем делимого понятия должен быть равен суммарному объему членов деления. Иначе говоря, нельзя допускать таких логических ошибок, как неполное деление (когда в члены деления родового понятия включаются не все видовые понятия, которые могут быть выделены по выбранному основанию), и деление с лишними членами. Примером первой ошибки является такое деление: «Энергия в физике делится на механическую, тепловую и электрическую». В этом случае за пределами понятия «энергия» необоснованно остаются атомная энергия, энергия ядерных взаимодействий и др. Тем самым объем делимого понятия «энергия» становится шире, чем сумма членов произведенного деления. Примером другой ошибки является такая фраза: «Химические элементы делятся на металлы, неметаллы и сплавы». Лишним членом здесь является понятие «сплавы», т. к. отраженный в нем предмет не относится к классу химических элементов.
2. Деление должно производиться по единому основанию. Несоблюдение этого правила ведет к перекрещиванию понятий и, в конечном счете, к путанице и серьезным ошибкам в аргументации. Так, например, нарушением этого правила будет деление родового понятия «транспорт» сразу на такие видовые понятия, как «железнодорожный транспорт», «авиационный транспорт», «наземный транспорт», «электрический транспорт».
3. Деление должно быть последовательным. Это значит, что не допускаются скачки в делении, т.е. все члены деления должны быть ближайшими видами делимого родового понятия. Иначе говоря, нельзя выделять из родового понятия сразу подвидовые, минуя видовые. Неверно, например, деление литературы на художественную, научно-техническую, учебную, публицистическую, прозаическую и поэтическую. Правильным будет вначале разделить литературу на художественную, научно-техническую, учебную и публицистическую, а затем уже художественную литературу – на поэтическую и прозаическую.
Деление понятий служит логической основой для осуществления классификации. Классификация − это распределение предметов по классам, где каждый класс имеет постоянное строго определенное место.
Классификация является одним из важнейших моментов научного познания. Очень важен при этом выбор основания классификации. Она может производиться по существенным (естественная) и несущественным (вспомогательная) признакам. Примером естественной классификации является периодическая таблица Д.И. Менделеева, примерами вспомогательной – любой словарь, предметный или поименный указатели в научной монографии и т.п.
Лекция 3. СУЖДЕНИЕ
1. Суждение как логическая форма, его структура и языковое выражение.
2. Классификация суждений и условия истинности сложных суждений.
3. Отношения между суждениями и «Логический квадрат».
4. Определение истинности суждений в их отношениях.
1. Познание мира предполагает не только чувственное, а затем мысленно-понятийное выделение предметов, но и их сопоставление, сравнение друг с другом с установлением их сходства и различия. Содержание опыта становится знанием, когда этот опыт осмысливается и принимает форму высказывания, говоря языком логики, – суждения. Суждением называется логическая форма, в которой что-либо утверждается или отрицается о предмете мысли, его существовании, свойствах или отношениях c другими предметами. Назначение суждения – отразить действительность такой, какова она есть, а логическая его функция состоит в том, чтобы, сопоставляя одно понятие с другими, судить (отсюда и название) о предметах реального мира.
С суждения начинается подлинный акт мысли. Если понятием выражается предметный характер нашего мышления, то суждением раскрывается активное отношение мысли к действительности. Как форма мысли суждение более сложно в структурном плане, чем понятие, хотя их формирование всегда взаимообусловлено.
В структуре суждения выделяют в качестве обязательных три элемента – субъект (S), предикат (Р) и связку. Субъектом суждения называется понятие о предмете мысли, предикатом суждения – понятие о его существовании, свойствах и отношениях. Объект и предикат называются терминами суждения. Отношение между предметом мысли и его свойствами и связями с другими предметами выражаются связкой («есть», «не есть»). Если попытаться выразить структуру суждения в самом общем виде, то она может быть представлена формулой: «S есть (не есть) Р».
В языке суждения выражаются чаще всего повествовательными предложениями, например: «Роза есть цветок», «Буря мглою небо кроет» и т.п. Иногда перед субъектом суждения стоят такие слова («все», «ни один из», «некоторые» и т.п.), которые уточняют его объем. Такие слова в логике принято называть кванторами. Например: «Ни один дельфин не является рыбой»; «Многие студенты получают повышенную стипендию».
Достаточно часто встречаются суждения, в которых субъект выражен не явно, но, тем не менее, всегда предполагается. В языке такие суждения принимают форму безличных предложений («Светает»; «Знобит»; «Подтаяло»). Не выражают никаких суждений вопросительные предложения и многие побудительные предложения («Берегите леса»; «Зри в корень!» и т.п.). Ряд побудительных предложений, в частности те, в которых сформулированы приказы («В атаку!»; «Ни шагу назад!»), а также призывы или лозунги («Берегите мир!»; «Люби ближнего своего!» и т. п.) хотя и выражают суждения, но суждения особого модального типа, которые выходят за рамки нашего рассмотрения в силу ограниченного объема учебного курса логики в техническом вузе.
2. Для уяснения сущности суждения и его роли в познании большое значение имеет классификация суждений. Прежде всего, все суждения могут быть подразделены на простые и сложные (состоящие из двух и более простых). Начнем рассмотрение вопроса с простых суждений, поскольку, разобравшись с ними, не столь трудно будет уяснить и все, что касается сложных.
Простые суждения классифицируют соответственно их структурным особенностям на виды и разновидности по следующим основаниям:
а) по содержанию предиката. По этому основанию все суждения подразделяются на суждения существования, атрибутивные суждения и суждения отношения.
Суждения существования (экзистенциальные) решают вопрос о наличии или отсутствии предмета мысли. Примерами таких суждений являются: «Не существует беспричинных явлений»; «В городском парке стоит шахматный павильон».
Суждения свойства (атрибутивные) дают знание о свойствах предмета либо о принадлежности его к какому-нибудь классу предметов, например: «Роза имеет приятный запах»; «Факультет является важнейшим структурным подразделением вуза».
Суждения отношения (реляционные), как видно из самого названия, выражают различные отношения между предметами (по месторасположению, по времени, по причинной обусловленности и т.д.). К ним относятся, к примеру, такие суждения: «Волга длиннее, чем Дон»; «Протон тяжелее электрона»; «Цвет хамелеона зависит от окраса той среды, в которой он находится».
б) по качеству связки. Основанием деления здесь является основная логическая функция суждения: утверждение или отрицание чего-либо. По такому основанию все суждения подразделяются на утвердительные и отрицательные, соответственно тому, каков тип связки («есть» или «не есть»). Пример утвердительного суждения: «Безотходные технологии позволяют экономить сырье и энергию». Пример отрицательного суждения: «Ни один из существующих двигателей внутреннего сгорания не является абсолютно экологически чистым».
в) по объему субъекта выделяют: единичное суждение, субъект которого включает только один предмет, частное суждение, в котором объем субъекта включает часть какого-либо класса предметов, и общее суждение, где объем субъекта – весь класс предметов. Так, суждение «Сергей Есенин – великий русский поэт» представляет собой единичное суждение, суждение «Некоторые металлы не тонут в воде» является частным, а суждение «Все студенты технических вузов изучают высшую математику» – общим. Разновидностями деления суждений по объему субъекта являются исключающие, которые по смыслу выступают как частные, а по форме как общие («Все студенты, за исключением больных, пришли на семинар по логике»), и выделяющие, в состав которых входят кванторы «только», «исключительно» и им подобные («Только добрый человек может быть хорошим врачом»).
Учитывая особую значимость количественных (по объему субъекта) и качественных (по качеству связки) характеристик суждений, в логике выработана также их единая количественно-качественная классификация и соответствующая ей символика: А – общеутвердительное суждение; Е – общеотрицательное суждение; I – частноутвердительное суждение; О – частноотрицательное суждение. Эта символика позволяет дать наглядное представление об отношениях между суждениями с помощью так называемого «логического квадрата», о чем речь пойдет ниже.
г) по модальности. Здесь основанием для деления суждений выступает степень достоверности выраженного в них знания. По этому показателю выделяются: суждения возможности (проблематические), выражающие неполноту наших знаний («Возможно, все студенты группы сдадут экзамен по физике»; «Вероятно, он был болен»); суждения действительности, констатирующие наличие или отсутствие у предмета того либо иного свойства, качества («Современная НТР характеризуется высоким уровнем компьютеризации научного познания, обучения и производственной деятельности»), суждения необходимости, которые выражают обязательность указанной в них связи между субъектом и предикатом («Необходимым условием становления специалиста является его самообразование»). Важно при этом иметь в виду, что различение суждений по данному основанию определяется объективными характеристиками предметов, а не субъективными желаниями человека.
Следует отметить, что в логических операциях с суждениями часто бывает необходимо установить распределенность входящих в их структуру терминов – субъекта и предиката. Термин считается распредленным, если он взят в суждении в полном объеме, т.е. охватывает весь класс предметов, отраженных в нем. Если же термин охватывает лишь часть этого класса предметов, то он считается нераспределенным. Символически распределенность и нераспределенность терминов принято обозначать знаками «+» и «–». Например, в суждении «Все граждане нашей страны (S +) имеют право на образование (P ‾)» субъект распределен, а предикат – не распределен, т.к. мыслится не в полном объеме граждан, имеющих право на образование, а ограничен в данном случае только гражданами нашей страны.
Для облегчения определения распределенности терминов можно использовать выработанные в логике следующие правила:
1. В общеутвердительных суждениях субъект всегда распределен, а предикат не распределен (исключением являются выделяющие суждения, где субъект и предикат равны в своих объемах и потому предикат также распределен).
2. В частноутвердительных суждениях субъект и предикат находятся в отношении перекрещивания и потому оба взяты не в полном объеме (исключение составляют опять же выделяющие суждения, в которых субъект не распределен, а предикат распределен).
3. В общеотрицательных суждениях и субъект, и предикат распределены.
4. В частноотрицательных суждениях субъект не распределен, а предикат распределен.
Указанные правила представлены в следующей таблице:
| Вид суждения Термины суждения | А | I | E | O |
| С Субъект (S) | + | – | + | – |
| П Предикат (P) | – | – | + | + |
| П Предикат выделяющих суждений | + | + | + | + |
Из таблицы можно вывести следующие закономерности: субъект всегда распределен в общих суждениях и нераспределен в частных; предикат распределен в отрицательных суждениях и не распределен в утвердительных; в выделяющих суждениях предикат всегда распределен.
Приведенная выше классификация относится, прежде всего, к простым суждениям. Для сложных же суждений в логике существует еще одно основание деления – по типу логических союзов, объединяющих ряд простых суждений в сложное. По этому основанию сложные суждения делятся на категорические, разделительные и условные.
Категорическое суждение, как видно из названия, выражает принадлежность или не принадлежность того или иного признака субъекту независимо от каких-либо условий (например: «Все в мире подвержено изменениям»; «Все вещества состоят из атомов»). Категорические суждения бывают как простые, так и сложные, состоящие из ряда простых суждений. Сложное категорическое суждение, в котором субъект либо предикат состоит из нескольких понятий, соединенных союзами «и» (в положительных суждениях) или «ни» (в отрицательных суждениях), называется соединительным или конъюнктивным [9] («Растительный и животный мир принадлежат живой природе»; «Ни Петрова, ни Сидорова не было в это время в Ростове»). Формула конъюнкции в символическом виде выглядит следующим образом: а 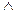 b, где буквы а и b обозначают простые суждения, а знак
b, где буквы а и b обозначают простые суждения, а знак 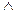 – символ союзов «и» либо «ни».
– символ союзов «и» либо «ни».
Разделительное или дизъюнктивное [10] суждение образуется из простых категорических суждений, соединенных союзами «или» и «либо», символом которых выступает знак 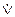 . Формула такого суждения: а
. Формула такого суждения: а  b. Значок «
b. Значок «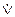 » означает строгость дизъюнкции, т. е. невозможность одновременного существования содержащихся в таком суждении альтернатив (например: «Завтра судебное заседание состоится или будет вновь отложено»).
» означает строгость дизъюнкции, т. е. невозможность одновременного существования содержащихся в таком суждении альтернатив (например: «Завтра судебное заседание состоится или будет вновь отложено»).
Однако иногда дизъюнктивное по своей форме суждение может по содержанию быть разделительно-соединительным, т.е. допускать возможность одновременного существования признаков предмета или событий, о которых идет речь в составляющих дизъюнкцию простых суждениях (например: «Успеха в спорте можно добиться либо благодаря природной одаренности, либо благодаря упорным тренировкам»). Такая дизъюнкция получила название нестрогой и в ее формуле точка над знаком дизъюнкции не ставится.
Условным или импликативным [11] называется такое сложное суждение, в котором простые суждения тесно связаны между собой условной зависимостью. Эта связь выражается логическим союзом «если..., то». Первое высказывание, в условном суждении, в котором выражено условие, называется основанием, а второе, зависимое от первого, – следствием. Примеры таких суждений: «Если через медную проволоку проходит электроток, то она нагревается»; «Если будет хорошая погода, то мы пойдем на пляж». Схема условного (импликативного) суждения: а  b, где знак
b, где знак  служит символом импликации.
служит символом импликации.
Условное суждение имеет три разновидности: суждение о причинной связи («Если придать радиоактивному веществу критическую массу, то произойдет атомный взрыв»); суждение о логическом основании («Если строго следовать законам логики, то результат рассуждений будет истинным»); суждение об условии («Если знаешь свое дело, то достигнешь необходимого результата»). Одним из подвидов последней разновидности является так называемое суждение эквиваленции [12]. Логической формой такого суждения выступает соединение двух высказываний связкой «если и только если..., то», либо «тогда и только тогда, когда». Символом такого типа связки выступает знак 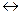 , а логическая формула приобретает вид: а
, а логическая формула приобретает вид: а 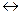 b.
b.
Для суждений конъюнкции, строгой и нестрогой дизъюнкции, импликации и эквиваленции в логике разработаны таблицы их истинности (в зависимости от истинности или ложности входящих в них простых суждений, получивших в логике название пропозициональных переменных). Если таблицы для всех видов сложных суждений соединить в одну, то она получит следующий вид:
| а | b | Конъюнкция
а 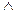 b b
| Дизъюнкция
(строгая)
а 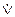 b b
| Дизъюнкция (нестрогая)
а 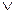 b b
| Импликация
а  b b
| Эквиваленция
а 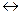 b b
|
| и и | и | и | л | и | и | и |
| и | л | л | и | и | л | л |
| л | и | л | и | и | и | л |
| л | л | л | л | л | и | и |
Примечание: буква «и» означает истинность суждения, а буква «л» – его ложность. Зачастую (например, в математической логике) истинность обозначается как 1, а ложность как 0.
Используя приведенную выше таблицу, можно проводить логический анализ и оценку (с позиций истинности, ложности или неопределенности) высказываний, включающих в себя ряд сложных суждений. Рассмотрим для примера следующее высказывание: «Если завтра будет солнечно, то мы хорошо покупаемся и позагораем». Логическая формула данного высказывания примет вид:
а → (b 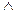 с)
с)
Для определения истинности данного высказывания для всех возможных значениях пропозиционных переменных составим соответствующую таблицу. В этой таблице количество строк для значений истинности пропозиционных переменных вычисляется по формуле 2n, где n равно числу пропозиционных переменных (в данном случае 23 = 8), а количество столбцов равняется сумме числа пропозиционных переменных и всех выполняемых выраженных в высказывании символами типовых логических союзов. При этом порядок проведения логических операций совпадает с порядком математических вычислений: вначале выполняются действия в скобках. Итоговая логическая операция (в нашем случае – дизъюнкция) записывается в последнем столбце.
| a | b | c | (b 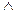 c) c)
| a  (b (b 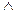 c) c)
|
| и | и | и | и | и |
| и | и | л | л | л |
| и | л | и | л | л |
| и | л | л | л | л |
| л | и | и | и | и |
| л | и | л | л | и |
| л | л | и | л | и |
| л | л | л | л | и |
Как мы видим, данное сложное высказывание в одних случаях принимает значение «истинно», а в других – «ложно». Такие высказывания в логике получили название выполнимых, или случайно истинных. Если высказывание во всех случаях оказывается истинным, оно называется общезначимым, или тождественно-истинным. Когда же высказывание всегда оказывается ложным, его называют логически-противоречивыми, или тождественно-ложными.
Однако метод составления полных таблиц истинности излишне громоздок. Так, к примеру, при четырех пропозиционых переменных в таблице будет 16 строк, при пяти – уже 32 и т. д. Таблица значительно разрастается и вширь при усилении сложности высказывания за счет увеличения числа логических операций в нем. Поэтому, учитывая, что в подавляющем большинстве случаев необходимо лишь однозначно определить, является ли высказывание общезначимым или нет, в логике выработан метод сокращенных таблиц. Проиллюстрируем его на примере сложного высказывания, разбирая ход рассуждений по последовательным шагам. Пусть нам дана формула высказывания следующего вида:
((a 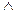 b)
b)  c)
c)  (a
(a  (b
(b 
 ))
))
1) Используя способ рассуждения «от противного», начинаем с предположения, что данная формула, являющаяся импликацией, не является истинной, т.е. на выходе имеет значение «ложь». Запишем это следующим образом:
((a 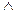 b)
b)  c)
c)  (a
(a  (b
(b 
 ))
))
л
2) Известно, что импликация дает значение «ложь» только при условии, когда ее основание является истинным, а следствие – ложным. В соответствии с этим запишем:
((a 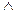 b)
b)  c)
c)  (a
(a  (b
(b 
 ))
))
л
и л
3) Теперь рассмотрим следствие нашего импликационного высказывания, т. к. анализ его основания затруднен, поскольку оно является истинной импликацией, что может быть не в одном, а в трех случаях. Определенная же выше ложность же следствия, которое также является импликацией, позволяет определить, что у него, в свою очередь, основание должно быть истинным, а следствие – ложным. Зафиксируем это:
((a 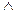 b)
b)  c)
c)  (a
(a  (b
(b 
 ))
))
л
и л
и л
4) Рассмотрев подформулу (b 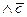 ), получим следующее распределение значений истинности: b – истинно,
), получим следующее распределение значений истинности: b – истинно,  − ложно. Получаем следующую запись:
− ложно. Получаем следующую запись:
((a 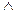 b)
b)  c)
c)  (a
(a  (b
(b 
 ))
))
л
и л
и л
и л
Таким образом, мы уже определили значения пропозиционных переменных: a – истинно, b – истинно, с – истинно (поскольку  - ложно).
- ложно).
5) Подставляя одно из полученных значений (например, с) в основание всего рассматриваемого нами высказывания, получим:
((a 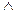 b)
b)  c)
c)  (a
(a  (b
(b 
 ))
))
л
и л
и л
и и л
6) Поскольку (a 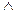 b)
b)  с является истинной импликацией, а с в ней также истинно, то ясно, что (a
с является истинной импликацией, а с в ней также истинно, то ясно, что (a 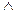 b) может принимать значения как истинности, так и ложности. Причем, значение истинности она принимает и в том случае, когда в нее подставляются полученные нами выше значения а и b как истинных:
b) может принимать значения как истинности, так и ложности. Причем, значение истинности она принимает и в том случае, когда в нее подставляются полученные нами выше значения а и b как истинных:
((a 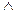 b)
b)  c)
c)  (a
(a  (b
(b 
 ))
))
л
и л
и л
и л
и
и и
Отсюда вывод, что наше предположение о ложности всей анализируемой формуле высказывания вполне может иметь место. Следовательно, данное высказывание не является однозначным (тождественно-истинным).
Следует отметить, что подробное описание процедуры анализа формулы высказывания занимает большее место, чем ее реальное осуществление. Фактически же краткая запись всей процедуры представлена в последней (результирующей) схеме. Которую можно записать и иначе:
((a  b)
b)  c)
c)  (a
(a  (b
(b 
 ))
))
и и и и и л и л и л л
3. Мы рассмотрели классификацию простых и сложных суждений и элементы основанной на таблицах истинности сложных суждений логики высказываний. Теперь перейдем к рассмотрению отношений между различными суждениями.
Как и понятия, суждения могут быть сравнимыми и несравнимыми. Нас, прежде всего, как и в случае с понятиями, интересуют сравнимые, т.е. такие, которые имеют в своем составе хотя бы один общий термин (либо S, либо P). Они, в свою очередь, делятся на два класса: совместимые, т.е. такие, которые выражают одну и ту же мысль (полностью или хотя бы частично) и несовместимые – выражающие противоположные либо противоречащие мысли об одном и том же.
Классифицируя совместимые суждения, выделяют среди них следующие группы (подклассы): равнозначащие (эквивалентные) – такие, в которых в различной форме выражается одна и та же мысль (например, «Юрий Гагарин – первый космонавт» и «Юрий Гагарин – первый человек, побывавший в космосе»); подчиненные – такие, которые имеют общий предикат, а субъект одного из суждений подчиняет субъект другого (например, «Все студенты группы успешно сдали сессию» и «Некоторые студенты группы успешно сдали сессию»).
Несовместимые суждения классифицируются на такие группы (подклассы): а) п ротивоположные (контрарные), к которым относятся общие суждения, выражающие противоположные мысли о целом классе предметов (например, «Все деревья в парке принадлежат к лиственным породам» и «Ни одно дерево в парке не принадлежит к лиственным породам»); б) противоречащие (контрадикторные), т. е. такие, которые полностью исключают друг друга, что происходит, когда одно из них что-либо утверждает обо всем классе предметов, а другое отрицает то же самое у одного либо части предметов данного класса, и наоборот (например, «Ни один из локомотивов не имеет электрическую тягу» и «Некоторые локомотивы имеют электрическую тягу»); в) подконтрарные (частично совпадающие) – такие частные суждения, которые, имея одинаковые термины (S и P), в то же время выражают противоположные мысли (например, «Некоторые дома изготовлены из железобетонных блоков» и «Некоторые дома не изготовлены из железобетонных блоков»).
Все виды отношений между сравнимыми суждениями (кроме равнозначных) можно изобразить в виде схемы, получившей в логике название «логического квадрата». На ней наглядно представлены все отношения между основными видами суждений.
A E 
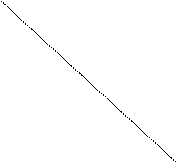

Стороны AI и EO выражают отношения подчиненности, AE – отношения противоположности, IO – отношения подконтрарности или частичного совпадения, диагонали АО и EI – отношения логического противоречия.
I О 
По углам квадрата расположены символы количественно-качественных характеристик суждений, о которых мы уже говорили в предыдущем разделе лекции (A, E, I, O).
«Логический квадрат» позволяет, благодаря своей наглядности, более четко уяснить соотношения истинности и ложности совместимых и несовместимых суждений. Дело в том, что в рассуждениях и доказательствах суждения сопоставляются не только с точки зрения их формальной непротиворечивости, но и с позиции их фактической истинности относительно друг друга.
4. Для того, чтобы определить истинность различного рода сравнимых суждений, следует пользоваться логическими правилами, которые выведены с учетом зависимости логической формы суждений от их смыслового содержания.
Правило 1. Из истинности общего подчиняющего суждения (на логическом квадрате они обозначены буквами А и Е) всегда следует истинность частного подчиненного суждения (соответственно I и О). К примеру, из истинности суждения «Bce студенты нашей группы занимаются учебно-исследовательской работой» с необходимостью следует истинность суждения «Некоторые студенты нашей группы занимаются учебно-исследовательской работой».
Правило 2. Из ложности общего подчиняющего суждения не следует ни истинность, ни ложность частного суждения, т.е. оно остается неопределенным. Например, если суждение «Все преподаватели нашего вуза являются докторами наук» – ложно, то из него не может быть однозначно выведена истинность или ложность того, что преподаватели той или иной кафедры (т.е. часть преподавателей нашего вуза) являются докторами наук.
Правило 3. Из истинности частного подчиненного суждения не следует ни истинности, ни ложности общего суждения, оно будет неопределенным. Так, из суждения «В некоторых магазинах города установлены кассовые аппараты» однозначно не следует ни истинность, ни ложность суждения «Во всех магазинах города установлены кассовые аппараты».
Правило 4. Из ложности подчиненного частного суждения с необходимостью следует ложность подчиняющего его общего суждения. Пример: ложность суждения «Некоторые металлы являются диэлектриками» определяет и ложность суждения «Все металлы диэлектрики».
Правило 5. Истинность одного из контрарных (противоположных) суждений определяет ложность другого. Иначе говоря, контрарные суждения не могут быть одновременно истинными. Так, например, если истинно суждение «Все воры – преступники», то противоположное ему суждение «Ни один вор не является преступником» обязательно ложно.
Правило 6. Ложность одного из контрарных суждений делает другое неопределенным. К примеру, ложность суждения «Все часы показывают верное время» не может определить истинность или ложность противоположного ему суждения «Ни одни часы не показывают верное время».
Правило 7. Истинность одного из подконтрарных (частично совпадающих) суждений оставляет другое неопределенным. Так, если принять за истинное суждение «Часть свидетелей дала на процессе верные показания», то невозможно определить с позиций истинности или ложности суждение «Часть свидетелей не дала на процессе верных показаний».
Правило 8. Ложность одного из подконтрарных суждений однозначно определяет истинность другого. Например, считая суждение «Некоторые кибернетические машины обладают мышлением» ложным, следует признать истинным суждение «Некоторые кибернетические машины не обладают мышлением».
Правило 9. Из двух контрадикторных, т.е. противоречащих друг другу суждений, одно будет непременно истинным, а другое обязательно ложным. Так, в случае, если суждение «Некоторые политики выступают как демагоги» является истинным, то суждение «Ни один из политиков не выступает как демагог» является обязательно ложным, и наоборот.
Все указанные выше правила определения истинности в отношениях между суждениями могут быть сведены в таблицу (см. ниже), в которой на пересечении столбцов и строк обозначается истинность (и), ложность (л) или неопределенность (н) того или иного суждения в его отношениях с другими суждениями.
| А | Е | I | О | ||
| А | и | – | л | и | л |
| А | л | – | н | н | и |
| Е | и | л | – | л | и |
| Е | л | н | – | и | н |
| I | и | н | л | – | н |
| I | л | л | и | – | и |
| О | и | л | н | н | – |
| О | л | и | л | и | – |
Лекция 4. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ЗАКОНЫ
1. Общая характеристика логических законов и их значение.
2. Закон тождества.
3. Закон непротиворечия.
4. Закон исключенного третьего.
5. Закон достаточного основания.
1. Вся жизнь убеждает человека в том, что окружающий мир наряду с его всеобщей изменчивостью отличается и относительной устойчивостью свойств и качеств многообразных предметов и процессов, их связей и отношений. Отражая этот факт, мышление человека приобрело свои специфические черты, ставшие непременными для мысли, претендующей на достоверность своих выводов. В формальной логике эти черты были сформулированы в качестве законов (принципов) правильного мышления. Речь идет об открытых Аристотелем законах тождества, непротиворечия и исключенного третьего, а также о приписываемом Г. Лейбницу законе достаточного основания.
Прежде чем рассмотреть каждый из этих законов, разберемся с самим понятием «закон». Это понятие в силу своей всеобщности и методологической значимости для науки приобрело статус философской категории. В большинстве философских систем (кроме, пожалуй, субъективно-идеалистических) закон определяется как выражение общих, необходимых, существенных, устойчивых и повторяющихся связей между явлениями. Исходя из этого, можно определить и понятие закона мышления (логического закона): логический закон есть выражение общих необходимых существенных, устойчивых и повторяющихся связей между мыслями.
Следует также подчеркнуть, что всякий закон мышления имеет объективный характер. Это значит, что люди не могут по своему усмотрению устанавливать или изменять их. Однако изучение и использование их в своей практической и теоретической деятельности вполне им по силам, делает их деятельность более результативной, помогает избегать многих ошибок и заблуждений. В то же время следует всегда помнить, что логические законы – это законы мышления, а не законы всей действительности. Эти законы функционируют в качестве принципов правильного (или, как еще говорят, логичного) мышления, обеспечивая его стройность, строгость и доказательность.
Глубокое усвоение законов правильного мышления совершенно необходимо в любой области научного познания. Без логически стройной мысли нельзя ни открыть истину, ни обосновать достоверность теоретических обобщений для практических действий. Чтобы развивать науку, нужно не только знание фактов, но и умение делать обоснованные выводы из них, обстоятельно проверять и доказывать их объективную истинность. Только при таком подходе наша мысль приобретает строгую научность, разумную убедительность и действенность.
Никакая мысль не может быть истинной, если нарушен хотя бы один из логических законов. Причем в каждой операции мышления они применяются обычно не только раздельно, но и совместно, в своем единстве. Это говорит о том, что ни один закон логики не следует игнорировать, все они имеют большое познавательное значение. Всякое несоблюдение требований этих законов нарушает внутреннюю стройность, логическую правильность наших мыслей, призванных отражать реальную действительность.
Законы правильного мышления не могут указать нам, какие именно высказывания являются в данном конкретном случае истинными, а какие − ложными. Истина всегда конкретна, т. е. вопрос об истинности всегда решается в определенных, конкретных условиях, на основе знания существа вопроса. Но без соблюдения логических законов истинного знания достичь нельзя. Они составляют неотъемлемое свойство правильного мышления. Когда мы мыслим правильно, мы всегда, даже не замечая этого, ими пользуемся. Однако бессознательное использование законов представляет собой более низкую ступень культуры мышления по сравнению с сознательным применением этих законов.
Использованные в своих пределах и на своем месте, логические законы имеют не только теоретическое, но и большое практическое значение. Они служат мощным средством обнаружения ошибок, заблуждений и разоблачения преднамеренной лжи, орудием установления истины.
Теперь, сделав эти предварительные, но необходимые замечания, можно перейти непосредственно к рассмотрению основных логических законов.
2. Закон тождества. Формулируется этот закон следующим образом: каждое понятие и суждение должны быть четко определены и оставаться однозначными (тождественными сами себе) на протяжении всего рассуждения или доказательства. На формализованном языке логики он записывается формулами:  а
а  а для суждений и А
а для суждений и А  А для понятий.
А для понятий.
В соответствии с этим законом формальная логика требует, чтобы смысловое содержание предмета нашего рассуждения не менялось произвольно в ходе логического вывода, чтобы одно понятие (или суждение) не подменялось другим. Закон тождества тем самым предостерегает от расплывчатости и неоднозначности наших мыслей.
Все, что может быть предметом нашего мышления, обладает свойством определенности. Иначе говоря, каждая вещь, всякое явление обладают определенным качеством, в котором они остаются до тех пор, пока не приобретут новое качество. А значит, до тех пор, пока это не произойдет, мы должны и понятия о них употреблять строго однозначно, т.е. в одном строго определенном смысле.
Если же предмет нашей мысли изменяется настолько, что перестает быть самим собой, тогда изменяется и понятие, которое в свою очередь также должно употребляться однозначно, в соответствии с теми признаками, которыми обладает новый предмет. Сказанное относится также и к определенному уровню познания данного предмета: новый, более глубокий уровень, конечно же, требует корректировки и углубления содержания понятия, но в пределах одной теории, выражающей определенный познавательный уровень, такое содержание изменяться не должно. Следует подчеркнуть, что закон тождества отнюдь не говорит о неизменности окружающих нас предметов и явлений. Ведь по самой своей природе законы логики правомерны только в сфере мышления.
Закон тождества не отрицает и изменчивости понятий, а значит, и суждений не только в связи с изменчивостью предметов, но и в связи с постоянным обогащением наших знаний о них. При этом нужно иметь в виду, что рассматриваемый нами закон, как и формальная логика в целом, оперирует устоявшимися понятиями. Процесс перевода одного понятия в другое не входит в ее компетенцию, а исследуется, как уже отмечалось в первой лекции, в диалектической логике.
Закон тождества выступает в качестве важнейшей нормы правильного, т.е. логичного мышления. Его нарушение ведет к серьезной логической ошибке – подмене смысла, которая может возникать как непроизвольно (что не снижает ее отрицательных последствий для доказательности каких-либо рассуждений и выводов), так и преднамеренно, в качестве одного из приемов софистики.
3. Закон непротиворечия, который является другим важнейшим законом логически правильного мышления, формулируется так: не могут быть одновременно истинными два противоположных суждения об одном и том же предмете в одном и том же отношении. Сущность этого закона, таким образом, состоит в недопустимости логического противоречия в мышлении, претендующем на истинность.
Выражая отношение логической несовместимости противоположных друг другу суждений, закон этот способствует стройности мышления, убедительности аргументации, строгости и определенности выводов, их объективной истинности.
Необходимо отметить, что в законе специально оговаривается невозможность истинности двух несовместимых суждений только в одно и то же время и в одном и том же отношении. Иначе говоря, логической противоречивости не будет, если, во-первых, речь пойдет хотя и об одном и том же предмете, но в разное время, и, во-вторых, хотя и в одно и то же время, но в разных отношениях. Рассмотрим это на простых примерах. Истинное для мая суждение о полезности дождя (в частности, для роста и созревания урожая зерновых) будет ложным в июле (когда полным ходом идет его уборка). Или же, истинное в июле суждение о вреде дождя для пшеницы (ее уборки) будет неистинным для огородных культур (помидоров, огурцов и др.), зреющих как раз именно в это время. Логической несовместимости тем более не будет, если речь в высказываниях идет о разных предметах, даже имеющих одно наименование.
Не допуская логически разноречивых мыслей, формально-логический закон непротиворечия ни в какой мере не отрицает реальных противоречий, существующих как в объективных предметах и процессах, так и в отображающем их нашем сознании (мышлении в том числе). Он лишь требует, чтобы и об этих противоречивых явлениях мы мыслили стройно, логически последовательно и аргументировано. В этом смысле закон непротиворечия, будучи законом формальной логики, по самой своей сути не может отменить диалектического закона противоречия (единства и борьбы противоположностей), раскрывающего роль противоречий как важнейших источников развития материального мира и нашего мышления о нем. В символической форме закон непротиворечия будет выглядеть таким образом:  (для понятий) и
(для понятий) и  (для суждений).
(для суждений).
Следует также подчеркнуть, что закон непротиворечия нe решает вопроса об истинности одного из противоположных суждений. Его действие ограничивается лишь тем, что одно из противоположных суждений обязательно будет ложным, что отнюдь не гарантирует истинность другого, которое может быть как истинным, так и ложным. Так, например, при истинности суждения «Все студенты группы успешно сдали зачет по логике» с необходимостью будет ложным противоположное ему суждение «Ни один из студентов группы не сдал зачет по логике». В то же время, признавая ложность второго из приведенных суждений, мы не можем однозначно утверждать истинность первого, поскольку не исключается, что некоторые студенты все же зачет по логике не сдали. Иначе говоря, этот закон не исключает одновременную ложность противоположных суждений.
4. В связи с вышесказанным о законе непротиворечия возникают вопросы: нельзя ли все же определить более точно истинность или ложность несовместимых суждений и, если это возможно, то при каком условии? Ответ на эти вопросы дает закон исключенного третьего.
Чтобы раскрыть содержание этого закона, необходимо вновь обратиться к классификации суждений, в частности, обратить внимание на различие противоположных (контрарных) и противоречащих (контрадикторных) суждений (см. в лекции «Суждение»). Если рассмотренный нами выше закон непротиворечия относится как к противоположным, так и противоречивым суждениям, то закон исключенного третьего – только к суждениям, находящимся в отношении противоречия друг к другу.
Формулировка этого закона такова: из двух противоречащих друг другу суждений одно будет обязательно истинным, другое – ложным, а третьего не дано. В символическом виде этот закон может быть представлен формулой: 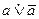 . Согласно этому закону из двух контрадикторных (противоречащих) суждений следует истинность только одного, второе же обязательно будет ложным, и не существует никакого третьего, т.е. промежуточного между ними суждения, которое было бы неопределенным, что, как мы видели, возможно в случае с противоположными (контрарными) суждениями.
. Согласно этому закону из двух контрадикторных (противоречащих) суждений следует истинность только одного, второе же обязательно будет ложным, и не существует никакого третьего, т.е. промежуточного между ними суждения, которое было бы неопределенным, что, как мы видели, возможно в случае с противоположными (контрарными) суждениями.
Нужно также подчеркнуть, что закон исключенного третьего не решает вопрос о том, какое именно из противоречащих друг другу суждений является истинным, а какое ложным. Вопрос этот решается только практикой, да и она в силу своей конкретно-исторической сущности не может решить его окончательно и бесповоротно. При этом рассматриваемый закон не отрицает и изменчивости вещей и явлений. Он лишь требует в целях определенности вывода проводить хотя бы условную грань между одним их состоянием и другим, иначе говоря, между «а» и «не-а». В этом плане нельзя абсолютизировать данный закон, как, впрочем, и другие законы формальной логики, которые имеет относительный характер, лишь условно принимая предметы и явления как устойчивые, как бы не изменяющиеся. Однако абсолютизация этой устойчивости ведет к догматизму мышления.
5. Наконец, рассмотрим еще один важнейший закон формальной логики, получивший название закона достаточного основания. Этот закон формулируется так: всякая мысль, претендующая на истинность, должна быть достаточно обоснована. Формулы для этого закона нет, поскольку он имеет прежде всего не формальный, а содержательный характер.
Закон достаточного основания требует, чтобы наши суждения о предметах, их свойствах и отношениях были не голословны, а логически вытекали из достоверных фактов, и аргументов. Суждения и выводы из них, не основанные на таких фактах и аргументах, не могут претендовать на истинность.
Рассматриваемый закон, требуя достаточной обоснованности всякого положения, не может, конечно же, указать, каким конкретным способом должно быть произведено обоснование. Каждая область знания вырабатывает свою систему форм и средств фактического и логического обоснования. Но важно для понимания закона уяснить, что все логические основания, положенные в основу аргументации того или иного положения, должны быть несомненными, фактически достоверными и, наконец, достаточными (иначе говоря, они должны быть такими, чтобы из них с необходимостью вытекала истинность данного положения).
Логический закон достаточного основания имеет свои корни в реальной действительности, в том, что все вещи и явления имеют свои предпосылки и причины. Недаром он и открыт был впервые (еще в античности) как закон объективного бытия (причинно-следственных связей), и лишь значительно позже (в ХVII веке) был сформулирован Г. Лейбницем как закон мышления. Следует подчеркнуть, что логическую обоснованность нельзя отождествлять с причинно-следственной связью в объективном мире. Они совпадают далеко не всегда. Так, логическим основанием может иногда служить простая временная последовательность событий, если она постоянно повторяется (например, «Вспыхнула молния – сейчас прогремит гром»), или следствие в его обратном отношении к причине («Термометр показывает повышение температуры, значит, на улице стало теплее»). И, тем не менее, закон достаточного основания и принцип причинности теснейшим образам взаимосвязаны. Поэтому нарушение закона достаточного основания делает наше мышление не соответствующим объективному ходу вещей, а потому неистинным, таит в себе опасность субъективного произвола и даже сознательной лжи.
Глубокое усвоение законов логического мышления совершенно необходимо в любой области интеллектуальной деятельности. Чтобы правильно мыслить, как показывает опыт, мало только знания фактов. Не менее важно умение сделать обоснованные выводы из них. Только в этом случае наша мысль приобретает строгость, логическую последовательность, убедительность и может по настоящему претендовать на истинность.
Лекция 5. УМОЗАКЛЮЧЕНИЕ
1. Умозаключение как форма мышления, его структура, типы и виды.
2. Основные типы и виды умозаключений.
3. Непосредственные и опосредованные умозаключения. Основные виды непосредственных умозаключений.
1. Наряду с понятиями и суждениями еще одной важнейшей формой мышления является умозаключение. Причем, если понятия и суждения представляют собой чаще всего выражение знаний, приобретаемых непосредственно в опыте мыслящего субъекта - человека, то умозаключение – это основная форма опосредствованного знания, получаемого в ходе логического опыта из данных опыта или же из предварительно выведенного, но прошедшего опытную проверку знания.
Поиск по сайту: