 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
РЕШЕНИЕ. Алгоритм решения задачи следующий:
Алгоритм решения задачи следующий:
1 Определить qо по формуле (4).
k = r / (q –1) (остаток от деления)
(4)
k = 10/3 = 1; q0 = 4.
2 Упорядоченный по убыванию список вероятностей p1, p2, …pr заменяют новым упорядоченным списком вида: p1, p2,.. pj, p,…pr–qo, где p = pr–qo+1+ …+ pr (т.е. суммируют последние qо штук элементов списка и создают новый упорядоченный список, в который входит полученная сумма); процесс суммирования и упорядочивания (но уже суммируют последние q штукэлементов) продолжается до тех пор, пока в списке вероятностей останется ровно q элементов.
Упорядоченный список 1 (10 чисел) 0,34; 0,18; 0,15; 0,05;… 0,05; 0,04; 0,04
Упорядоченный список 2 (7 чисел) 0,34; 0,18; 0,18; 0,15; 0,05; 0,05; 0,05
Упорядоченный список 3 (4 числа) 0,34; 0,3; 0,18; 0,18;
3 Для последнего свернутого в п.2 списка строится одноярусное кодовое дерево (из начальной вершины выходит q ребер, каждому из которых приписывается буква алфавита O, а каждой вершине 1–го яруса вероятности из последнего свернутого списка).
4 Построить 2–й, 3–й и другие ярусы кодового дерева, на которых развернуть просуммированные вероятности последнего, предпоследнего и т.д. списков(вершины, которым приписаны вероятности букв входного алфавита на любом ярусе, становятся концевыми); в результате таких действий получим кодовое дерево, в котором r концевых вершин и каждой из которых приписана вероятность pj. Выписав цепи из нулевой вершины к концевым (перечень ребер), получим схему кодирования с минимальной избыточностью.
Величина среднего превышения длины закодированного сообщения над длиной самого сообщения определим по формуле:
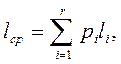= 0,34 + 0,18 + (0,3+0,18)х2 = 1,48.
Варианты заданий 1, 2 темы 6 для самостоятельной подготовки
Таблица вариантов к заданиям 1 и 2
| Вариант | r | q | p1, p2, …pr |
| 0,3; 0,22; 0,14 …. | |||
| 0,35; 0,21; 0,13 …. | |||
| 0,25; 0,24; 0,16… | |||
| 0,26; 0,22; 0,14… | |||
| 0,34; 0,18; 0,15… | |||
| 0,25; 0,22; 0,18… | |||
| 0,25; 0,24; 0,16 | |||
| 0,3; 0,22; 0,14 | |||
| 0,26; 0,22; 0,14 | |||
| 0,34; 0,18; 0,15… |
Примечание Список вероятностей дополнить самостоятельно до общей суммы 1.
Вопросы по теории темы 6 для самостоятельной подготовки
1 Алгоритм построение кодов с минимальной избыточностью (кодов Хаффмана) при равновероятностном появлении букв входного алфавита.
2 Алгоритм построение кодов с минимальной избыточностью (кодов Хаффмана) при заданных вероятностях появлении букв входного алфавита.
3 Самокорректирующиеся коды (коды Хемминга). Принципы их построения
Тема 7
Поиск по сайту: