АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вычислительная процедура

Читайте также:
  1. Адміністративна процедура при надання адміністративних послуг.
  2. Алгоритм проверки значимости регрессоров во множественной регрессионной модели: выдвигаемая статистическая гипотеза, процедура ее проверки, формулы для расчета статистики.
  3. Биржевые товары: отличительные черты, виды и требования к качеству. Процедура допуска биржевого товара к торгам.
  4. Вопрос Санація, мирова угода та ліквідаційна процедура при визнанні боржника банкрутом.
  5. Глава 10: Процедура оценивания 349
  6. Как называется статистическая процедура, построенная в теореме Гаусса-Маркова? метод наименьших квадратов
  7. Крок 10. Експертна процедура
  8. Ліквідаційна процедура
  9. Мировое соглашение в процедурах банкротства
  10. Особенности заключения мирового соглашения в различных процедурах банкротства и его результат
  11. Понятие инструментальной переменной. Процедура получения состоятельных оценок параметров модели при нарушении четвертой предпосылки теоремы Гаусса-Маркова.

Общие сведения о численных методах оптимизации

Определение 1. Численный метод - это правило (алгоритм), в соответствии с которым вычисляется последовательность вели­чин , которая должна сходиться к реше­нию оптимизационной задачи .

 

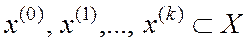- приближения к решению

 

Правило формирования последовательности

 

(1)

 

Вектор задает направление движения в пространстве ,

 

число - величину "шага" при переходе из точки в точку .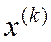

 

 

 

Если используется информация только о целевой функции , алгоритм называют алгоритмом нулевого порядка; если используется информация о производных первого порядка - алгоритмом первого порядка; если используются вторые производные - алгоритмом второго порядка и т.д.

 

Если алгоритм за конечное число шагов приводит в точку , его называют конечношаговым, иначе - бесконечношаговым.

 

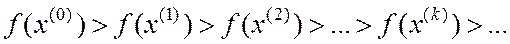(2)

 

Алгоритм (1) относят к методам спуска

 

1. Выбор направление поиска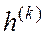

 

Оп ределение 1. Будем говорить, что вектор 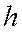в точке 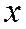задает направление убывания функции (в задаче минимизации), если при всех достаточно ма­лых величинах выполняется условие . Такой вектор называют направлением убывания

 

2. Правило выбора параметра

 

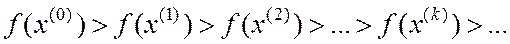
а) ,

 

б) ,

 

 

в) (3)

 

3. Скорость сходимости алгоритма:

 

· линейная скорость, скорость геометрической прогрессии

· сверхлинейная скорость

· квадратичная скорость

 

4. Правилами останова алгоритма

 

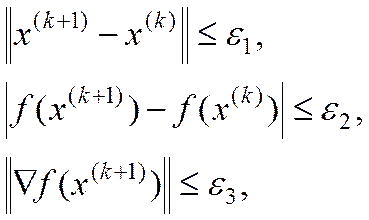(4)

 

где 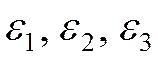- некоторые достаточно малые положительные числа.

 

4. Выбор точки начального приближения

 

2.5. Алгоритмы многомерной оптимизации

 

 

(5)

 

Градиентные методы поиска

Методы используют информацию о градиенте це­левой функции и относятся к методам первого порядка.

(6)

дифференцируема на

. (7)

- (8)

 

(9)

1. Простейший градиентный метод ;

2. Метод наискорейшего спуска

(10)

3. Градиентный метод с дроблением шага

3.1. часто ;

 

3.2. к следующей итерации

 

 

 

Вычислительная процедура

 

1. ,

 

2. ,

 

3. ,

 

4.

 

5. Проверка условий останова: если выполняются ;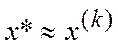

иначе к п. 2

 

Особенности методов:

· относятся к локальным методам оптимизации;

· используются для решения как одномерных, так и многомерных экстремальных задач;

· выпуклая ЦФ – метод сходится к точке минимума;

сильно выпуклая ЦФ - метод сходится к точке минимума с линейной скоростью;

невыпуклая ЦФ - метод сходится ко множеству стационарных точек

· градиентные методы относятся к методам спуска ;

· низкая скорость сходимости в окрестности точки минимума; метод чувствителен к ошибкам вычислений; градиентные методы целесообразно применять на начальном этапе оптимизационной процедуры.

Метод Ньютона

(11)

- оптимизационный метод Ньютона

 

Особенности метода Ньютона

 

1. Трудоемкость, обусловленная вычислением и обращением матрицы Гессе на каждой итерации;

2. Выбор ;

3. Метод Ньютона сходится к точке минимума произвольной ЦФ с квадратичной скоростью, если матрица Гессе положительно определена, а располагается «достаточно близко» к .

 

Метод Ньютона с регулировкой шага:

 

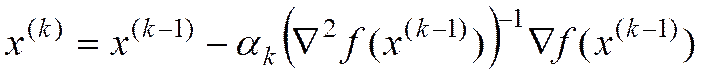(12)

 

,

Скорость сходимости – сверхлинейная;

квадратичная


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)