Ряды распределения

Основные группы статистических характеристик.

1.Показатели центра распределения.

2.Показатели вариации.

3.Показатели асимметрии и эксцесса.

4.Нормальное распределение: понятие, признаки и особенности.

1. Получив в свое распоряжение статистические данные, характеризующие какое-либо массовое явление, исследователь экономист должен прежде всего подумать о систематизации этих данных, о проведении их в какой-то порядок.

Недостаточно их расположить в порядке возрастания или убывания величины показаний. Исследователь не сможет ничего сказать о том, какие закономерности заложены в распределении данных. Около какой величины группируется большинство показаний, какие имеются отклонения от этой величины в ту или иную сторону, какова общая картина распределения?

На эти и на другие вопросы исследователь может ответить, продолжив работу с рядами распределения и рассчитав основные показатели, характеризующие данные ряды распределения.

Для большинства статистических распределений характерным является концентрация значений признаков «х» около некоторого центра распределения.

Центр распределения характеризуется следующими показателями:

1.средняя арифметическая.

2.мода.

3.медиана.

Средней величиной признака «х» некоторой статистической совокупности называется то уравненное значение признака, которое можно придать всем элементам совокупности, сохраняя неизменным ее определяющее свойство по данному признаку.

Основным и наиболее распространенным видом является средняя арифметическая. В зависимости от содержания исходных данных она может выражаться в 2 формах:

1.средняя арифметическая простая

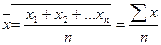
2.средняя арифметическая взвешенная

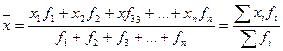
Что касается самой техники вычисления средней арифметической взвешенной в интервальном ряду, то она не сложна. Прежде чем приступить к этой операции, необходимо заменить интервалы их средними значениями. Эти средние значения интервалов определяются как полусуммы крайних их значений.

Какая из двух форм средней арифметической является более точной?

Конечно, средняя арифметическая простая, поскольку в расчетах используются все значения признака. А при расчете средней арифметической взвешенной используется усредненное значение признака в каждом отдельно взятом интервале.

Формула средней арифметической взвешенной применяется в тех случаях, когда признак сгруппирован.

Для характеристики структуры совокупности применяются особые показатели, которые можно назвать структурными средними. К таким показателям относятся мода и медиана.

Мода(Мо)- это варианта, которая встречается в совокупности наибольшее число раз.

В дискретном ряду распределения мода определяется визуально, т.е. это варианта, которой соответствует наибольшее число частоты. Например, по приведенным данным наибольшим спросом обуви пользуется размер 37.

Размер обуви Число купленных пар

34 2

35 9

36 18 Мо=37

37 24

38 20

39 11

40 2

Самый грубый прием определения моды в интервальном вариационном ряду заключается в простом указании середины того интервала, который соответствует наибольшей частоте.

Более точно моду можно определить, лишь сопоставляя частоты трех последовательных интервалов, в среднем из которых лежит мода. Конкретное значение моды для интервального ряда распределения определяется формулой:

Мо=х₀+і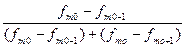

Где: х₀-нижняя граница модального интервала;

І- величина (шаг интервала);

F_mo- частота модального интервала;

F_mo-1- частота предмодального интервала;

F_mo+1- частота послемодального интервала.

Пример. Изучение роста студентов.

Х f

155-160 5

160-165 8

165-170 12

170-175 21

175-180 10

180-185 3

185-190 1 Мо=170+5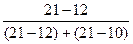

Моду можно определить графически в интервальном ряду распределения.

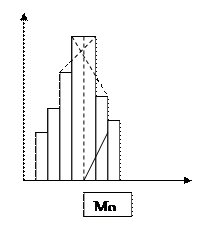
В одной и той же совокупности мода может принимать несколько значений. Наличие двух и большего числа мод является признаком неоднородности данных.

Если в дискретном ряду ни один из вариантов признака не повторяется или встречается только один раз, мода отсутствует.

В интервальном ряду с равными частотами значение моды также невозможно установить.

Следовательно, мода- это единственный вид средней, который в произвольно взятой совокупности может отсутствовать, либо иметь более одного значения.

Мода широко используется в коммерческой практике при изучении покупательского спроса(при определении размеров одежды и обуви, которые пользуются более широким спросом), регистрации цен на рынках. Один раз в месяц 21 числа на всех официальных рынках происходит регистрация цен.

Мода на практике применяется в том случае, когда средняя арифметическая не имеет смысла. Медиана (Ме)- это варианта, которая строго делит ряд распределения пополам. Она делит совокупность на две равные по численности части. В первую половину входят элементы со значениями признака х ≤ Ме, во вторую х ≥ Ме.

Медиана-это такое значение признака, которым обладает центральный член ранжированного ряда, т.е. составленного в порядке возрастания или убывания значений признака.

В дискретном ряду распределения медиана находится следующим образом:

-двигаясь вниз по ряду накопленных частот находят такое его значение, которое равно половине всех частот или первым содержит эту половину. Такой частоте соответствует варианта равная медиане.

Пример. Количество детей в обследованных семьях:

х f f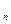

0 1 1

1 10 11

2 25 36 Мо=2

3 8 44

4 4 48

5 2 50

В интервальном ряду распределения медиана определяется по формуле:

Ме=х₀+i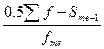

Где: х₀-нижняя граница модального интервала;

І- величина (шаг интервала);

S_me-1 – сумма накопленных частот предмедианного интервала;

∑F- сумма частот;

F_me- частота медианного интервала.

Пример. Изучение роста студентов.

х f f

155-160 5 5

160-165 8 13

165-170 12 25

170-175 21 46 Ме=170+5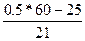

175-180 10 56

180-185 3 59

185-190 1 60

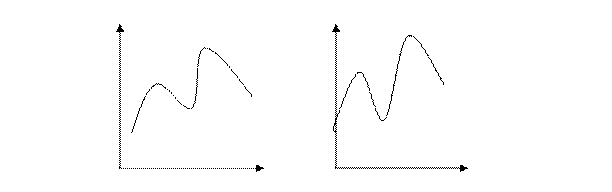
Медиану, так же как и моду, можно определить графически. Для этого используются кумулятивные кривые, построенные по накопленным частотам.

По оси х откладывается значение варианты(если речь идет о дискретном ряде) или значение середины интервала(если интервальный ряд), а на оси у- накопленные частоты.

Накопленной частоте, равной половине всех частот или первой содержащей эту половину, на оси х соответствует значение, равное медиане.

Интервальный ряд. Дискретный ряд.

Несмотря на то, что средняя, мода и медиана по-разному определяются и отвечают на разные вопросы, но это не значит, что они не зависимы друг от друга и могут резко отличаться по величине в качественно однородной совокупности.

Медиана находит практическое применение вследствие особого свойства- сумма абсолютных отклонений членов ряда от Ме есть величина наименьшая.∑(х-Ме)=мин.

Вышеназванное свойство медианы находит широкое применение в маркетинговой деятельности.

Расположение магазинов (х- 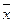) (х-Ме)

от базы снабжения, км (х)

1 2 3 2

2 3 2 1

3 4 1 0

4 6 1 2

5 16 5 6

Итого 25 13 11

Маркетинг- это комплексная система управления рынком товаров, регулирования и изучения рыночных процессов, соотношения предложения и спроса. Главная цель маркетинга- обеспечить управляемость процессами сбыта, продажи товаров, ценообразования и т.д., поиск наиболее эффективных путей движения товаров.

В симметричных распределениях рассмотренные выше средние равны:

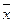=Мо=Ме

В умеренно-ассиметричных распределениях соблюдается равенство:

Ме=1/2Мо+2/3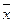

Из этого следует, что сочетание моды, медианы и средней важно и для характеристики типа распределения.

2. Показатели вариации.

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака.

Она возникает в результате того, что на индивидуальные значения признака действуют разнообразные факторы, которые по-разному сочетаются в каждом отдельном случае.

Средняя величина, как уже отмечалось выше, - это абстрактная, обобщающая характеристика признака изучаемой совокупности.

Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней:

- в одних случаях варианты тесно концентрируются около некоторых центральных значений признака х. В таких случаях средняя хорошо представляет всю совокупность.

- в других- наблюдается значительная разбросанность вариант относительно центра, и средняя плохо представляет всю совокупность.

Так, например, в двух сравниваемых районах урожайность какой-либо культуры в среднем для всех хозяйств может быть одинаковой, но в одном из этих районов имеются передовые хозяйства с высокой урожайностью, а в другом- почти все колхозы группируются по размеру урожайности около средней величины.

Таким образом, показатели центра (средняя, мода и медиана) не дают полной информации о форме распределения, поэтому возникает необходимость изучения степени рассеивания признака относительно центра.

Колеблемость отдельных значений характеризуют показатели вариации. Наиболее распространенными из них являются: дисперсия, среднее квадратическое отклонение, размах вариации, среднее линейное отклонение. Это абсолютные показатели вариации.

1.Абсолютный размах вариации- определяется как разность между наибольшим и наименьшим значениями вариант.

Ra=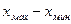

Например, различие между максимальной и минимальной пенсией различных групп населения, заработной платой различных категорий работающих или нормами выработки у рабочих определенной специальности или квалификации; размах вариации урожайности в хозяйствах фермеров района, области.

Например, размах вариации применяется при контроле качества продукции для определения влияния систематически действующих причин на производственный процесс. Для этого отбирают через определенные промежутки времени несколько деталей и производят их измерение. Рассчитав по данным этих выборок показатели размаха вариации, на основе сопоставления результатов вычислений судят об устойчивости производственного процесса.

Достоинства:

1.Имеет единицы измерения.

2.Простота исчисления и истолкования.

Недостатки:

1.Не отражает отклонений всех вариант в ряду распределения.

2.Базируется на крайних значениях уровней.

2.Среднее линейное отклонение- определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:

= - простая форма

= -взвешенная форма

где:х -индивидуальное значение признака

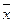-их средняя величина

n-численность единиц совокупности

f- вес.

Достоинства:

1.Имеет единицы измерения.

2.Показывает вариацию признака внутри совокупности.

Недостатки:

1.не учитывает знак отклонений.

3.средний квадрат отклонений(дисперсия)- определяется как средняя из отклонений, возведенных в квадрат:

-простая форма

- взвешенная форма

Достоинства:

1.Учитывает знак отклонений.

2.Учитывает вариацию внутри совокупности.

Недостатки:

1.Величина абстрактная, не имеет единиц измерения.

2.Дает искаженное представление о величине отклонений, измеряя их в квадратных единицах.

4.Среднее квадратическое отклонение- представляет собой корень квадратный из дисперсии:

√ - простая форма

√ - взвешенная форма

Достоинства:

1.имеет единицы измерения.

2.предопределяет форму рассеивания.

3.Дает наиболее точное представление о величине отклонеий.

Среднее квадратическое отклонеие является мерилом надежности средней: чем меньше среднее квадратическое отклонеие, тем лучше средняя арифметическая отражает собой всю представленную совокупность.

Для характеристики меры колеблемости изучаемого признака исчисляются относительные показатели вариации. Они позволяют сравнивать характер рассеивания в различных распределениях(различные единицы измерения, наблюдения одного и того же признака в двух совокупностях, при различных значениях средней, при сравнении разноименных совокупностей).

Например. Если среднее отклонение урожайности пшеницы( или ) по хозяйствам района составляет 5 ц/га, а кукурузы на зерно-15 ц/га. То непосредственное сопоставление этих данных недостаточно для сравнительной характеристики вариации этих двух культур, уровень урожайности которых разный.

Если речь идет о сравнении признаков, имеющих различные единицы измерения, то примером может быть определение темпов роста заработной платы и производительности труда. Заработная плата выражается в денежных единицах измерения, а производительность труда имеет и стоимостное выражение и может выражаться в натуральных единицах измерения.

Расчет относительных показателей осуществляется как отношение абсолютного показателя к средней арифметической, умноженной на 100 %.

1.Относительный размах вариации(коэффициент осцилляции):

Ro=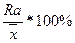

2.Коэффициент вариации линейный:

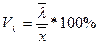
3.Коэффициент вариации квадратический:

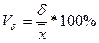
Коэффициент вариации квадратический, также как и среднее квадратическое отклонение, нашел самое широкое применение в статистике.

3. Показатели асимметрии и эксцесса.

К числу характеристик ряда распределения относятся и показатели, характеризующие его «скошенность»- асимметричность, а также его «крутость»- островершинность и плосковершинность.

Если численность групп убывает в одну сторону кривой быстрее, чем в другую, то исследователь имеет дело с асимметрией распределения.

Если более длинная ветвь кривой приходится на большие значения признака, лежащие на правой стороне графика, то такая асимметрия называется правосторонней или положительной. В противном случае асимметрия считается левосторонней или отрицательной.

Кривые распределения, относящиеся к социально-экономическим явлениям,очень часто обнаруживают асимметрию, особенно правостороннюю.

Правосторонней асимметрией характеризуется распределение промышленных предприятий по числу рабочих или распределение магазинов по величине оборота, так как численность более мелких предприятий или магазинов всегда больше, чем численность крупных.

Асимметричность, или скошенность распределения, может быть измерена.

Для измерения асимметрии распределения в математической статистике предлагаются два варианта:

Ка= - коэффициент асимметрии

А = - степень асимметрии

где: М₃- центральный момент третьего порядка

М₃₌

- среднее квадратическое отклонения, возведенное в третью степень

А - степень асимметрии. Наиболее точный и распространенный показатель.

Для теоретических кривых нормального распределения А =0

При правосторонней(положительной)асимметрии А >0.

При левосторонней (отрицательной) асимметрии А <0.

Эксцесс- это отклонение кривых от кривой нормального распределения по вертикали.

Степень эксцесса можно измерить с помощью показателя:

Е_х=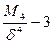

Где: М₄- центральный момент четвертого порядка

М₄ =

- среднее квадратическое отклонение, возведенное в 4 степень.

Для теоретических кривых нормального распределения Е_х=0.

При островершинном распределении или положительном эксцессе Е_х >0.

При плосковершинном распределении или отрицательном эксцессе Е_х <0.

4. Нормальное распределение.

Распределение частот в произвольно взятой совокупности имеет свои особенности, отличающие его от множества других. В то же время все разнообразие эмпирических распределений может быть подразделено на классы в соответствии с некоторыми общими свойствами.

Большинство выборочных данных относится к одному из четырех классов частотного распределения.

1.прямоугольное(равномерное).

2.бимодальное.

3.экспоненциальное.

4.колоколобразное.

1.прямоугольное или равномерное распределение. Все значения признака имеют одинаковую частоту. Распределению этого класса подчинено появление шаров из барабана в тиражах спортивной лотереи. Каждый номер может появиться только один раз. Графически это выглядит следующим образом:

2.бимодальное распределение характерно для неоднородных данных. Оно может быть результатом наложения двух нормальных распределений. Наличие бимодальности является основанием для поиска источников неоднородности изучаемой совокупности.

3.Среди экспоненциальных распределений преобладают убывающие. Они особенно распространены в экономике. Так, среди различных уровней дохода, получаемого гражданами любого государства, низкие значения встречаются чаще. Частоты, соответствующие более высоким доходам, устойчиво убывают.

4.Четвертый класс- наиболее распространенная форма распределения.

Он встречается настолько часто, что одна из его разновидностей называется нормальным распределением. Нормально распределены различные показатели умственного и физического развития людей(коэффициент умственных способностей, рост, вес и др.). В странах с устойчивой рыночной экономикой нормально распределяются дневные изменения курса ценных бумаг. К нормальному распределению относится распределение коров по дневному удою. Встречи экономиста с нормальным распределением более редки, чем представителей биологических или технических наук. Это обстоятельство обусловлено природой социально-экономических явлений, отличающихся большой сложностью.

Существует несколько разновидностей колоколообразного распределения:

-нормальное распределение

-распределение Стьюдента

-распределение Пуассона.

Но наиболее широкое распространение получило нормальное распределение.

История открытия нормального распределения связана с именами Гаусса(1809) и Лапласа(1812). Поэтому его чаще называют законом Гаусса, вторым законом Лапласа, распределением Гаусса-Лапласа.

Термин «нормальное распределение» введен Пирсоном.

Таким образом, нормальное распределение играет роль стандарта, с которым сравнивают изучаемую совокупность.

Нормальное распределение признака наблюдается в тех случаях, когда на величину признака явления действует множество случайных независимых или слабозависимых факторов, каждый из которых играет в общем числе незначительную роль (отсутствуют доминирующие факторы).

Нормальным распределением в математической статистике называется распределение, которое может быть выражено следующим уравнением:

У=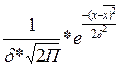

Где:у-ордината кривой распределения

х-заданное значение признака

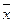- средняя арифметическая

-среднее квадратическое отклонение

П-величина, выражающая отношение длины окружности к длине ее диаметра.

Е-основание натуральных логарифмов.

Если принять t, то уравнение имеет вид

у=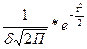

Кривая нормального распределения – это колокообразная кривая, ветви которой располагаются симметрично относительно к оси х.

Гальтоном был сконструирован прибор, который представляет собой хорошо отколированную гладкую доску, окаймленную невысоким бортиком. В ней вколоты перпендикулярно несколько рядов булавок в шахматном порядке. В верхней части доски сделано отверствие как раз против вертикальной линии, делящей доску пополам. Доска становится наклонно, и экспериментатор ссыпает в отверствие дробь. Дробинки катятся по доске, ударяясь о булавки.

Двигаясь вниз дробинки испытывают на себе совместное действие многочисленных друг от друга не зависимых и противоположно направленных воздействий. Дробинки, скопившиеся в итоге испытания в нижней части прибора, наглядно представляют нормальное распределение.

Вообще же не существует какой-либо одной нормальной кривой и не совсем уместно ссылаться на эту в обычном смысле «нормальную кривую» как на какую-то конкретную кривую.

Кривая распределения, выражающая общую закономерность данного типа распределения, называется теоретической кривой распределения. Для построения кривой нормального распределения необходимы два параметра- средняя арифметическая и среднее квадратическое отклонение.

Вспомним правило трех сигм: по нормальному распределению колеблемость индивидуальных значений признака находится в пределах . По данному закону в пределах находится 68.3 % всех изучаемых единиц совокупности; в пределах находится 95.4 % всех изучаемых единиц совокупности; в пределах находится 99.7 % всех изучаемых единиц совокупности.

Например, из 60 опрошенных студентов по их росту, как минимум 40 человек(60*68.3%) будут иметь рост , как минимум 57 человек(60*95.4%) будут иметь рост и как минимум 59 человек(60*99.7%) будут иметь рост .

Фактическое распределение отличается от теоретического в силу влияния случайных факторов. Их влияние сглаживается с увеличением объема исследуемой совокупности. В силу этого большое значение имеет сопоставление фактических кривых распределения с теоретическими.

Признаки нормального распределения.

1.Особая схема расположения частот в рядах распределения; вначале их значения нарастают- затем убывают.

2.Полигон. построенный на базе гистограммы имеет одну вершину и ветви его располагаются примерно симметрично относительно этой вершины.

3.Показатели центра совпадают или близки друг к другу:

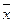=Мо=Ме

4.Выполняется правило трех сигм.

5.Показатели асимметрии и эксцесса равны 0:

Ка=А =Е_х =0

6.Между эмперическими и теоретическими частотами распределения расхождения носят случайный характер.

В разделе оценка статистических гипотез математическая статистика рассматривает вопросы о критериях согласия, при помощи которых проверяется гипотеза о соответствии или несоответствии того или иного теоретического закона распределения, принятого для отражения некоторого эмперического расперделения.

Критерии согласия должны дать ответ на вопрос: можно ли принять для данного эмперического распределения модель, выражаемую некоторым теоретическим законом распределения.

В целом процедура проверки гипотезы о соответствии эмперического распределения теоретическому- нормальному распределению складывается из следующих этапов:

1.нахождение оценок параметров имеющегося распределения на основе выборки.

2.вычисление теоретических частот на основе полученных параметров и исходя из теоретической функции частот.

3.оценка близости эмперического распределения теоретическому на основе критерия «хи-квадрат».

Придерживаясь предложенного порядка, рассмотрим эти этапы более подробно.

Первый этап-нахождение оценок параметров- это расчет показателей, которые мы с вами рассматривали заранее(показатели центра, показатели вариации и т.д.)

Для сравнения фактического распределения с теоретической кривой нормального распределения, необходимо рассчитать теоретические частоты, т.е. те частоты, которые должна иметь кривая нормального распределения данного изучаемого явления. Теоретические частоты можно определить по аналитическому уравнению кривой нормального распределения:

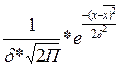У= у=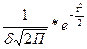

Полученные теоретические частоты (f ) наносят на график эмпирического распределения и делают попытку графически оценить близость полигона и кривой нормального распределения. Однако, такое сравнение носит субьективный характер.

Как же теперь ответить на вопрос: случайно ли такое расхождение фактического уровня с теоретической кривой или оно обусловлено причинами, носящими уже не случайный характер?

Исследователь выдвигает здесь гипотезу о случайном расхождении между фактическими частотами и частотами теоретическими, и если она подтверждается, то будет соблюдаться 6 признаков нормального распределения.

Однозначно близость эмпирического и теоретического распределения можно оценить, используя критерии согласия. Таких критериев математическая статистика предлагает несколько. Но наиболее употребляемым является критерий, предложенный К.Пирсоном и известный под названием критерия «хи-квадрат».

Для применения этого критерия ставятся следующие условия:

-общая численность частот распределения должна быть достаточно большой, не менее 50;

-число единиц в интервале не должно быть слишком малым (не менее 5).

Если в распределении имеются группы с небольшим числом частот, а чаще всего это крайние интервалы(первый и последний), то группы сливаются посредством слияния интервалом таким образом, чтобы вновь полученные имели численность единиц в каждой более 5.

Вычисление самого критерия «хи-квадрат» производится по формуле:

Х²=∑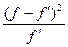

Где: f- частоты фактического распределения;

-частоты теоретические.

После вычисления критерия «хи-квадрат» необходимо полученное значение сравнить с табличным.

Таблица значений существенности «хи-квадрата» составлена с учетом числа степеней свободы и уровнем значимости.

Так как теоретическая нормальная кривая исчисляется при условии, что сумма ее частот должна быть равна численности фактического распеределения, а ее среднее арифметическое и средняя квадратическое отклонение равны фактическим, то число степеней свободы для оценки существенности «хи-квадрата» определяется как где: n-число интервалов в данном распределении, b-число параметров теоретического распределения(в=2, х=6).

Если фактическое значение «хи-квадрата» меньше табличного, т.е. х²_факт<х²_табл.,то можно сделать вывод, что расхождения между фактическими и теоретическими частотами носят случайный характер, а следовательно, подтверждается гипотеза о том, что анализируемое распределение подчиняется закону нормального распределения.

Поиск по сайту: