 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теоретические упражнения
VIII. ВЕКТОРНЫЙ АНАЛИЗ
Теоретические вопросы
1. Скалярное поле. Производная по направлению.
2. Градиент, его свойства. Инвариантное определение градиента.
3. Векторное поле. Поток векторного поля через поверхность, его физический смысл.
4. Формула Остроградского.
5. Дивергенция векторного поля, ее физический смысл. Инвариантное определение дивергенции. Свойства дивергенции.
6. Соленоидальное поле, его основные свойства.
7. Линейный интеграл в векторном поле, его свойства и физический смысл.
8. Циркуляция векторного поля, ее гидродинамический смысл.
9. Формула Стокса.
10. Ротор векторного поля, его свойства. Инвариантное определение ротора.
11. Условия независимости линейного интеграла от формы пути интегрирования.
12. Потенциальное поле. Условия потенциальности.
Теоретические упражнения
1. Найти производную скалярного поля 
по направлению градиента скалярного поля 
.
2. Найти градиент скалярного поля 
, где 
— постоянный вектор, а 
— радиус-вектор. Каковы поверхности уровня этого поля и как они расположены по отношению к вектору ?
3. Доказать, что если 
— замкнутая кусочно-гладкая поверхность и — ненулевой постоянный вектор, то
где 
— вектор, нормальный к поверхности .
4. Доказать формулу
где 
; — поверхность, ограничивающая объем 
; 
— орт внешней нормали к поверхности . Установить условия применимости формулы.
5. Доказать, что если функция 
удовлетворяет уравнению Лапласа
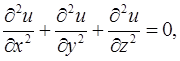то 
где 
— производная по направлению нормали к кусочно-гладкой замкнутой поверхности .
6. Доказать, что если функция является многочленом второй степени и — кусочно-гладкая замкнутая поверхность, то интеграл
пропорционален объему, ограниченному поверхностью .
7. Пусть 
, где 
— линейные функции от 
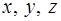и пусть 
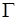— замкнутая кусочно-гладкая кривая, расположенная в некоторой плоскости Доказать, что если циркуляция 
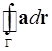отлична от нуля, то она пропорциональна площади
фигуры, ограниченной контуром .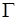
8. Твердое тело вращается с постоянной угловой скоростью вокруг неподвижной оси, проходящей через начало координат. Вектор угловой скорости 
. Определить ротор и дивергенцию поля линейных скоростей 
точек тела (здесь — радиус-вектор).
Поиск по сайту: