Емпіричні оцінки

Звіт

про проходження переддипломної практики

у ВНЗ «УжНУ»

з 9.02.2015 по 20.02.2015

студентки-практикантки 6-го курсу

математичного факультету

Рішко Марини Іванівни

Я, Рішко Марина Іванівна, проходила практику в Моци Андрія Івановича.

Перший тиждень практики-огляд літератури і підготовка до державного екзамену.

Другий тиждень- підготовка до державного екзамену,опрацювання теоретичної частини дипломної роботи по заданій темі;порівняння статистичних методів дослідження оцінок невідомих параметрів;оцінювання параметрів розподілу:незміщені оцінки,конзистентні оцінки; методи одержання оцінок: метод моментів,метод максимальної правдоподібності; підготовка звіту про проходження практики.

Під час даної практики я здобула корисні навички,які надіюсь в майбутньому зможу використати в своїй професійній діяльності.

20.02.2015 /Рішко М.І.

Статистичні оцінки

Означення: Статистика,яка приймається за наближене значення невідомого параметру,називається статистичною оцінкою.

Емпіричні оцінки

Означення: Нехай -вибірка з неперервного розподілу F. Функцію (), визначену на рівністю

( ) =

будемо називати емпіричною функцією розподілу.

Для кожного фіксованого емпірична функція розподілу () є незміщеною та конзистентною оцінкою F().

Означення: Послідовність 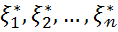будемо називати варіаційним рядом послідовності ,а 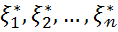- порядковими статистиками.

Означення: Оцінку параметра 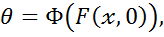одержану за формулою = 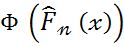будемо називати емпіричним вибірковим значенням параметра

Зокрема,

- емпіричне (вибіркове) середнє,

-емпірична (вибіркова) дисперсія.

Теорема: Нехай - вибірка з розподілу F і 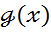- борелівська функція на зі значенням в ,якщо

То вибіркове значення величини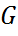

є консистентною й незміщеною оцінкою параметра .

Література

1.Теорія ймовірностей та математична статистика.

П.В. Слюсарчук, Ужгород 2005р.

2. Математична статистика в прикладах і задачах.

В.М. Турчин, Дніпропетровськ 1998р.

20.02.2015 Рішко.М.І.

Поиск по сайту: