 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ПОСТОЯННОГО ТОКА
ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ ЦЕПЕЙ
по дисциплине «Электротехника и электроника»
Вариант №84
В.И. Субханкулов
Выполнили: ст. гр. БМС-13-01 ____________
(подпись, дата)
____________ К.С. Сидоров
(подпись, дата)
Проверил: ассистент ____________ Р.Т. Хазиева
(подпись, дата)
УФА 2015
Цель работы: экспериментальное обоснование метода преобразования цепи с помощью эквивалентного генератора.
Экспериментальное обоснование метода преобразования цепи с помощью эквивалентного генератора

Рисунок 1, а – Схема для определения ЭДС эквивалентного генератора
ЭДС эквивалентного генератора Ee = U3ХХ = 227.1 В.

Рисунок 1, б – Схема для определения тока при коротком замыкании
Ток при коротком замыкании I3КЗ = 3.392А.
Внутреннее сопротивление эквивалентного источника ЭДС
Rbe = Ee / I3КЗ = 227.1 / 3.392 = 66.95 Ом.
Таблица 1 – Результат экспериментов и расчета
| Эксперимент | Расчет | ||
| U3ХХ, В | I3КЗ, А | Ee, В | Rbe, Ом |
| 227.1 | 3.392 | 227,1 | 66,46 |
Rbe = R1 ∙ R2 / (R1 + R2) = 104*188/ (104 + 188) = 66,46 Ом.

Рисунок 1, в – Схема эквивалентного генератора с нагрузкой
(режим холостого хода)

Рисунок 1, г – Схема эквивалентного генератора с нагрузкой
(режим короткого замыкания)

Рисунок 1, д – Схема эквивалентного генератора с нагрузкой
(при значении R3 = 500 Ом)
Выводы
Электрическая цепь – совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение.
Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника, установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома. Определяющее уравнение для электрического сопротивления R= U / I.
Закон Ома является основным законом электротехники, без которого нельзя обойтись при расчете электрических цепей.
Законы Кирхгофа – два основных закона электрических цепей. Первый закон устанавливает связь между суммой токов, направленных к узлу соединения (положительные), и суммой токов, направленных от узла (отрицательные).
Алгебраическая сумма сил токов In, сходящихся в любой точке разветвления проводников (узле), равна нулю, т.е. ∑(In)= 0. Например, для узла можно записать: I1 + I2 = I3 + I4 или I1 + I2 – I3 – I4 = 0.
Второй закон устанавливает связь между суммой электродвижущих сил и суммой падений напряжений на сопротивлениях замкнутого контура электрической цепи. Токи, совпадающие с произвольно выбранным направлением обхода контура, считаются положительными, а не совпадающие – отрицательными.
Алгебраическая сумма мгновенных значений ЭДС всех источников напряжения в любом контуре электрической цепи равна алгебраической сумме мгновенных значений падений напряжений на всех сопротивлениях того же контура ∑(En)=∑(InRn). Переставив ∑(InRn) в левую часть уравнения, получим ∑(En) – ∑(InRn) = 0. Алгебраическая сумма мгновенных значений напряжений на всех элементах замкнутого контура электрической цепи равна нулю.
Электрическую цепь образуют источники электрической энергии, ее приемники (потребители) и соединительные провода. В электрическую цепь обычно включают также вспомогательное оборудование: аппараты, служащие для включения и выключения электрических установок (рубильники, переключатели и др.), электроизмерительные приборы 2 (амперметры, вольтметры, ваттметры), защитные устройства (предохранители, автоматические выключатели).
В качестве источников электрической энергии применяют главным образом, электрические генераторы и гальванические элементы или аккумуляторы. Источники электрической энергии часто называют источниками питания. В приемниках электрическая энергия преобразуется в другие виды энергии. К приемникам относятся электродвигатели, различные электронагревательные приборы, лампы накаливания, электролитические ванны и др.
При расчете в схеме электрической цепи выделяют несколько основных элементов. Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов. Узел электрической цепи (схемы) – место соединения трех и более ветвей. Контур – любой замкнутый путь, проходящий по нескольким ветвям.
Расчет электрической цепи методом непосредственного применения законов Кирхгофа
Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:

Согласно второму закону Кирхгофа алгебраическая сумма напряжений на
резистивных элементах замкнутого контура равна алгебраической сумме ЭДС,входящих в этот контур.
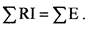
Расчет многоконтурной линейной электрической цепи, имеющей "b" ветвей с активными и пассивными элементами и "у" узлов, сводится к определению токов отдельных ветвей и напряжений на зажимах элементов, входящих в данную цепь.
Пассивной называется ветвь, не содержащая источника ЭДС. Ветвь, содержащая источник ЭДС, называется активной.
1-й закон Кирхгофа применяют к независимым узлам, т.е. таким, которые
отличаются друг от друга хотя бы одной новой ветвью, что позволяет получить (y - I) уравнений.
Недостающие уравнения в количестве b - (у - I) составляют, исходя из
второго закона Кирхгофа. Уравнение записывают для независимых контуров, которые отличаются один от другого, по крайней мере, одной ветвью.
Порядок выполнения расчета:
- выделяют в электрической цепи ветви, независимые узлы и контуры;
- с помощью стрелок указывают произвольно выбранные положительные
направления токов в отдельных ветвях, а также указывают произвольно выбранное направление обхода контура;
- составляют уравнения по законам Кирхгофа, применяя следующее правило знаков:
а) токи, направленные к узлу цепи, записывают со знаком "плюс", а токи, направленные от узла,- со знаком "минус" (для первого закона Кирхгофа);
б) ЭДС и напряжение на резистивном элементе (RI) берутся со знаком
"плюс", если направления ЭДС и тока в ветви совпадают с направлением обхода контура, а при встречном направлении - со знаком "минус";
- решая систему уравнений, находят токи в ветвях. При решении могут
быть использованы ЭВМ, методы подстановки или определителей.
Если ток в какой-либо ветви получился отрицательным, то это показывает на то, что ранее выбранное произвольное направление тока было выбрано не верно. Это следует учитывать при построении потенциальной диаграммы, где следует знать истинное направление тока.
На рис. 1, а изображена исходная электрическая схема, для которой сле-
дует рассчитать токи в ветвях. Направления токов и обхода контуров приведны
на рис. 1, б.

а) б)
Рис.1
Система уравнений, составленных по первому и второму законам Кирхгофа, имеет вид

2.3. Расчет электрической цепи методом контурных токов.
При расчете цепи методом контурных токов выдвигаются два предполо-
жения:
- в каждом контуре протекают независимые друг от друга расчетные (контурные) токи;
- ток каждой ветви равен алгебраической сумме контурных токов, протекающих через эту ветвь.
Рассмотрим схему, представленную на рис. 2.
При расчете рекомендуется следующая последовательность действий:
- находят в цепи ветви, узлы и контуры;
- указывают произвольные направления токов в ветвях и направления об-хода контуров;
- произвольно выбирают направления контурных токов, обычно совпа-дающие с направлениями обхода контура;
- для независимых контуров составляют уравнения по второму закону
Кирхгофа относительно неизвестных контурных токов I1, I11, I111.

Для рассчитываемой электрической цепи система уравнений будет иметь
вид
для контура acef: (RI + r01 + R3) II – R3 III =E1
для контура abc: -R3 II + (R2 + R3 +R4) III - R2 IIII = -E2
для контура bdc: -R3 III + (R2 + R5 +R6) IIII = E2
В рассматриваемом примере при составлении уравнений принято во вни-
мание то, что вторая (R2, E2) и третья (Rз) ветви электрической цепи являются
смежными и по ним протекают два контурных тока, каждый из которых обу-
словливает на резисторе смежной ветви падение напряжения, например, R2III и
R2lIII (для токов второй ветви).
r01 – внутреннее сопротивление источника ЭДС Е1.
Токи в ветвях определяют алгебраическим суммированием контурных то-
ков, протекающих через ту или иную ветвь. Контурный ток берется со знаком
"плюс", если его направление совпадает с направлением тока ветви, и со знаком
"минус" - при встречном направлении.

Поиск по сайту: