 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
III. Хід роботи. з дисципліни «Економіко-математичне моделювання»
Лабораторна робота № 5
з дисципліни «Економіко-математичне моделювання»
на тему:
«ВИЗНАЧЕННЯ ГЕТЕРОСКЕДАСТИЧНОСТІ ТА АВТОКОРЕЛЯЦІЇ ЗАЛИШКІВ»
Варіант №30
Виконала:
ст. гр. ОА -32
Юнко І.С.
Прийняла:
Васильців Н. М.
Львів 2011р
Мета: набути практичних навиків при визначенні героскедантичності та автокореляції залишків; навчитись перевіряти наявність гетероскедантич-ності згідно з критерієм μ; закріпити знання, необхідні для побудови одно факторної моделі; повторити як оцінюється надійність моделі за допомогою критерію Фішера; закріпити навики перевірки наявності автокореляції за допомогою критерію Дарбіна-Уотсона; повторити як визначається прогнозне значення для моделі у випадку, якщо остання є адекватною.
I. Теоретичні відомості: Однією із передумов застосування МНК є стала величина дисперсії залишків для всіх спостережень. Така властивість називається гомоскедастичністю.
У практичних дослідженнях часто порушується умова гомоскедастичності, тобто існує явище гетероскедастичності. Якщо існує герескедастичність залишків, то це призводить до того, що оцінки параметрів економетричної моделі, знайдені за допомогою методу найменших квадратів, будуть незміщеними, обґрунтованими, але неефективними.
II. Завдання:
За даними таблиці 1 з ймовірністю 0,95, використовуючи метод найменших квадратів, необхідно:
Таблиця 1
Вихідні статистичні дані
| Періоди | Заощадження, млн. грн. (y) | Дохід, млн. грн. (x) |
| 0,66 | 8,8 | |
| 0,2 | 9,1 | |
| 0,08 | ||
| 0,2 | 10,6 | |
| 0,4 | ||
| 0,12 | 11,9 | |
| 0,71 | 12,7 | |
| 0,5 | 13,5 | |
| 0,43 | 14,3 | |
| 0,59 | 15,2 | |
| 1,2 | 16,7 | |
| 0,95 | 17,7 | |
| 1,12 | 18,6 | |
| 1,04 | 19,7 | |
| 1,53 | 21,1 | |
| 1,94 | 22,8 | |
| 1,75 | 23,9 | |
| 2,29 | 24,9 |
1) перевірити наявність гетероскедантичності згідно з критерієм μ;
2) побудувати одно факторну модель;
3) оцінити надійність моделі за допомогою критерію Фішера;
4) перевірити наявність автокореляції за допомогою критерію Дарбіна-Уотсона;
5) якщо модель адекватна згідно цих критеріїв, то визначити прогнозне значення заощаджень при величині доходів 28 млн. грн.
III. Хід роботи
1. Наявність гетероскедантичності перевіряємо за допомогою критерію μ.
Для початку нам необхідно переформувати ряд за x-ом від найменшого значення до найбільшого. Далі ми розділяємо всі вихідні статистичні дані на 3 групи по 6 елементів у кожній (див. Додаток 1). За кожною групою ми обчислюємо сума квадратів відхилень за допомогою формули:

| Sr= | 1,5636 |
Далі визначаємо суму квадратів відхилень загалом по всій сукупності спостережень за нижче вказаною формулою:
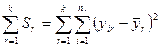 .
.
Провівши обчислення за вище вказаними формулами (див. Додаток 1) обчислюємо параметр α:
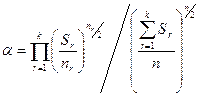
де 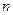 – загальна сукупність спостережень;
– загальна сукупність спостережень;
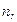 – кількість спостережень r-щї групи;
– кількість спостережень r-щї групи;
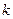 – кількість груп;
– кількість груп;
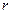 – кількість елементів у групі.
– кількість елементів у групі.
α= 0,2713
Провівши необхідні обчислення підставляємо α у нижче вказану формулу і знаходимо μ:

Ми отримаємо, що μ=2,0694, а 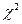 при таких умовах:
при таких умовах:
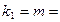 1;
1; 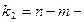 1=18-1-1=16;
1=18-1-1=16; 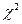 дорівнює 11,07. Отже, оскільки μ<
дорівнює 11,07. Отже, оскільки μ< 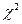 , то спостерігається не гетероскедантичність.
, то спостерігається не гетероскедантичність.
2. Для побудови однофакторної економетричної моделі
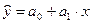
Використовується МНК, суть якого полягає у тому, що теоретична лінія повинна перебувати на оптимальній віддалі від фактичних значень, що математично виглядає наступним чином:

де 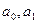 – параметри прямої, які можна знайти із системи нормальних рівнянь:
– параметри прямої, які можна знайти із системи нормальних рівнянь:
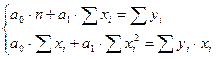
Провівши додаткові обчислення, які подані у Таблиці 2 отримаємо матриці, при множенні яких ми одержимо параметри 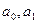 :
:
Таблиця 2
| Періоди | Заощадження, млн. грн. (y) | (y1-y1c)2 | |
| 1-а група | |||
| 0,66 | 0,1469 | ||
| 0,2 | 0,0059 | ||
| 0,08 | 0,0387 | y1c | |
| 0,2 | 0,0059 | 0,277 | |
| 0,4 | 0,0152 | ||
| 0,12 | 0,0245 | ||
| Сума | 1,66 | 0,2371 | |
| 2-а група (y2-y2c)2 | |||
| 0,71 | 0,0004 | ||
| 0,5 | 0,0529 | ||
| 0,43 | 0,0900 | у2с | |
| 0,59 | 0,0196 | 0,73 | |
| 1,2 | 0,2209 | ||
| 0,95 | 0,0484 | ||
| Сума | 4,38 | 0,4322 | |
| 3-я група (y3-y3с)2 | |||
| 1,12 | 0,2934 | ||
| 1,34 | 0,1035 | ||
| 1,53 | 0,0173 | у3с | |
| 1,94 | 0,0775 | 1,6617 | |
| 1,75 | 0,0078 | ||
| 2,29 | 0,3948 | ||
| Сума | 9,97 | 0,8943 |
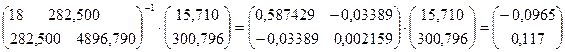
а0 = 0,0965; а1 = 0,117
3. Для того, щоб перевірити адекватність моделі використовуємо крите-
рій Фішера (за даними таблиці 3), який обчислюється за нижче вказаною формулою:
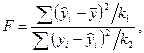
де 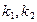 – ступені вільності, обчислені вище.
– ступені вільності, обчислені вище.
Таблиця 3
| Y-Yc | (Y-Yc)^2 | Yт | Yт-Yc | (Yт-Yc)^2 | Y-Yт | (Y-Yт)^2 |
| -0,213 | 0,045 | 0,065 | -0,807 | 0,652 | 0,595 | 0,354 |
| -0,673 | 0,453 | 0,100 | -0,772 | 0,596 | 0,100 | 0,010 |
| -0,793 | 0,629 | 0,206 | -0,667 | 0,445 | -0,126 | 0,016 |
| -0,673 | 0,453 | 0,276 | -0,597 | 0,356 | -0,076 | 0,006 |
| -0,473 | 0,224 | 0,323 | -0,550 | 0,302 | 0,077 | 0,006 |
| -0,753 | 0,567 | 0,428 | -0,444 | 0,197 | -0,308 | 0,095 |
| -0,163 | 0,027 | 0,522 | -0,351 | 0,123 | 0,188 | 0,035 |
| -0,373 | 0,139 | 0,616 | -0,257 | 0,066 | -0,116 | 0,013 |
| -0,443 | 0,196 | 0,709 | -0,163 | 0,027 | -0,279 | 0,078 |
| -0,283 | 0,080 | 0,815 | -0,058 | 0,003 | -0,225 | 0,051 |
| 0,327 | 0,107 | 0,991 | 0,118 | 0,014 | 0,209 | 0,044 |
| 0,077 | 0,006 | 1,108 | 0,235 | 0,055 | -0,158 | 0,025 |
| 0,247 | 0,061 | 1,213 | 0,340 | 0,116 | -0,093 | 0,009 |
| 0,167 | 0,028 | 1,342 | 0,469 | 0,220 | -0,302 | 0,091 |
| 0,657 | 0,432 | 1,506 | 0,633 | 0,401 | 0,024 | 0,001 |
| 1,067 | 1,139 | 1,705 | 0,832 | 0,692 | 0,235 | 0,055 |
| 0,877 | 0,770 | 1,834 | 0,961 | 0,923 | -0,084 | 0,007 |
| 1,417 | 2,009 | 1,951 | 1,078 | 1,162 | 0,339 | 0,115 |
| 0,000 | 7,362 | 15,710 | 0,000 | 6,352 | 0,000 | 1,010 |
F = 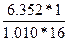 = 100,6253
= 100,6253
Отже, F= =100,6253, а 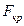 =4,49. Отже, оскільки F<F
=4,49. Отже, оскільки F<F  , то можна зробити висновок, що дана модель є адекватною, чого і слідувало очікувати внаслідок того, що даний ряд є не гетероскедантичним.
, то можна зробити висновок, що дана модель є адекватною, чого і слідувало очікувати внаслідок того, що даний ряд є не гетероскедантичним.
4. Наявність автокореляції залишків перевіряємо за допомогою критерію Дарбіна-Уотсона (обчислення здійснюються у таблиці 4), який знаходимо за формулою:

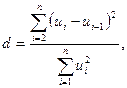
де  – залишки (відхилення).
– залишки (відхилення).
d – статистика може набувати будь-якого значення з інтервалу (0;4).
Таблиця 4
| Uі=Yі-Yті | (Yі-Yті)2 | Uі-Uі-1 | (Uі-Uі-1)2 |
| 0,595 | 0,354 | 0,595 | 0,354 |
| 0,100 | 0,010 | -0,495 | 0,245 |
| -0,126 | 0,016 | -0,225 | 0,051 |
| -0,076 | 0,006 | 0,050 | 0,002 |
| 0,077 | 0,006 | 0,153 | 0,023 |
| -0,308 | 0,095 | -0,385 | 0,149 |
| 0,188 | 0,035 | 0,496 | 0,246 |
| -0,116 | 0,013 | -0,304 | 0,092 |
| -0,279 | 0,078 | -0,164 | 0,027 |
| -0,225 | 0,051 | 0,055 | 0,003 |
| 0,209 | 0,044 | 0,434 | 0,189 |
| -0,158 | 0,025 | -0,367 | 0,135 |
| -0,093 | 0,009 | 0,065 | 0,004 |
| -0,302 | 0,091 | -0,209 | 0,044 |
| 0,024 | 0,001 | 0,326 | 0,106 |
| 0,235 | 0,055 | 0,211 | 0,044 |
| -0,084 | 0,007 | -0,319 | 0,102 |
| 0,339 | 0,115 | 0,423 | 0,179 |
| 0,000 | 1,010 | 0,339 | 1,995 |
Провівши необхідні обчислення, отримаємо, що d= =1,975135.
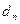 =1,39;
=1,39;
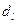 =1,16;
=1,16;
4- 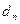 =2,61
=2,61
4- 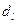 =2,84
=2,84
На рис.4 подано графічну інтерпретацію коефіцієнта Дарбіна-Уотсона

+ 1,16 1,39 2,61 2,84 -
 Оскільки,при dn = 1,39 i 4- dn = 2,61 спостерігається гіпотеза про відсутність явища автокореляції.
Оскільки,при dn = 1,39 i 4- dn = 2,61 спостерігається гіпотеза про відсутність явища автокореляції.
5. Оскільки внаслідок проведених вище обчислень встановлено, що дана
модель є адекватною статистичним даним генеральної сукупності, то ми знаходимо прогнозне значення заощаджень при величині доходів 28 млн. грн.
Хр = 28; Ур = а0 + а1 * 28 = 2,313922.
Висновок:
На даній лабораторній роботі ми набули практичних навиків при визначенні гетероскедантичності та автокореляції залишків. На онові проведених нами обчислень можна зробити висновок, що оскільки отримане нами μ<χ 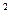 , то спостерігається не гетероскедантичність залишків, то це призводить до того, що оцінки параметрів економетричної моделі, знайдені за допомогою методу найменших квадратів (МНК), будуть зміщеними, обґрунтованими, але ефективними. Оскільки отримане нами значення F є більшим від табличного значення F
, то спостерігається не гетероскедантичність залишків, то це призводить до того, що оцінки параметрів економетричної моделі, знайдені за допомогою методу найменших квадратів (МНК), будуть зміщеними, обґрунтованими, але ефективними. Оскільки отримане нами значення F є більшим від табличного значення F 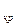 , то це свідчить про те, що дана модель є адекватною статистичним даним генеральної сукупності (чого і слідувало чекати внаслідок того, що даний ряд є не гетероскедантичним), отже дана модель може бути використана для прогнозування подальшої діяльності підприємства. На основі отриманих значень d, d
, то це свідчить про те, що дана модель є адекватною статистичним даним генеральної сукупності (чого і слідувало чекати внаслідок того, що даний ряд є не гетероскедантичним), отже дана модель може бути використана для прогнозування подальшої діяльності підприємства. На основі отриманих значень d, d 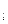 та d
та d 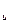 можна зробити висновок, що спостерігається відсутність автокореляції, що може бути (в даному випадку) наслідком того, що ряд є не гетероскедантичним. Ми зробили висновок, що внаслідок того, що спостерігається не гетероскедантичність і відсутність автокореляція, а також внаслідок того, що дана модель є адекватною статистичним даним, ми шукаєм прогнозне значення.
можна зробити висновок, що спостерігається відсутність автокореляції, що може бути (в даному випадку) наслідком того, що ряд є не гетероскедантичним. Ми зробили висновок, що внаслідок того, що спостерігається не гетероскедантичність і відсутність автокореляція, а також внаслідок того, що дана модель є адекватною статистичним даним, ми шукаєм прогнозне значення.
Поиск по сайту: