 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
III. Хід роботи
Лабораторна робота № 4
з дисципліни «Економіко-математичне моделювання»
на тему:
«ПОБУДОВА ЛІНІЙНОЇ БАГАТОФАКТОРНОЇ МОДЕЛІ ТА ДОСЛІДЖЕННЯ ЇЇ АДЕКВАТНОСТІ»
Варіант №30
Виконала:
ст. гр. ОА -32
Юнко І.С.
Прийняла:
Васильців Н. М.
Львів 2011р
Мета: побудувати лінійну багатофакторну модель, дослідивши її адекватність; побудувати кореляційну матрицю; використовуючи χ2 - критерій з надійністю 0.95 оцінити наявність загальної мультиколінеарності; знайти оцінки параметрів багатофакторної регресії; оцінити щільність зв’язку між результативною і факторними ознаками за допомогою коефіцієнта детермінації; перевірити адекватність побудованої моделі (критерій Фішера).
I. Теоретичні відомості: При побудові регресійного рівняння, де результуючий показник залежить від багатьох факторних ознак, слід включити в регресію всі фактори, які мають суттєвий вплив на показник у, а з другого боку необхідно визначити, як виконується умова лінійної незалежності між факторами х1, х2 …хn. Якщо між факторними ознаками існує лінійна залежність Хі =аХj, то говорять про те, що між цими факторами існує мультиколінеарність.
Мультиколінеарність означає існування тісної лінійної залежності або сильної кореляції між двома або більше пояснювальними змінними.
II. Завдання
За даними таблиці 1 з ймовірністю 0,95, використовуючи метод найменших квадратів, необхідно:
Таблиця 1
Вихідні статистичні дані
| № спосте-реження | Витрати на маркетинг, тис. грн. (х1) | Інвестиції у виробництво, тис. грн. (х2) | Сукупні витрати, тис. грн. (х3) | Доходи підприємства, тис. грн. (у) |
| 4,12 | 10,11 | 23,2 | 26,32 | |
| 4,49 | 12,64 | 24,49 | 23,10 | |
| 4,82 | 18,61 | 27,1 | 48,15 | |
| 5,23 | 15,78 | 28,25 | 41,15 | |
| 6,07 | 20,2 | 30,3 | 51,46 | |
| 5,92 | 9,56 | 31,97 | 28,97 | |
| 6,53 | 22,86 | 33,93 | 55,76 | |
| 6,57 | 12,36 | 35,52 | 34,11 | |
| 7,47 | 17,98 | 36,19 | 47,37 | |
| 7,86 | 15,36 | 36,87 | 42,29 | |
| 7,97 | 13,75 | 38,99 | 41,30 | |
| 8,3 | 18,14 | 41,05 | 32,06 | |
| 8,54 | 11,34 | 41,41 | 35,91 | |
| 9,07 | 10,45 | 42,96 | 35,57 | |
| 8,9 | 29,26 | 44,28 | 71,33 | |
| 101,860 | 238,400 | 516,510 | 614,850 |
1) побудувати кореляційну матрицю;
2) використовуючи χ2-критерій з надійністю 0.95 оцінити наявність загальної мультиколінеарності;
3) якщо існує загальна мультиколінеарність, то використовуючи t-статистику з р=0,95 виявити пари факторів, між якими існує мультиколінеарність. Якщо такі пари існують, то один із факторів необхідно вилучити;
4) знайти оцінки параметрів багатофакторної регресії;
5) оцінити щільність зв’язку між результативною і факторними ознаками за допомогою коефіцієнта детермінації;
6) перевірити адекватність побудованої моделі (критерії Фішера).
7)
III. Хід роботи
1. Будуємо кореляційну матрицю:
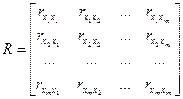 ,
,
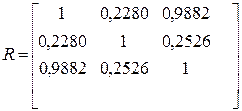
Шукаємо обернену матрицю Z=R-1
| 1,0000 | 0,2280 | 0,9882 |
| Z= 0,2280 | 1,0000 | 0,2526 |
| 0,9882 | 0,2526 | 1,0000 |

| 43,4237 | 1,0022 | -43,1631 |
| 1,0022 | 1,0913 | -1,2661 |
| -43,1631 | -1,2661 | 43,9721 |

Знаходимо визначник матриці R
R = 0,021559.
2. Для дослідження загальної мультиколінеарності знаходимо значення, та порівнюємо його з критичним значення.
 = 46,68298 n = 15; m = 3
= 46,68298 n = 15; m = 3
 кр = 7,81
кр = 7,81
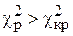 , 46,68298> 7,81, то із прийнятою надійністю можна вважати, що між факторами існує мультиколінеарність.
, 46,68298> 7,81, то із прийнятою надійністю можна вважати, що між факторами існує мультиколінеарність.
3. Щоб з`ясувати між якими факторами існує мультиколінеарність, використовуємо F– або t–статистика.
Обчислення F-критеріїв:
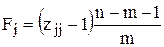 ;
;
| F1 = | 155,5537 |
| F2 = | 0,334788 |
| F3 = | 157,5644 |
Порівнявши ці значення з критичним (Fкр = 3,59), встановлено, що F1> Fкр та
F3> Fкр, тобто ці змінні незалежні мультиколінеарні з іншими.
4. Знаходимо t–статистики між двома факторами, спочатку шукаємо частинні коефіцієнти кореляції за формулою:
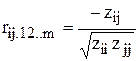 ,
,
де 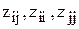 - елементи матриці Z.
- елементи матриці Z.
| r12 = | -0,14559 |
| r13 = | 0,987779 |
| r23 = | 0,182764 |
Для цих частинних коефіцієнтів знаходиться t – статистика
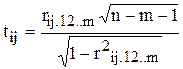 .
.
| t12 = | -0,48806 |
| t13 = | 21,01957 |
| t23 = | 0,616546 |
Фактичні значення порівнюємо з критичним значенням критерія Стьюдента  = 1,796.
= 1,796.
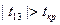 , 21,01957> 1,796 тому з надійністю р можна стверджувати, що між факторами х1 і x3 існує мультиколінеарність.
, 21,01957> 1,796 тому з надійністю р можна стверджувати, що між факторами х1 і x3 існує мультиколінеарність.
Тому ми виключаємо фактор x3 з розгляду, що узгоджується з економічною доцільністю.
В загальному випадку багатофакторна лінійна регресія має вид
 .
.
5. Оцінку параметрів 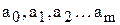 знайдемо за допомогою МНК
знайдемо за допомогою МНК
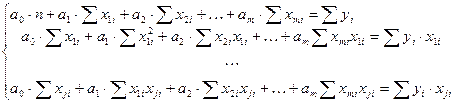


 n ∑x1 ∑x2 -1 ∑y а0
n ∑x1 ∑x2 -1 ∑y а0
∑x1 ∑x12 ∑x1* x2 × ∑y *x1 = a1
∑x2 ∑x1* x2 ∑ x22 ∑y * x2 a2
Для того щоб визначити ці параметри, необхідно знайти показники, які записуємо в таблиці 2:
Таблиця 2
| Y | X1 | X2 | X1^2 | X2^2 | X1X2 | YX1 | YX2 |
| 26,32 | 4,12 | 10,11 | 16,974 | 102,212 | 41,653 | 108,438 | 266,095 |
| 23,10 | 4,49 | 12,64 | 20,160 | 159,770 | 56,754 | 103,719 | 291,984 |
| 48,15 | 4,82 | 18,61 | 23,232 | 346,332 | 89,700 | 232,083 | 896,072 |
| 41,15 | 5,23 | 15,78 | 27,353 | 249,008 | 82,529 | 215,215 | 649,347 |
| 51,46 | 6,07 | 20,2 | 36,845 | 408,040 | 122,614 | 312,362 | 1039,492 |
| 28,97 | 5,92 | 9,56 | 35,046 | 91,394 | 56,595 | 171,502 | 276,953 |
| 55,76 | 6,53 | 22,86 | 42,641 | 522,580 | 149,276 | 364,113 | 1274,674 |
| 34,11 | 6,57 | 12,36 | 43,165 | 152,770 | 81,205 | 224,103 | 421,600 |
| 47,37 | 7,47 | 17,98 | 55,801 | 323,280 | 134,311 | 353,854 | 851,713 |
| 42,29 | 7,86 | 15,36 | 61,780 | 235,930 | 120,730 | 332,399 | 649,574 |
| 41,30 | 7,97 | 13,75 | 63,521 | 189,063 | 109,588 | 329,161 | 567,875 |
| 32,06 | 8,3 | 18,14 | 68,890 | 329,060 | 150,562 | 266,098 | 581,568 |
| 35,91 | 8,54 | 11,34 | 72,932 | 128,596 | 96,844 | 306,671 | 407,219 |
| 35,57 | 9,07 | 10,45 | 82,265 | 109,203 | 94,782 | 322,620 | 371,707 |
| 71,33 | 8,9 | 29,26 | 79,210 | 856,148 | 260,414 | 634,837 | 2087,116 |
| 614,850 | 101,860 | 238,400 | 729,815 | 4203,383 | 1647,555 | 4277,176 | 10632,988 |
| 101,86 | 238,4 | |
| 101,86 | 729,8148 | 1647,6 |
| 238,4 | 1647,555 | 4203,4 |
| 1,57264 | -0,1575 | -0,02746 |
| -0,1575 | 0,02767 | -0,00191 |
| -0,0275 | -0,0019 | 0,002545 |

 -1
-1
=
| 1,57264 | -0,1575 | -0,02746 |
| -0,1575 | 0,02767 | -0,00191 |
| -0,0275 | -0,0019 | 0,002545 |
| 614,850 |
| 4277,176 |
| 10632,988 |
| 1,29379 |
| 1,173088 |
| 1,996445 |



*
а0 = 1,29379; а1 = 1,173088; а2 = 1,996445
у = 1,29379 + 1,173088*х1+ 1,996445*х2
6. Адекватність побудованої моделі статистичним даним генеральної сукупності можна перевірити за допомогою F-критерію (критерію Фішера) за даними таблиці 3:
Таблиця 3
| Y-Yc | (Y-Yc)^2 | Yт | Yт-Yc | (Yт-Yc)^2 | Y-Yт | (Y-Yт)^2 |
| -14,670 | 215,209 | 26,311 | -14,679 | 215,474 | 0,009 | 0,000 |
| -17,890 | 320,052 | 31,796 | -9,194 | 84,529 | -8,696 | 75,621 |
| 7,160 | 51,266 | 44,102 | 3,112 | 9,684 | 4,048 | 16,387 |
| 0,160 | 0,026 | 38,933 | -2,057 | 4,232 | 2,217 | 4,915 |
| 10,470 | 109,621 | 48,743 | 7,753 | 60,103 | 2,717 | 7,384 |
| -12,020 | 144,480 | 27,324 | -13,666 | 186,746 | 1,646 | 2,708 |
| 14,770 | 218,153 | 54,593 | 13,603 | 185,036 | 1,167 | 1,362 |
| -6,880 | 47,334 | 33,677 | -7,313 | 53,479 | 0,433 | 0,187 |
| 6,380 | 40,704 | 45,953 | 4,963 | 24,630 | 1,417 | 2,008 |
| 1,300 | 1,690 | 41,180 | 0,190 | 0,036 | 1,110 | 1,233 |
| 0,310 | 0,096 | 38,094 | -2,896 | 8,384 | 3,206 | 10,276 |
| -8,930 | 79,745 | 47,246 | 6,256 | 39,137 | -15,186 | 230,612 |
| -5,080 | 25,806 | 33,952 | -7,038 | 49,538 | 1,958 | 3,835 |
| -5,420 | 29,376 | 32,797 | -8,193 | 67,133 | 2,773 | 7,692 |
| 30,340 | 920,516 | 70,150 | 29,160 | 850,320 | 1,180 | 1,392 |
| 0,000 | 2204,075 | 614,850 | 0,000 | 1838,461 | 0,000 | 365,613 |
 ,
,
F = 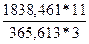 = 18,43758
= 18,43758
Fкр = 3,59 (за статистичними таблицями з ймовірністю 0,95);
18,43758 >3,59; F> Fкр. Отже модель адекватна статистичним даним генеральної сукупності.
коефіцієнт детермінації
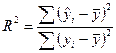 =
= 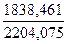 = 0,834119, отже щільність зв’язку між результативною і факторними ознаками є високою.
= 0,834119, отже щільність зв’язку між результативною і факторними ознаками є високою.
7. Знаходимо прогнозне значення:
ур = 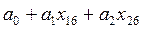 = 1,29379+ 1,173088*9+ 1,996445* 30,3 = 72,3439
= 1,29379+ 1,173088*9+ 1,996445* 30,3 = 72,3439
.
Інтервал довіри знаходять
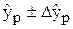 ,
,
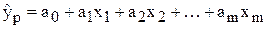 ,
,
 ,
,
де t = 1,796
 - середньоквадратичне відхилення залишків;
- середньоквадратичне відхилення залишків;
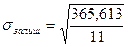 = 5,7652.
= 5,7652.
 1,796* 5,7652*
1,796* 5,7652*  = 6,254009
= 6,254009
Знаходимо інтервал довіри:
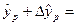 72,3439+6,254009=78,5979
72,3439+6,254009=78,5979
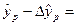 72,3439 - 6,254009= 66,0898
72,3439 - 6,254009= 66,0898
Отже, інтервал довіри для прогнозу матиме вигляд:
66,0898< 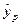 < 78,5979
< 78,5979
8. Визначаємо частинні коефіцієнти еластичності для факторів обчислюється за формулою:
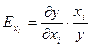
 = 1,173088*
= 1,173088*  = 0,145939
= 0,145939
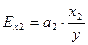 = 1,996445*
= 1,996445*  = 0,836177
= 0,836177
Частинний коефіцієнт еластичності 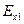 показує, як змінюється показник у, якщо фактор
показує, як змінюється показник у, якщо фактор  змінюється на 1 % при незмінних значеннях інших факторів.
змінюється на 1 % при незмінних значеннях інших факторів.
Частинний коефіцієнт еластичності  показує, як змінюється показник у, якщо фактор
показує, як змінюється показник у, якщо фактор 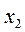 змінюється на 1 % при незмінних значеннях інших факторів.
змінюється на 1 % при незмінних значеннях інших факторів.
Висновки.
На цій лабораторній роботі я:
- дослідивши фактори впливу на у, виявила наявність мультиколінеарності між х1 та х3, тому надалі під час побудови моделі фактор х3 виключався.
- знайшла оцінки параметрів багатофакторної регресії:
а0 = 1,29379; а1 = 1,173088; а2 = 1,996445
- визначила коефіцієнт детермінації R2= 0,834119, отже щільність зв’язку між результативною і факторними ознаками є високою.
- оцінила адекватність побудованої моделі статистичним даним генеральної сукупності за допомогою критерію Фішера (оскільки 18,43758 >3,59; F> Fкр, отже модель адекватна).
- визначила прогнозне значення
ур = 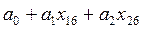 = 1,29379+ 1,173088*9+ 1,996445* 30,3 = 72,3439.
= 1,29379+ 1,173088*9+ 1,996445* 30,3 = 72,3439.
та інтервал довіри для прогнозу,який матиме вигляд:
66,0898< 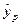 < 78,5979
< 78,5979
- визначила частинні коефіцієнти еластичності для прогнозу:
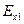 = 0,145939,
= 0,145939,  = 0,836177.
= 0,836177.
Поиск по сайту: