 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теоретичні відомості. Серед парних регресій найбільш поширеною і простою в практиці моделювання є парна лінійна регресія
Серед парних регресій найбільш поширеною і простою в практиці моделювання є парна лінійна регресія.
Парні лінійні регресійні моделі встановлюють лінійну залежність між двома змінними. При цьому одна із змінних вважається залежною змінною (у) та розглядається як функція від незалежної змінної (х). У загальному вигляді проста лінійна регресійна модель записується наступним чином
 (2.1)
(2.1)
де u – випадкові відхилення (залишки).
Для того, щоб мати явний вигляд залежності (4.1), необхідно знайти (оцінити) невідомі параметри  .
.
 (2.2)
(2.2)
Для побудови економетричної моделі використаємо метод найменших квадратів (МНК). МНК полягає у наступному: теоретична лінія повинна перебувати на оптимальній віддалі від фактичних значень. Математично
 . (2.3)
. (2.3)
де  - параметри прямої.
- параметри прямої.
Необхідною умовою існування мінімуму є рівність нулю часткових похідних функціоналу Q по 
 . (2.4)
. (2.4)
Розкриємо дужки і отримаємо систему нормальних рівнянь
 . (2.5)
. (2.5)
Невироджена система нормальних рівнянь має єдиний розв'язок, який можна знайти за формулою
 , (2.6)
, (2.6)
де  - вектор параметрів моделі;
- вектор параметрів моделі;
 - матриця статистичних даних факторної ознаки;
- матриця статистичних даних факторної ознаки;
 - вектор статистичних даних результуючої ознаки.
- вектор статистичних даних результуючої ознаки.
Щільність зв'язку між факторною і результативною ознаками можна знайти за допомогою коефіцієнта кореляції
 (2.7)
(2.7)
та коефіцієнта детермінації
 , (2.8)
, (2.8)
де  - середнє значення відповідно
- середнє значення відповідно  ;
;
 - фактичні значення і-го спостереження;
- фактичні значення і-го спостереження;
 - теоретичні значення і-го спостереження.
- теоретичні значення і-го спостереження.
Якщо  , то щільність зв'язку велика, коли
, то щільність зв'язку велика, коли  - зв'язок відсутній. Якщо
- зв'язок відсутній. Якщо 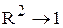 , то можна зробити висновки, що зв'язок щільний.
, то можна зробити висновки, що зв'язок щільний.
Відповідь на питання про адекватність побудованої моделі може дати критерій Фішера (F-критерій).
Для цього розраховується величина F
 (2.9)
(2.9)
де  - ступені вільності;
- ступені вільності;
m – кількість незалежних змінних;
n - кількість спостережень.
За статистичними таблицями F-розподілу з ступенями вільності k1 та k2 при заданому рівні ймовірності знаходимо значення  . Якщо
. Якщо  , то побудована регресійна модель адекватна статистичним даним генеральної сукупності. В протилежному випадку необхідно визначитися:
, то побудована регресійна модель адекватна статистичним даним генеральної сукупності. В протилежному випадку необхідно визначитися:
чи достатня статистична база;
- чи вірно обрана модель для опису економічного процесу
та провести коректування моделі.
Якщо встановлено, що із заданою ймовірністю економетрична модель адекватна спостережувальним даним і соціально-економічні умови за період прогнозування змінюються за закономірностями, що мають місце і в базовому періоді, то точкова оцінка прогнозу знаходиться за формулою
 . (2.10)
. (2.10)
Важливо також знайти інтервали довіри. Інтервали довіри – це інтервали, у які з певною заданою ймовірністю потрапляє дійсне значення залежної змінної. Такий інтервал довіри для прогнозного значення знаходимо за формулою
 , (2.11)
, (2.11)
де
 . (2.12)
. (2.12)
 (2.13)
(2.13)
Для оцінки еластичності результуючої ознаки при будь-якому значенні факторної ознаки використовується коефіцієнт еластичності
 (2.14)
(2.14)
Коефіцієнт еластичності показує, на скільки відсотків зміниться показник, якщо фактор зміниться на 1%.
Хід роботи:
1. Будуємо однофакторну модель виду у=а0+а1*х. Для цього спочатку знаходимо всі потрібні нам дані, в тому числі й параметри регресії а0 та а1.
Х=
| 2,25 | |
| 2,9 | |
| 3,29 | |
| 4,13 | |
| 5,33 | |
| 4,92 | |
| 5,79 | |
| 5,87 | |
| 7,07 | |
| 6,24 | |
| 6,87 | |
| 7,11 | |
| 7,6 | |
| 7,24 | |
| 7,86 |
Вектор статистичних даних результуючої ознаки:
У=
| 10,89 |
| 11,92 |
| 12,53 |
| 11,27 |
| 14,12 |
| 15,23 |
| 16,15 |
| 17,4 |
| 18,61 |
| 18,94 |
| 17,55 |
| 19,52 |
| 20,14 |
| 21,69 |
| 20,86 |
XТ=
| 2,25 | 2,9 | 3,29 | 4,13 | 5,33 | 4,92 | 5,79 | 5,87 | 7,07 | 6,24 | 6,87 | 7,11 | 7,6 | 7,24 | 7,86 |
| ХТ*Х= |
| ||||||
(ХТ*Х)-1=
| |||||||
| ХТ*У= |
| ||||||
| (ХТ*Х)-1* ХТ*У =A= |
| |||
уt=5,678008+1,913696*х
2. Перевіряємо щільність зв’язку між факторами за допомогою коефіцієнта кореляції та коефіцієнта детермінації.
Необхідні для цього дані наведені нижче:
| Yi-Yc | (Yi-Yc)^2 | Xi-Xc | (Xi-Xc)*(Yi-Yc) | (Xi-Xc)^2 |
| -5,56467 | 30,96552 | -3,381333333 | 18,81599289 | 11,43342 |
| -4,53467 | 20,5632 | -2,731333333 | 12,38568622 | 7,460182 |
| -3,92467 | 15,40301 | -2,341333333 | 9,188952889 | 5,481842 |
| -5,18467 | 26,88077 | -1,501333333 | 7,783912889 | 2,254002 |
| -2,33467 | 5,450668 | -0,301333333 | 0,703512889 | 0,090802 |
| -1,22467 | 1,499808 | -0,711333333 | 0,871146222 | 0,505995 |
| -0,30467 | 0,092822 | 0,158666667 | -0,04834044 | 0,025175 |
| 0,945333 | 0,893655 | 0,238666667 | 0,225619556 | 0,056962 |
| 2,155333 | 4,645462 | 1,438666667 | 3,100806222 | 2,069762 |
| 2,485333 | 6,176882 | 0,608666667 | 1,512739556 | 0,370475 |
| 1,095333 | 1,199755 | 1,238666667 | 1,356752889 | 1,534295 |
| 3,065333 | 9,396268 | 1,478666667 | 4,532606222 | 2,186455 |
| 3,685333 | 13,58168 | 1,968666667 | 7,255192889 | 3,875648 |
| 5,235333 | 27,40872 | 1,608666667 | 8,421906222 | 2,587808 |
| 4,405333 | 19,40696 | 2,228666667 | 9,818019556 | 4,966955 |
| 183,5652 | 85,92450667 | 44,89977 |
Коефіцієнт кореляції становить:
| rxy = 85,92450667/90,78565= 0,946455 |
| rxy= 0,946455 |
Розраховую коефіцієнт детермінації. Дані для цього наведені нижче.
| Y^ | Y^-Yc | (Y^-Yc)^2 | Yi-Y^ | (Yi-Y^)^2 | |
| 9,983823 | -6,470843324 | 41,87181 | 0,906177 | 0,821156 | |
| 11,22773 | -5,226941069 | 27,32091 | 0,692274 | 0,479244 | |
| 11,97407 | -4,480599715 | 20,07577 | 0,555933 | 0,309062 | |
| 13,58157 | -2,873095262 | 8,254676 | -2,31157 | 5,343362 | |
| 15,87801 | -0,576660328 | 0,332537 | -1,75801 | 3,090586 | |
| 15,09339 | -1,361275597 | 1,853071 | 0,136609 | 0,018662 | |
| 16,75831 | 0,30363973 | 0,092197 | -0,60831 | 0,370037 | |
| 16,9114 | 0,456735392 | 0,208607 | 0,488598 | 0,238728 | |
| 19,20784 | 2,753170326 | 7,579947 | -0,59784 | 0,357409 | |
| 17,61947 | 1,16480283 | 1,356766 | 1,320531 | 1,743801 | |
| 18,8251 | 2,370431171 | 5,618944 | -1,2751 | 1,625874 | |
| 19,28438 | 2,829718157 | 8,007305 | 0,235615 | 0,055515 | |
| 20,2221 | 3,767429089 | 14,19352 | -0,0821 | 0,00674 | |
| 19,53317 | 3,078498608 | 9,477154 | 2,156835 | 4,651936 | |
| 20,71966 | 4,264989991 | 18,19014 | 0,140343 | 0,019696 | |
| 164,4334 | 19,13181 |
R2= 164,4334/19,13181
R2= 0,897345 – коефіцієнт детермінації
Коефіцієнти детермінації і кореляції наближаються до одиниці, значить щільність зв’язку велика.
3. Оцінюю надійність моделі за допомогою критерію Фішера.
1. Оцінюю надійність моделі за допомогою критерію Фішера.
Здійснивши розрахунки знаходжу критерій Фішера:
F= 11,64509
F>Fкр 11,64509 >4,67 значить побудована регресійна модель адекватна статистичним даним генеральної сукупності.
Оцінка прогнозу знаходжу за формулою 2.10. ур= 21,37031
2. Знаходжу прогнозне значення та інтервал довіри для прогнозу.
σзал= 1,213127
t= 2,16
∆ŷр= 2,886695
Отже, інтервал довіри має вигляд 18,48362 ≤ у ≤ 24,25701
3. Визначаю коефіцієнт еластичності в точці прогнозу.
E= 5,678008*16/(5,678008+1,913696*16)= 2,5029
Оскільки коефіцієнт еластичності становить 2,5029, то при зміні фактора на 1% показник зміниться на 2,5029%.
4. Навести графічну інтерпретацію моделі.

Висновок: на цій лабораторній роботі, я навчився будувати лінійну економетричну модель виду у=а0+а1*х та досліджувати її адекватність. В процесі даної роботи я перевірив істотність зв’язку між факторами за допомогою коефіцієнта кореляції і коефіцієнта детермінації; оцінив надійність моделі за допомогою критерію Фішера, знайшов прогнозне значення та інтервал довіри для прогнозу, визначив коефіцієнт еластичності в точці прогнозу та навів графічну інтерпретацію моделі.
Поиск по сайту: