Контрольная работа №1

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КОНТРОЛЬНЫЕ ЗАДАНИЯ

ДЛЯ КОНТРОЛЬНЫХ РАБОТ №1

По курсу

“ ИНФОРМАТИКА И ПРОГРАММИРОВАНИЕ”

(для студентов заочного отделения

Направления 090303)

Ростов – на – Дону, 2015

Кафедра «Информатика»

Составитель: проф. Рашидова Е.В.

Задания контрольных работ по курсу «Информатика и программирование» (для студентов заочного отделения направления 090303). — ДГТУ, Ростов- на-Дону, 2015,

10 с.

Методические указания содержат варианты контрольных работ по курсу «Информатика и программирование» для студентов заочного отделения.

Печатается по решению методической комиссии факультета «Информатика и вычислительная техника»

Рецензент д-р тех. наук Б.В. Соболь

© ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ, 2015

Контрольная работа №1

Варианты выполнения контрольных работ определяются номером последней цифры зачетной книжки. Если номер зачетной книжки оканчивается на цифру 0, то брать 10 вариант.

Вариант №1

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 10010011111,101₂; 1372,12₈; 3CA,7D₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1802; 286,06.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 1263,71₈; 2BA,2C₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=100101,101₂; Y=11101,11₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=100101,011₂; Y=110,1₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -100101; Y=11101

4. Даны x, y и z. Вычислите a, b, если: a = 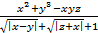; b = .

5. Даны два действительных числа. Выведите первое число, если оно не больше второго, или их произведение в противном случае.

6. Даны натуральное n, действительное x. Вычислите: sin x + sin²x+ … + sinⁿx.

7. Теоретические вопросы:

1. Понятие информации. Свойства информации. Количество информации.

2.Функциональная организация персонального компьютера: центральный процессор.

Вариант №2

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 11100101010,011₂; 2136,31₈; 1C3,А2₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1731; 476,91.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 3472,62₈; 4СA,27₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=101101,101₂; Y=1101,111₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=110000,11₂; Y=110,1₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -101101; Y=1101.

4. Даны x, y и z. Вычислите a, b, если: a = ; b = 4 - .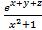

5. Даны два действительных числа. Замените первое число нулем, если оно не меньше второго, иначе оставить без изменения.

6. Даны натуральное n, действительное x. Вычислите: sin x + sin x²+ … + sin xⁿ.

7. Теоретические вопросы:

1.Информационные процессы. Информация в жизни человека.

2.Функциональная организация персонального компьютера: оперативное запоминающее устройство.

Вариант №3

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 11001100111,011₂; 1742,36₈; 123Е,4D₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1660; 438,76.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 1724,31₈; 2AF,3C₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=110101,101₂; Y=11101,11₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=111001,0001₂; Y=1010,011₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -110101; Y=11101.

4. Даны x, y и z. Вычислите a, b, если: a = 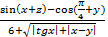; b = cos⁴ (.

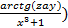5. Даны два действительных числа a, b (a≠b). Меньшее из них замените их полусуммой, а большее – их удвоенным произведением.

6. Даны натуральное n, действительное x. Вычислите:

sin x + sin(sin x)+ … +sin(sin(sin x))+sin(sin(…sin x)…).

7. Теоретические вопросы:

1.Представление (кодирование) данных.

2. Функциональная организация персонального компьютера: внутренние шины передачи информации.

Вариант №4

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 11101011101,1001₂; 1467,63₈; 1AF,73₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1589; 362,87.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 1273,56₈; 30A,E0F₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=1101111,101₂; Y=10101,11₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=111011,0001₂; Y=101,01₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -1101111; Y=10101.

4. Даны x, y и z. Вычислите a, b, если: a = ln 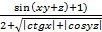; b = 3a³+ 4x²- a + 5.

5. Даны действительные числа a, b, c. Выясните, существует ли треугольник с длинами сторон a, b, c.

6. Дано натуральное число n. Сколько цифр в числе n?

7. Теоретические вопросы:

1. Системы счисления. Десятичная, двоичная, восьмеричная, шестнадцатеричная системы счисления. Представление чисел. Перевод чисел из одной системы в другую.

2.Внешние запоминающие устройства.

Вариант №5

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 101011010110,001₂; 1523,24₈; 2A7,3E₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1518; 305,37.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 1623,72₈; 5C2,C7₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=1000111,11₂; Y=11101,111₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=111100,011₂; Y=101,11₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -1000111; Y=11101.

4. Даны x, y и z. Вычислите a, b, если: a = 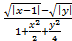; b = x(arctg(z)+e).

5. Даны действительные числа a, b, c (a ≠ 0). Найдите действительные корни уравнения = 0 или выдайте сообщение, что действительных корней нет.

6. Дано натуральное число n. Чему равна сумма его цифр?

7. Теоретические вопросы:

1.Структуры данных. Хранение данных. Файл. Имя файла. Каталоги (папки).

2.Внешние устройства: видеотерминалы, устройства ручного ввода, устройства печати.

Вариант №6

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 11001100011,1001₂; 1273,56₈; 30A,E0F₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1682; 324,93.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 12372,41₈; 1D2,7D₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=1110001,101₂; Y=10011,11₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=110110,101₂; Y=100,11₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -1110001; Y=10011.

4. Даны x, y и z. Вычислите a, b, если: a = 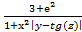; b = 1+ .

5. Дано действительное число x. Вычислите y(x), если: y=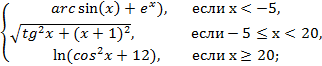

6. Дано натуральное число n. Найдите первую цифру числа n.

7. Теоретические вопросы:

1.Представление информации в технических устройствах. Базовая система элементов компьютера.

2.Устройства обработки звуковой информации. Устройства для соединения компьютеров в сеть.

Вариант №7

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 10011010111,011₂; 1623,72₈; 5C2,C7₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1846; 457,21.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 1735,12₈; 5AD,4D₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=1010001,101₂; Y=10011,11₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=100110,0001₂; Y=111,01₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -1010001; Y=10011.

4. Даны x, y и z. Вычислите a, b, если: a = 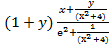; b = .

5. Дано действительное число x. Вычислите y(x), если: y=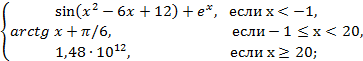

6. Даны натуральные числа n, m. Получите сумму m последних цифр числа n.

7. Теоретические вопросы:

1.Функциональные узлы компьютерных систем: элемент памяти, регистры, устройства обработки информации.

2.Системное программное обеспечение (ПО). Базовое ПО. Операционные системы. Файло­вые системы.

Вариант №8

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 11000001111,011₂; 1735,66₈; 23A,EF₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 2010; 343,43.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 2451,23₈; 2BA,D3₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=1000011,101₂; Y=10011,011₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=101011,111₂; Y=110,11₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -1000011; Y=10011.

4. Даны x, y и z. Вычислите a, b, если: a = ; b = .

5. Дано действительное число x. Вычислите y(x), если: y=

6. Дано натуральное число n. Входит ли цифра 3 в запись числа n²?

7. Теоретические вопросы:

1.Принцип автоматической обработки информации вычислительным устройством.

2.Служебные программы: файловые менеджеры, архиваторы, программы резервирования данных, записи компакт-дисков, просмотра и конвертации.

Вариант №9

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 10000111111,1001₂; 1327,46₈; 3CD,BA₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1933; 381,93.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 1372,12₈; 3CA,7D₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=1101001,101₂; Y=10111,11₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=1010110,101₂; Y=1000,01₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -1101001; Y=10111.

4. Даны x, y и z. Вычислите a, b, если: a = ; b = .

5. Дано действительное число x. Вычислите y(x), если: y=

6. Дано число m > 0. Найдите наибольшее целое k, такое, что 4^k < m.

7. Теоретические вопросы:

1.Поколения цифровых устройств обработки информации.

2.Прикладное программное обеспечение (ППО). Классификация ППО, ППО общего назначения, ППО специального назначения.

Вариант №10

1. 1) Переведите числа в 10-ю систему счисления (с.с.): 11100001101,011₂; 1523,74₈; 4BA,2F₁₆.

2) Переведите десятичные числа во 2-ю, 8-ю и 16-ю с.с.: 1856; 419,96.

3) Переведите восьмеричное число в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с.: 2136,31₈; 1C3,A2₁₆.

2. 1) Заданы двоичные числа Х и Y. Вычислить Х+Y и Х–Y, если: Х=1010001,101₂; Y=1111,011₂.

2) Заданы двоичные числа Х и Y. Вычислить Х*Y и Х/Y, если: Х=111111,01₂; Y=101,1₂.

3. 1) Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики.

2) Измените число Y, добавив в конец числа две единицы («11»). Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Х= -1010001; Y=1111.

4. Даны x, y и z. Вычислите a, b, если: a = ; b = .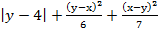

5. Дано действительное число x. Вычислите y(x), если: y=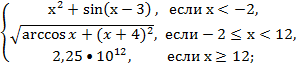

6. Дано натуральное число n. Найдите наименьшее число вида 2^К, превосходящее n.

7. Теоретические вопросы:

1.Архитектуры вычислительных систем сосредоточенной обработки информации.

2.Понятие алгоритма и его свойства. Способы описания алгоритмов. Основные алгоритмические конструкции.

Литература

1. Информатика: учебник / Б.В. Соболь [и др.] – Ростов н/Д: Феникс, 2010. – 448.

2. Практикум по высшей математике / Б.В. Соболь [и др.] – Ростов н/Д: Феникс, 2006. – 448.

Поиск по сайту: