Еселі интегралдар

1/4

$$$ 72

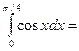
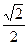
$$$ 73

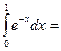
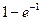
$$$ 74

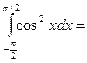
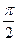
$$$ 75

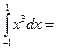
$$$ 76

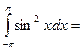
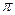
$$$ 77

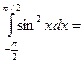
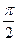
$$$ 78

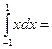
$$$ 79

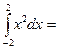
16/3

$$$ 80

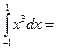
$$$ 81

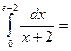
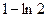
$$$ 82

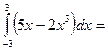
$$$ 83

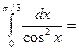
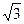
$$$ 84

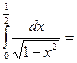
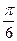
$$$ 85

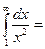
$$$ 101

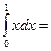
1/2

$$$ 102

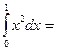
1/3

$$$ 103

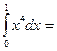
1/5

$$$ 104

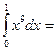
1/10

$$$ 105

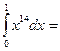
1/15

$$$ 106

1/3

$$ 107

$$$ 108

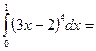
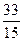
$$$ 109

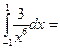
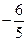
$$$ 110

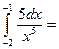
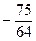
$$$ 111

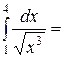
$$$ 112

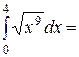
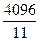
$$$ 113

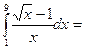
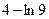
$$$ 114

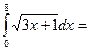
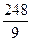
$$$ 115

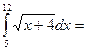
74/3

$$$ 116

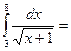
$$$ 117

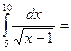
$$$ 118

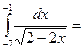
$$$ 119

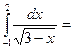
$$$ 120

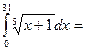
105/2

$$$ 121

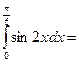
1/4

$$$ 122

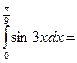
1/6

$$$ 123

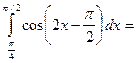
1/2

$$$ 124

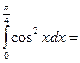
$$$ 125

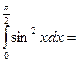
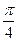
$$$ 126

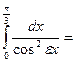
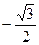
$$$ 127

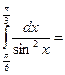
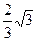
$$$ 128

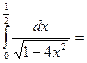
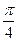
$$$ 129

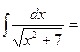
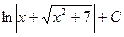
$$$ 130

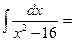
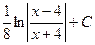
$$$ 131

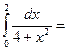
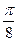
$$$ 132

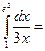
2/3

$$$ 133

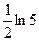
$$$ 134

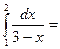
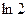
$$$ 135

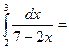
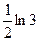
$$$ 136

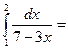
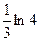
$$$ 137

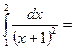
1/6

$$$ 138

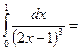
$$$ 139

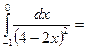
1/24

$$$ 140

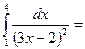
3/10

$$$ 141

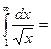
жинақсыз

$$$ 142

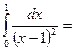
жинақсыз

$$$ 143

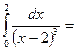
жинақсыз

$$$ 144

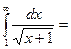
жинақсыз

$$$ 145

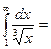
жинақсыз

$$$ 149

анықталмаған интегралын есептеңіз:

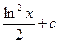
$$$ 150

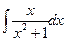анықталмаған интегралын есептеңіз:

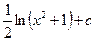
$$$ 8

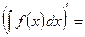
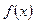
$$$ 5

Егер болса, онда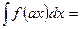

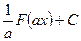
$$$ 6

Егер болса, онда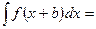

$$$ 7

Егер болса, онда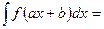

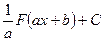
$$$ 9

Егер болса, онда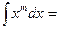

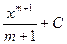
$$$ 10

Егер 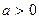, болса, онда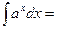

$$$ 12

Егер 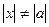болса, онда

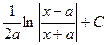
$$$ 13

Егер болса, онда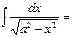

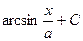
$$$ 14

Егер - дифференциалданатын функциялар болса, онда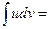

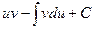
$$$ 22

Егер 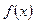функциясы 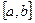кесіндісінде интегралданса және теңсіздігі орындалса, онда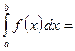

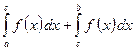
$$$ 23

Егер 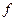, функциялары 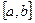кесіндісінде интегралданса және , онда

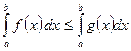
$$$ 24

Егер 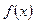функциясы 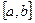кесіндісінде үзіліссіз болса және 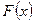оның қайсыбір алғашқы функциясы болса, онда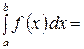

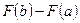
$$$ 25

Егер 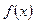функциясы жұп болса, онда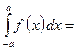

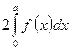
$$$ 26

Егер 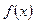функциясы тақ болса, онда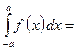

$$$ 28

Егер 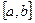кесіндісінде параметрлік теңдеумен берілген 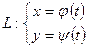қисығында , функциялары үзіліссіз болса, онда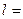

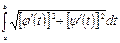
$$$ 29

Егер қисығы теңдеуімен берілсе, онда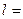

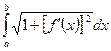
$$$ 30

Егер қисығы поляр координат жүйесінде , 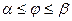теңдеуімен берілсе, онда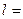

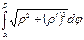
$$$ 31

Егер кесіндісінде 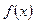функциясының таңбалары шектеулі рет ауысса, онда , , , сызықтарымен қоршалған жазық фигурасының ауданы былай есептелінеді:

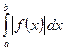
$$$ 34

Параметрлік теңдеумен берілген сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:

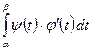
$$$ 20

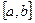кесіндісіндегі 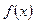функциясының анықталған интегралы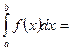

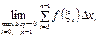
$$$ 32

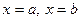, , сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:

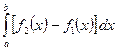
$$$ 35

қисығын () өсімен айналдырғаннан пайда болған дененіің көлемі былай есептелінеді

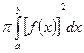
$$$ 86

, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек

1/3

$$$ 87

, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек

1/4

$$$ 88

, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек

8/3

$$$ 89

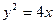, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек

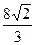
$$$ 33

сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:

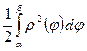
$$$ 90

сызығымен қоршалған жазық фигураның ауданын есептеу керек

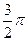
$$$ 91

сызығымен қоршалған жазық фигураның ауданын есептеу керек

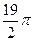
$$$ 92

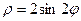сызығымен қоршалған жазық фигураның ауданын есептеу керек

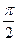
$$$ 93

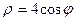сызығымен қоршалған жазық фигураның ауданын есептеу керек

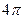
$$$ 97

сызығымен қоршалған жазық фигураның ауданын есептеу керек

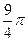
$$$ 98

қисығының доғасының ұзындығын есептеу керек

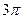
$$$ 99

қисығының доғасының ұзындығын есептеу керек

$$$ 100

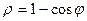қисығының доғасының ұзындығын есептеу керек

$$$ 94

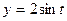, сызығымен қоршалған жазық фигураның ауданын есептеу керек

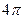
$$$ 95

, сызығымен қоршалған жазық фигураның ауданын есептеу керек

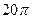
$$$ 96

, сызығымен қоршалған жазық фигураның ауданын есептеу керек

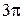
$$$ 146

, қисығының доғасының ұзындығын есептеу керек

$$$ 148

, қисығының доғасының ұзындығын есептеу керек

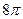
$$$ 147

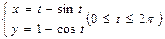қисығының доғасының ұзындығын есептеу керек

Қатар

$$$ 158

Ауыспа таңбалы қатарының жинақты болу шартын көрсетіңіз

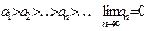
$$$ 207

Гармоникалық қатарды көрсетіңіз

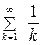
$$$ 157

Дәрежелік қатардың жинақтылық радиусын көрсетіңіз

$$$ 165

Егер сандық қатар жинақты болса, онда

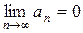
$$$ 166

қатарының абсолют жинақты болу шартын көрсетіңіз

қатар жинақты

$$$ 167

Егер және қатарларының мүшелері үшін теңсіздіктер орындалса, онда

қатарының жинақтылығынан 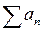қатардың жинақтылығы шығады

$$$ 170

Егер болса, онда 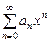дәрежелік қатарының жинақтылық радиусы неге тең?

$$$ 172

Егер дәрежелік қатары нөлге тең емес 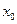нүктесінде жинақты болса, онда

теңсіздігін қанағаттандыратын барлық -тер үшін қатар абсолют жинақты болады

$$$ 173

Егер дәрежелік - қатары 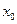нүктесінде жинақсыз болса, онда ол

теңсіздігін қанағаттандыратын барлық -тер үшін жинақсыз болады

$$$ 241

Егер қатары жинақты болса, онда қатары туралы не айтуға болады?

Жинақты

$$$ 243

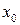Егер қатары нүктесінде жинақты болса, онда қатар

болғанда әрбір нүктесінде абсолют жинақты

$$$ 154

Қатар жинақтылығының Коши белгісін көрсетіңіз

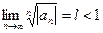
$$$ 156

Қатар жинақтылығының Даламбер белгісін көрсетіңіз

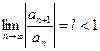
$$$ 219

Қатар жинақты деп аталады, егер

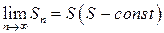
$$$ 169

Мына , () сандық қатары үшін дұрыс тұжырымды көрсетіңіз

болса қатар жинақты

$$$ 164

Функциялық қатарды көрсетіңіз

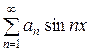
$$$ 174

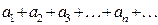қатарының шартты жинақты болуының анықтамасы

қатар жинақсыз болып, ал қатар жинақты болса

$$$ 159

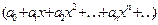дәрежелік қатардың жинақтылық радиусын көрсетіңіз

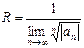
$$$ 162

функциясының Маклорен қатарына жіктелуін көрсетіңіз

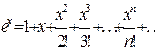
$$$ 161

функциясының Маклорен қатарына жіктелуін көрсетіңіз

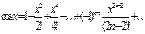
$$$ 163

функциясының нүктесінде Тейлор қатарына жіктелуін көрсетіңіз

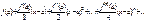
$$$ 171

функциясының дәрежелік қатарға жіктелуін көрсетіңіз

,

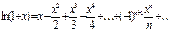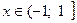
$$$ 211

функциясы үшін Маклорен қатарының жалпы мүшесі

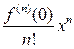
$$$ 208

p – параметрінің қандай мәндерінде - Дирихле қатары жинақты болады?

$$$ 153

параметрінің қандай мәндерінде қатары жинақты?

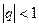
$$$ 160

функциясының Маклорен қатарына жіктелуін көрсетіңіз

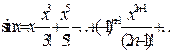
$$$ 186

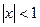, , қатарының қосындысын табу керек

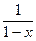
$$$ 187

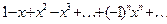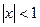, қатарының қосындысын табу керек

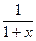
$$$ 223

қатарын жинақтылыққа зерттеңіз

жинақты

$$$ 224

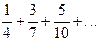қатарының жалпы мүшесін табыңыз

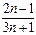
$$$ 225

қатарының қосындысын табыңыз

1/3

$$$ 199

қатардың жалпы мүшесін табыңыз

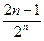
$$$ 217

қатарының жинақтылыққа зертте

жинақты

$$$ 200

қатардың жалпы мүшесін табыңыз

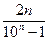
$$$ 237

қатарының жалпы мүшесін табыңыз

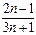
$$$ 238

қатарының жалпы мүшесін табыңыз

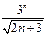
$$$ 239

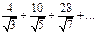қатарының жалпы мүшесін табыңыз

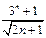
$$$ 240

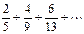қатарының жалпы мүшесін табыңыз

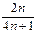
$$$ 175

функциясының Маклорен қатарына жіктелуін көрсетіңіз ( -кез келген тұрақты сан)

,

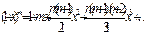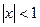
$$$ 151

- қатарының жинақты болуының қажетті шартын көрсетіңіз

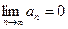
$$$ 152

қатарының жинақсыз болуының жеткілікті шартын көрсетіңіз

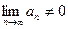
$$$ 155

гармоникалық қатары қандай болады?

жинақсыз

$$$ 168

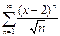қатарының жинақтылық аймағын табыңыз

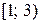
$$$ 176

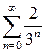қатарының қосындысын табыңыз

$$$ 177

қатарды жинақтылыққа зерттеңіз

жинақсыз

$$$ 178

қатардың жинақтылық аймағын табыңыз

[-3, 3)

$$$ 179

қатардың жинақтылық аймағын табыңыз

(-1,5)

$$$ 180

қатардың жинақтылық радиусын табыңыз

1/6

$$$ 181

қатардың жинақтылық радиусын табыңыз

+

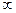
$$$ 182

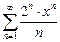қатардың жинақтылық аймағын табыңыз

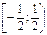
$$$ 183

қатардың жинақтылық аймағын табыңыз

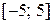
$$$ 184

қатардың жинақтылық аймағын табыңыз

(4,5; 5,5)

$$$ 185

қатардың жинақтылық аймағын табыңыз

(-1,5; -0,5)

$$$ 188

қатарын жинақтылыққа зерттеңіз

жинақсыз

$$$ 189

қатарын жинақтылыққа зерттеңіз

жинақсыз

$$$ 190

қатарының жинақтылыққа зерттеңіз

жинақты

$$$ 191

қатардың төртiншi мүшесiн табыңыз

1/17

$$$ 192

қатардың төртiншi мүшесiн табыңыз

1/16

$$$ 193

қатардың бесінші мүшесiн табыңыз

10/13

$$$ 194

қатарының алғашқы екі мүшесінің қосындысын табыңыз

19/84

$$$ 195

қатарының алғашқы екі мүшесінің қосындысын табыңыз

9/8

$$$ 196

қатарының алғашқы екі мүшесінің қосындысын табыңыз

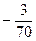
$$$ 197

қатарының алғашқы екі мүшесінің қосындысын табыңыз

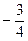
$$$ 198

қатарының үшінші және бесінші мүшелерінің қосындысын табыңыз

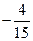
$$$ 201

қатарды жинақтылыққа зерттеңіз

абсолютті жинақталады

$$$ 202

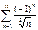қатарды жинақтылыққа зерттеңіз

шартты жинақталады

$$$ 203

қатардың жинақтылық радиусын табыңыз

$$$ 204

қатарын жинақтылыққа зерттеніз

жинақты

$$$ 205

қатарды жинақтылыққа зерттеңіз

жинақты

$$$ 206

қатарды жинақтылыққа зерттеңіз

жинақты

$$$ 209

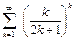қатарын жинақтылыққа зерттеңіз

жинақты

$$$ 210

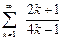қатарын жинақтылыққа зерттеңіз

жинақсыз

$$$ 212

қатарының жинақтылық аралығын табыңыз

(–2,2)

$$$ 213

қатарының жинақтылық радиусын тап

$$$ 214

қатарының жинақтылық радиусын тап

1/3

$$$ 215

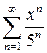қатарының жинақтылық радиусын тап

$$$ 216

қатарының және мүшелерінің қосындысын табыңыз

2/15

$$$ 218

қатарының жинақталу интервалын табыңыз

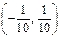
$$$ 220

қатарының жинақтылық интервалын табыңыз

(-2; 0)

$$$ 221

қатарының жинақтылық интервалын табыңыз

(1; 3)

$$$ 222

қатарының жинақтылық интервалын табыңыз

(-1; 1)

$$$ 226

қатарының қосындысын табыңыз

0,5

$$$ 227

қатарының қосындысын табыңыз

0,5

$$$ 228

қатарының бірінші және үшінші мүшелерінің айырымын табыңыз

$$$ 229

қатарының бірінші және үшінші мүшелерінің қосындысын табыңыз

17,25

$$$ 230

қатарының қосындысын табыңыз

$$$ 231

қатарының алғашқы екі мүшесінің қосындысын табыңыз

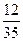
$$$ 232

қатарының алғашқы үш мүшесінің қосындысын табыңыз

69/140

$$$ 233

дәрежелік қатардың жинақтылық радиусын табыңыз

$$$ 234

дәрежелік қатардың жинақтылық радиусын табыңыз

5/3

$$$ 235

қатарының қосындысын табыңыз

5/6

$$$ 236

дәрежелік қатардың жинақталу радиусын табыңыз

$$$ 242

және қатарлары жинақты, онда 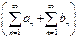қатары туралы не айтуға болады

жинақты

$$$ 244

қатарының екінші және төртінші мүшелерінің қосындысын табыңыз

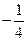
$$$ 245

қатарының екінші және үшінші мүшелерінің қосындысын табыңыз

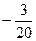
$$$ 246

қатарының екінші және үшінші мүшелерінің қосындысын табыңыз

-1

$$$ 247

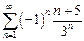қатарының екінші және үшінші мүшелерінің қосындысын табыңыз

13/27

$$$ 248

қатарының алғашқы үш мүшесі мынадай:

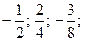
$$$ 249

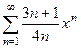қатарының жинақтылық радиусы тең

$$$ 250

ауыспалы таңбалы қатары жинақты және оның қосындысы - ке тең болса, онда

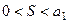
Еселі интегралдар

$$$ 270

Біртекті пластинканың массасы былай табылады:

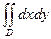
$$$ 251

Егер интегралында алмастыруын жасасақ, онда көшу Якобианы неге тең?

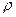
$$$ 252

Егер , мұндағы және 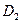аймақтарының шекаралары ортақ, онда

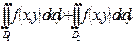
$$$ 255

Егер болса, онда

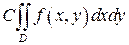
$$$ 256

Егер функциясы аймағында үзіліссіз болса, онда екі еселі интеграл нені білдіреді?

табаны болатын цилиндрдің көлемін

$$$ 258

Егер облысы , , 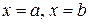мұндағы 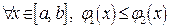, қисықтарымен шектелген және функциялары кесіндісінде үзіліссіз болса, онда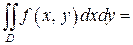

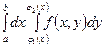
$$$ 259

Егер аймағы , , мұндағы қисықтарымен шектелген және функциялары кесіндісінде үзіліссіз болса, онда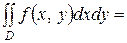

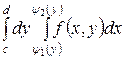
$$$ 267

Егер , онда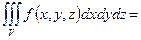

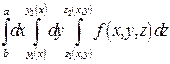
$$$ 269

Егер интегралдау аймағы тік бұрышты параллелипипед болса, онда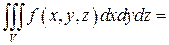

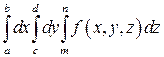
$$$ 301

Интегралды есептеңіз: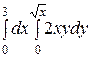

$$$ 302

Интегралды есептеңіз: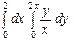

$$$ 303

Интегралды есептеңіз:

$$$ 304

Интегралды есептеңіз: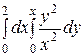

2/3

$$$ 305

Интегралды есептеңіз: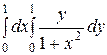

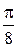
$$$ 306

Интегралды есептеңіз: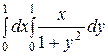

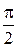
$$$ 307

Интегралды есептеңіз: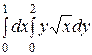

4/3

$$$ 312

Интегралды есептеңіз: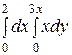

$$$ 313

Интегралды есептеңіз: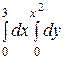

$$$ 314

Интегралды есептеңіз: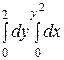

8/3

$$$ 315

Интегралды есептеңіз:

$$$ 319

Интегралды есептеңіз: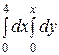

$$$ 320

Интегралды есептеңіз: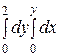

$$$ 321

Интегралды есептеңіз: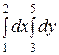

$$$ 322

Интегралды есептеңіз:

$$$ 323

Интегралды есептеңіз:

$$$ 324

Интегралды есептеңіз: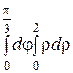

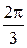
$$$ 325

Интегралды есептеңіз: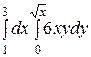

$$$ 326

Интегралды есептеңіз: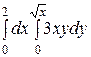

$$$ 330

Интегралды есептеңіз: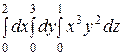

$$$ 331

Интегралды есептеңіз: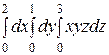

9/2

$$$ 332

Интегралды есептеңіз: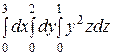

$$$ 333

Интегралды есептеңіз: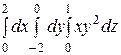

16/3

$$$ 334

Интегралды есептеңіз: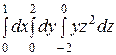

16/3

$$$ 335

Интегралды есептеңіз: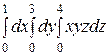

$$$ 336

Интегралды есептеңіз: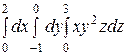

$$$ 337

Интегралды есептеңіз: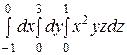

3/4

$$$ 338

Интегралды есептеңіз: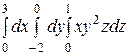

$$$ 339

Интегралды есептеңіз: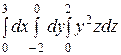

$$$ 340

Интегралды есептеңіз: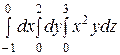

$$$ 341

Интегралды есептеңіз: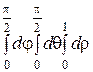

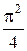
$$$ 342

Интегралды есептеңіз: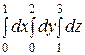

$$$ 343

Интегралды есептеңіз: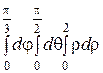

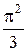
$$$ 344

Интегралды есептеңіз: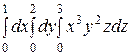

$$$ 345

Интегралды есептеңіз: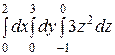

$$$ 346

Интегралды есептеңіз: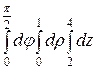

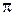
$$$ 347

Интегралды есептеңіз: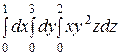

$$$ 348

Поиск по сайту: