 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Контрольная работа. В цепи рис.1 ЭДС источника Е= 12 В, сопротивления равны R 1, R2, R3, R4, R5, внутреннее сопротивление источника R вт
Задача № 1

Рисунок 1.
В цепи рис.1 ЭДС источника Е= 12 В, сопротивления равны R 1, R2, R3, R4, R5, внутреннее сопротивление источника R вт.
Определить токи в ветвях цепи преобразованием звезды сопротивлений R1, R2, R3 в эквивалентный треугольник.
| Но-мер вари-анта | Данные к задаче № 1 | Ном-мер вари-анта | Данные к задаче № 1 | ||||||||||
| Rвт Ом | R1 Ом | R2 Ом | R3 Ом | R4 Ом | R5 Ом | Rвт Ом | R1 Ом | R2 Ом | R3 Ом | R4 Ом | R5 Ом | ||
Задача № 2
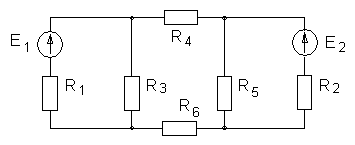
Рисунок 2.
В цепи рис.2 ЭДС источников питания равны Е1, Е2, а сопротивления ветвей – R1, R2, R3, R4, R5, R6. Определить методом непосредственного применения законов Кирхгофа токи в ветвях цепи и режим работы каждого из источников. Составить баланс мощностей.
| Номер варианта | Данные к задаче № 2 | |||||||
| Е1, В | Е2, В | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | |
Задача № 3

Рисунок 3.
В цепи рис. 3 ЭДС источников питания Е1, Е2, Е3, J = 1 А, а сопротивления ветвей соответственно R1, R2, R3, R4 (включая внутренние сопротивления источников питания) и т.д. Определить токи в ветвях цепи и режим работы каждого из источников. Задачу решить методом узловых потенциалов.
| Номер варианта | Данные к задаче № 3 | ||||||
| Е1, В | Е2, В | Е3, В | R1, Ом | R2, Ом | R3, Ом | R4, Ом | |
R6=R1, R7=R2, R8=R3, R9=R4. Для всех вариантов.
Задача № 4

Рисунок 4.
В цепи рис. 4 известны значения сопротивлений резисторов R1, R2, R3, R4, R5, R6, R7, R8 и входного напряжения U. Найти токи, протекающие через каждый резистор и составить баланс мощности.
Изобразить данную схему замещения с включенными приборами: амперметром – для измерения тока в резисторе R7, вольтметром - для измерения напряжения на зажимах резистора R4 и ваттметром для измерения мощности, потребляемой резистором R5. Задачу решить методом подобия.
| Номер варианта | Данные к задаче № 4 | ||||||||
| U,В | R1,Ом | R2,Ом | R3,Ом | R4,Ом | R5,Ом | R6,Ом | R7,Ом | R8,Ом | |
| 4,0 | 1,0 | 6,0 | 2,0 | 5,0 | 8,0 | 3,0 | 6,0 | ||
| 4,0 | 2,0 | 10,0 | 3,0 | 8,0 | 6,0 | 5,0 | 10,0 | ||
| 5,0 | 3,0 | 8,0 | 1,0 | 3,0 | 8,0 | 6,0 | 8,0 | ||
| 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 2,0 | 3,0 | 4,0 | ||
| 1,0 | 3,0 | 2,0 | 4,0 | 5,0 | 6,0 | 4,0 | 2,0 | ||
| 3,0 | 2,0 | 8,0 | 2,0 | 5,0 | 4,0 | 12,0 | 12,0 | ||
| 6,0 | 3,0 | 16,0 | 5,0 | 4,0 | 8,0 | 10,0 | 16,0 | ||
| 7,0 | 2,0 | 20,0 | 3,0 | 5,0 | 10,0 | 6,0 | 20,0 | ||
| 3,0 | 2,0 | 6,0 | 5,0 | 8,0 | 4,0 | 4,0 | 6,0 | ||
| 4,0 | 3,0 | 8,0 | 1,0 | 2,0 | 6,0 | 8,0 | 8,0 |
Задача № 5
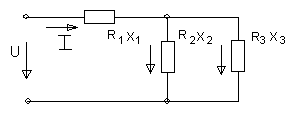 Рисунок 5.
Рисунок 5.
В цепи рис.5 активные и реактивные сопротивления соответственно равны R1,Х1; R 2,Х2; R3Х3. К зажимам цепи приложено синусоидальное напряжение, действующее значение которого равно U. Определить: а) действующие значения токов в ветвях и в неразветвленном участке; б) активную, реактивную и полную мощности в обеих ветвях и на зажимах цепи. Расчет выполнить комплексным методом. Построить векторную диаграмму.
| Номер варианта | Данные к задаче № 5 | ||||||
| U, В | R1, Ом | Х1, Ом | R2,Ом | Х2, Ом | R3, Ом | Х3,Ом | |
| -2 | |||||||
| -3 | |||||||
| -5 | |||||||
| -6 | -5 | ||||||
| -8 | |||||||
| -3 | |||||||
| -2 | |||||||
| -6 | |||||||
| -2 |
Задача № 6

Рисунок 6.
К трехфазной линии с линейным напряжением подключен симметричный трехфазный приемник, соединенный треугольником (рис.6). Активное и реактивное сопротивления фаз приемника соответственно равны по фазам. Определить ток в фазах приемника и линейных проводах, а также потребляемую приемником активную мощность в режимах: а) симметричном трехфазном, б) при обрыве одной фазы приемника; в) при обрыве линейного провода (вследствие сгорания плавкой вставки предохранителя). Построить для всех трех режимов топографические диаграммы напряжений и показать на них векторы токов.
| Номер варианта | Данные к задаче № 6 | Номер варианта | Данные к задаче №6 | |||||
| Uл, В | Rф,Ом | Хф, Ом | Uл, В | Rф, Ом | Хф,Ом | |||
| -4 | ||||||||
| -8 | ||||||||
| -15 | ||||||||
| -6 |
Задача № 7
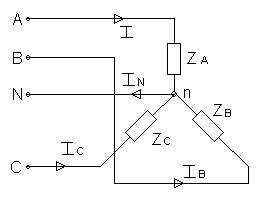
Рисунок 7.
К трехфазной линии с линейным напряжением U л подключен несимметричный приемник, соединенный по схеме «звезда» с нейтральным проводом (рис. 7). Активные и реактивные сопротивления фаз приемника
соответственно равны RА, ХА, RВ, ХВ, RСХС. Сопротивление нейтрального провода пренебрежимо мало. Определить токи в фазах приемника, линейных проводах и нейтральном проводе в режимах: а) трехфазном, б) при обрыве линейного провода А; в) при коротком замыкании фазы А приемника и обрыве нейтрального провода. Определить активную мощность, потребляемую приемником, в указанных трех режимах.
Построить для всех трех режимов топографические диаграммы напряжений и показать на них векторы токов.
| Номер варианта | Данные к задаче № 7 | ||||||
| Uл, В | RА, Ом | ХА, Ом | RВ, Ом | ХВ, Ом | RС, Ом | ХС, Ом | |
| -12 | |||||||
| -3 | |||||||
| -24 | |||||||
| -6 | |||||||
| -24 | |||||||
| -12 | |||||||
| -12 | |||||||
| -15 | |||||||
| -3 | |||||||
| -18 |
Примеры решения задач
Задача № 1

Рис.а) Рис.б)
Rвт = 1 Ом, R1 = 3 Ом, R3 = 3 Ом, R4 = 9 Ом, R5 = 6 Ом, R2 = 4,5 Ом, Е= 12 В
Преобразуем «звезду» сопротивлений R1, R2, R3 в треугольник сопротивлений RАВ, RВС, RСА по формулам
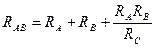 ,
,  ,
, 
Переобозначим по схеме: R1=RА, R2=RС, R3=RВ. (Такое обозначение принято в трёхфазных цепях и упрощает запоминание формул перехода Υ к Δ и наоборот).
В результате преобразования Δ вΥ получим схему б) и вычисляем RАВ=8 Ом; RВС=12 Ом; RСА=12 Ом.
Определяем Rэкв
 (1)
(1) 
Токи I4 и I5 при преобразовании схемы не изменяются.
UBC=E – IRВТ = 10 B 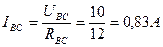
I1 = I4 + ICA = I – IBC = 2-0,83 = 1,17 A
Токи I4 и I5определим по формуле «свой – чужой»:




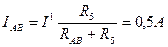
I2 = ICA + IBC = 0,5 + 0,83 = 1,33 A
I3 = IAB + IBC = 0,5 + 0,83 = 1,33 A I1 = I4 – I5 = 0 A
Если ток через сопротивление R1 не протекает, то потенциалы точек А и О равны: φА = φО. Проверим это: φА = I 4 R4 = 6 B, φO = I2R2 = 6 B.
Задача №2

R1=0,1 Ом, R2 = 0,2 Ом, R3 = 2,0 Ом, R4 = 1,0 Ом, R5 = 2,5 Ом, R6 = 1,5 Ом,
E1 = 220 B, E2 = 215 B.
По первому закону Кирхгофа 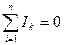 составляем У – 1 уравнение, где У – количество узлов в схеме. У = 4. Уравнения по 1- му закону Кирхгофа можно составлять для любых 3-х узлов из имеющихся 4-х.
составляем У – 1 уравнение, где У – количество узлов в схеме. У = 4. Уравнения по 1- му закону Кирхгофа можно составлять для любых 3-х узлов из имеющихся 4-х.
По II закону Кирхгофа  выбираем N = в-у+1 (в – количество ветвей в схеме) независимых контуров и составляем для каждого из них уравнение. Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую ни в какой другой контур. Для нашей схемы: N = 6–4 + 1. В каждом контуре обозначаем обход контура в произвольно выбранном направлении. В каждой ветви также в произвольном направлении обозначаем ток.
выбираем N = в-у+1 (в – количество ветвей в схеме) независимых контуров и составляем для каждого из них уравнение. Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую ни в какой другой контур. Для нашей схемы: N = 6–4 + 1. В каждом контуре обозначаем обход контура в произвольно выбранном направлении. В каждой ветви также в произвольном направлении обозначаем ток.
При составлении уравнений по 1 закону Кирхгофа произвольно условимся, что если ток втекает в узел, то в состав суммы этот ток берется со знаком «+» и наоборот.
При составлении уравнений по II закону Кирхгофа произведение Ii 
 берется со знаком «+», если направление тока в ветви совпадает с направлением обхода контура и наоборот. ЭДС входят в состав суммы с «+», если направление ЭДС совпадает с направлением обхода контура и наоборот.
берется со знаком «+», если направление тока в ветви совпадает с направлением обхода контура и наоборот. ЭДС входят в состав суммы с «+», если направление ЭДС совпадает с направлением обхода контура и наоборот.
1.  1.
1. 
2.  11.
11. 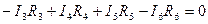
3.  111.
111. 
Таким образом, мы получили систему, состоящую из 6 уравнений с 6-ю неизвестными токами. Решаем систему методом Гаусса. Для этого составляем расширенную матрицу системы из коэффициентов, стоящих при неизвестных, т.е. из «1» и значений сопротивлений.
| 1 0 -1 -1 0 0 0 0 1 0 1 -1 0 0 -1 0 1 0 0-1 0 0,1 0 2 0 0 0 220 0 0 -2 1-2,5 -1,5 0 0-0,2 0 0-2,5 0 -215 |
Для приведения матрицы к трапецевидной форме необходимо придерживаться следующих свойств, не нарушающих равносильность системы уравнений:
1. Перемена местами строк между собой;
2. Умножение строки на любое число;
3. Прибавление к любой строке любой другой строки, предварительно умноженной на любое число.
Например, если мы к третьей строке добавим первую строку, предварительно умноженную на «1», то в результате вместо третьей строки получим такую строку:
0 0 0 – 1 0 -1 0
Если 1 строку умножить на 0,1 и сложить с 4 строкой, то новая 4-ая строка примет вид:
0 0 2,1 0,1 0 0 220
В результате в 1 столбце матрицы у нас будет «0» во всех строках, кроме первой.
Таким же образом надо добиться, чтобы во 11 столбце во всех строках, кроме 1 и 11 были «0» и т.д.
После приведения матрицы к трапецевидной форме в каждой последующей строке будет на один ноль больше, чем в предыдущей. В шестой строке должны остаться ненулевыми только два элемента: в шестом и седьмом столбцах. Теперь мы сможем найти I6, поделив элемент седьмого столбца на элемент шестого столбца. Из пятой строки мы сможем определить ток I5 и т.д. Из первой строки найдем ток I1. При наличии ПЭВМ с установленной системой Mathcad, систему уравнений можно решить с помощью функции lsolve (A,B). Для этого необходимо ввести матрицу системы А (без столбца свободных членов) и вектор свободных членов - В.
I:=lsolve (A, B).
Для нашей матрицы вектор решения имеет вид:
 |
108,3 I1 = 108,3
76,5 I2 = 76,5
I = 104,58 I 3 = 104,58
3,75 I 4 = 3,75
79,9 I 5 = 79,9
-3,75 I 6 = -3,75
Т. к. I6 <0, следовательно, истинное направление тока I6 противоположное.
Проверим баланс мощности 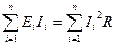 i
i
Если направление ЭДС и тока совпадают, то соответствующее слагаемое в левой части берётся со знаком «+» и наоборот. Слагаемые в правой части берутся всегда со знаком «+», т.к. значение тока входит в состав произведения в квадрате.
E1I1 + E2I2 = 
220 .108,34 + 215.76,5 = 23834,8 + 16447,5 = 40282,3 Вт
108,342 . 0,1 + 76,22 . 0,2 + 104,582. 2 +3,75 . 1 + 79,92. 2,5 + 3,752. 1,5 =
1173,7 + 1161,3 + 218 + 74 + 14 + 15960 + 21,1 = 40204,1 Вт
40282,3 ≈ 40204,1
Баланс мощностей с учетом приближенных вычислений соблюдается. Так как направления токов и ЭДС совпадают, то источники ЭДС работают в режиме генераторов.
Задача № 3
Метод узловых потенциалов
1. Принимаем потенциал одного из узлов равным нулю. Желательно выбрать нулевым потенциал такого узла, к которому подходит больше всего ветвей. Если в схеме имеется ветвь, содержащая только источник ЭДС, то необходимо «занулить» потенциал одного из узлов, примыкающих к этой ЭДС. Тогда потенциал другого узла будет известным и равным  Е (в зависимости от того, какая клемма источника ЭДС соединена с этим узлом)
Е (в зависимости от того, какая клемма источника ЭДС соединена с этим узлом)
2. Составляем уравнения для узлов с неизвестными потенциалами по очереди для каждого. Для этого в левой части уравнения пишем произведение неизвестного потенциала рассматриваемого узла, на сумму проводимостей ветвей, примыкающих к нему. Если в какой-либо из этих ветвей находится источник тока, то проводимость этой ветви не учитывается. Далее, из этого произведения вычитаем произведения потенциалов узлов, непосредственно связанных с рассматриваемым узлом схемы, на проводимости подходящих к этому узлу ветвей с учетом наличия в них источников тока. В правой части уравнения записываем алгебраическую сумму произведений ЭДС на проводимости ветвей, в которых установлены эти ЭДС. Если ЭДС подходит к узлу, произведение Eigi берется со знаком «+» и наоборот. Далее в правой части записываем алгебраическую сумму величин источников тока, находящихся в ветвях, подходящих к рассматриваемому узлу со знаком «+», если ток источника тока направлен к узлу и наоборот. При этом известные потенциалы присутствуют в уравнениях на общих правилах.
3. Решаем полученную систему линейных уравнений любым из известных методов относительно потенциалов узлов.
4. С помощью известных потенциалов узлов находим токи в ветвях по закону Ома для ветвей, содержащих ЭДС:
 (1)
(1)
Для этого в соответствии с полученными потенциалами, а следовательно, напряжением обозначаем направления токов от большего потенциала к меньшему и находим эти токи по формуле (1). Если напряжение и ЭДС совпадают по направлению, то ЭДС берется со знаком «+» и наоборот.
Для ветвей, не содержащих ЭДС 
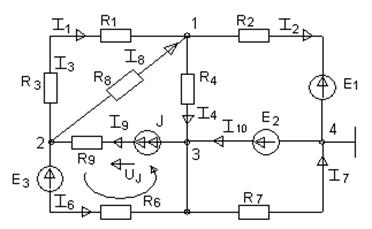
Дано: Rn =n, Ом Еn =n, B J = 1 A
Определить: Ii-?



 gi =
gi =  g1 =
g1 = 
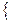 φ 1(g 1+g 2 +g 4 + g8) –φ2(g1+g8) – φ 3g 4=E 1g2
φ 1(g 1+g 2 +g 4 + g8) –φ2(g1+g8) – φ 3g 4=E 1g2
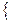 φ 2(g 1+g 6 + g8) –φ1(g1+g8) – φ 3g 6=E 3g6 +J
φ 2(g 1+g 6 + g8) –φ1(g1+g8) – φ 3g 6=E 3g6 +J
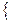 φ 1(g 1+g 2 +g 4 + g8) –φ2(g1+g8) – φ 3g 4=E 1g2 +φ 3g4
φ 1(g 1+g 2 +g 4 + g8) –φ2(g1+g8) – φ 3g 4=E 1g2 +φ 3g4
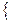 -φ1(g1+g8) + φ 2(g 1+g 6 + g8) = E 3g6 +J + φ 3g6
-φ1(g1+g8) + φ 2(g 1+g 6 + g8) = E 3g6 +J + φ 3g6
 g1 =
g1 =  См; g6 =
См; g6 = 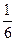 См;
См;
q2 =  См; g7 =
См; g7 =  См;
См;
q4 =  См; q8 =
См; q8 =  См
См

φ  1 = 2.62 В
1 = 2.62 В
φ2 = 5,2 В
 ;
; 
 ;
; 
 А;
А; 
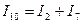
 I9 = J = 1 A
I9 = J = 1 A
Проверим баланс мощностей.
-E1I2 – E3I6 + E2I10 + UJJ = I12(R1 + R3) + I82R8 + I42R4 + I22R2 +I72R7 + I62R6+J2R9
Определим UJ.Для этого составим уравнение по 11 закону Кирхгофа для какого-либо контура, содержащего напряжение UJ.
I6R6 + JR9 = UJ – E3 UJ= I6R6 +JR9 + E3 =0,036 + 1,9 + 3 = 12,18 B


13,47 Вт = 13,470 Вт. Баланс выполняется, следовательно, все токи найдены правильно.
Задача № 4

R1= 3 Ом, R2= 2 Ом, R3=12 Ом, R4= 2 Ом, R5= 6 Ом, R6= 4 Ом, R7= 8 Ом, R8= 12 Ом, U= 110В.
Согласно методу подобия произвольно задаемся током в самой отдаленной от источника напряжения ветви. Например: I  = 1A
= 1A
 ;
;
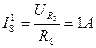 ;
;  ;
;  ;
;

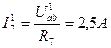




Находим коэффициент пропорциональности:
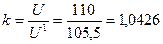
Затем, умножив все найденные токи 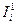 на коэффициент k, находим истинные значения токов в ветвях.
на коэффициент k, находим истинные значения токов в ветвях.
Например:
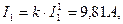 и т.д.
и т.д.
Затем находим баланс мощностей

Задача № 5

R1= 1 Ом; Х 1=0,5 Ом; R2 = 4 Ом; Х2 = -3 Ом; R3 = 8 Ом; Х3 = 6 Ом; U= 120 В; 

 ;
;  ;
; 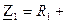 jХ1 = 1+j 0,5 Ом
jХ1 = 1+j 0,5 Ом
 jХ2 = 4 –j 3 Ом
jХ2 = 4 –j 3 Ом
 + jХ3 = 8 + j 6 Ом
+ jХ3 = 8 + j 6 Ом
Для вычисления  ЭКВ вспомним правила действия над комплексными числами.
ЭКВ вспомним правила действия над комплексными числами.
Целесообразнее производить умножение и деление комплексных чисел в показательной форме, а сложение и вычитание в алгебраической. При умножении комплексных чисел показатели их степеней складываются, а при делении – из показателя делимого вычитается показатель делителя. Модули соответственно перемножаются или делятся.
Пример 1.


Пример 2.

Для вычитания перейдем от показательной формы записи комплексного числа к алгебраической через тригонометрическую, используя формулу Эйлера.
 , где
, где
r – модуль комплексного числа, φ – его аргумент.

 ;
;
 ;
;
Переведем последнее комплексное число из алгебраической формы в показательную по формуле:


Напомним, что аргумент комплексного числа  определяется по разному в зависимости от того, в какой четверти лежит этот угол
определяется по разному в зависимости от того, в какой четверти лежит этот угол
 II I
II I
b


0 a
III IV




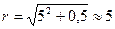
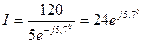 ; I=24 A
; I=24 A
Токи I1 и I2 найдем по формуле «свой-чужой».

 I1=19,3 A, I2= 9,7 A
I1=19,3 A, I2= 9,7 A

Полная мощность 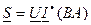 :
:
Где  - обозначается комплексно-сопряженная величина, например:
- обозначается комплексно-сопряженная величина, например:


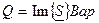

Реактивная мощность второй ветви:

 (Вар)
(Вар)

 ;
;  ;
; 
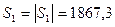 ВА, и т.д.
ВА, и т.д.
Построим векторную диаграмму токов и напряжений.
Для этого необходимо рассчитать напряжения на элементах схемы.

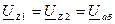
Построим векторную диаграмму
j

Uz1
I1
I2 Uаб
 0 U 120 I
0 U 120 I
Масштаб: U: 1см = 10 В; I: 1см = 0,5 А
Порядок построения векторной диаграммы токов:
1. Изображаем вектор тока  длиной (19,3
длиной (19,3  2) мм под углом 28,70.
2) мм под углом 28,70.
2. Из конца вектора  строим вектор
строим вектор  аналогичным образом.
аналогичным образом.
3. По первому закону Кирхгофа  , поэтому соединяем по правилу сложения двух векторов начало
, поэтому соединяем по правилу сложения двух векторов начало  с концом
с концом  . Получаем
. Получаем  .
.
4. Проверяем, действительно ли полученный вектор суммы  соответствует его аналитическому выражению.
соответствует его аналитическому выражению.
Векторную диаграмму напряжений строим аналогично. По второму закону Кирхгофа

Задача № 6

Дано: Uл =380 В
Rф = 15Ом
Хф = 8 Ом
Вектора линейных напряжений:


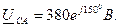
а) симметричный трёхфазный режим.
Определим ток в каждой фазе.

Поскольку цепь симметричная, остальные токи можем определить, сдвигая ток  на -1200 и – 2400.
на -1200 и – 2400.
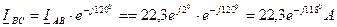

Определим линейные токи 


В силу симметричности схемы остальные линейные токи проще определить, сдвигая ток 


Определим потребляемую приёмником активную мощность
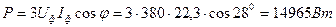
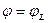
Строим топографическую диаграмму напряжений на комплексной плоскости.

I СА j U АВ
UС А
I А
I АВ
I С I В
I ВС
U ВС
б) Обрыв фазы АВ

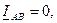 токи
токи 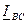 и
и  такие же как в случае а).
такие же как в случае а).


 (такой же как и в случае а)
(такой же как и в случае а)

 U СА
U СА
I СА U АВ
I С
I ВС
U ВС
в) обрыв линейного провода
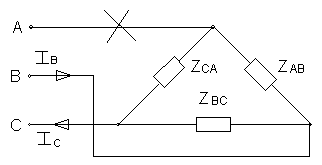



 (как в случае а))
(как в случае а))


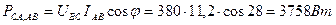
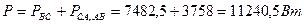
U СА U АВ

0о
I АВ
I В
U ВС
I ВС
Задача № 7

UЛ = 380 В RА=20 Ом RВ= 16 Ом RС= 12 Ом
ХА= 0 Ом ХВ=-12 Ом ХС= 9 Ом
а) Трехфазный режим
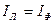 ;
; 





 ток в нейтральном проводе
ток в нейтральном проводе


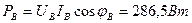


Построим топографическую диаграмму напряжений на комплексной плоскости (1,j).
 U С
U С
IN
I C
00
I А U А
I В
U В
б) Обрыв линейного провода А.

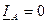
 - остаются как в режиме а); РА = 0
- остаются как в режиме а); РА = 0


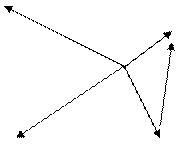 U С
U С
I N
I C
U В
I В
в) Обрыв нейтрального провода и КЗ фазы А.




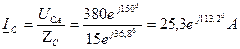

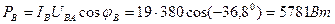


I С
U С

 n
n
А
I В
U В
Список литературы
а) основная
1. Г.И. Атабеков и др. Теоретические основы электротехники. Линейные электрические цепи. С – П.Москва. Краснодар. 2009.
2.П.А. Ионкин. Теоретические основы электротехники. Высшая школа, 1975.
3.Г.В.Зевеке и др. Основы теории цепей. Энергия, 1976.
4.М.Р. Шебес. Сборник задач и упражнений по электротехники. Высшая школа, 1992.
б) дополнительная литература
1.Ф.Е. Евдокимов. Теоретические основы электротехники. М. Академия, 2004.
2. Л.А.Бессонов. Теоретические основы электротехники. М. Академия,
2002.
Пример выполнения расчетно-графических работ с использованием программы Mathcad.











Поиск по сайту: