Порядок выполнения работы

Министерство образования и науки РФ

Профессионально-педагогический колледж

Федерального государственного бюджетного образовательного учреждения

Высшего профессионального образования

«Саратовский государственный технический университет

Имени Гагарина Ю.А.»

09.02.01 Компьютерные системы и комплексы

ОТЧЕТ

по практической работе № 2

по дисциплине «Дискретная математика»

Вычисление комбинаторных объектов заданного типа

Вариант V

Выполнил студент 2 курса

группы КСК – 922

В.А. Добров ____________

Проверил преподаватель

М.А. Ястребова _________

Работа выполнена на оценку

________________________

«___» _____________ 2015 г.

Цели работы:

1. научиться находить количество элементов в объединении нескольких множеств;

2. научиться вычислять число всевозможных комбинаторных объектов заданного типа.

Краткие теоретические сведения

Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисление элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики - алгеброй, геометрией, теорией вероятности, и имеет широкий спектр применения, например, в информатике и статистической физике.

Перестановкой n элементов множества называется их комбинация, отличающаяся только порядком расположения. В комбинаторике принято следующее обозначение: если в множестве имеется n элементов, P_n – число перестановок элементов этого множества.

Сочетаниями называются конечные подмножества, составленные из элементов данного множества. Если во множестве элементов – n, а в подмножестве m, то общее количество всех сочетаний обозначается и читается как число сочетаний из n элементов по m.

Размещениями называются конечные упорядоченные подмножества из элементов данного множества. Общее количество размещений обозначается как: и читается: число размещений из n по m (n≥m).

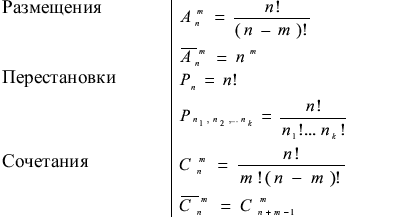
Порядок выполнения работы

Задание 1. Из 100 студентов факультета программирования 42 посещают спортивные секции, 30 — занятия научного общества, а 28 — кружки художественной самодеятельности. На занятия научного общества и спортом успевают ходить 5 студентов, спортом и художественной самодеятельностью занимаются 10, наукой и художественной самодеятельностью — 8, а сразу все три увлечения имеют три студента. Сколько студентов занимаются или в НО или художественной самодеятельностью, но не спортом?

Дано:

Всего — 100 человек

42 — посещают спортивные секции

30 — посещают занятия научного общества

28 — посещают кружки художественной самодеятельности

5 — посещают научное общество и занимаются спортом

10 — занимаются спортом и художественной самодеятельностью

8 — занимаются наукой и художественной самодеятельностью

3 — посещают спортивные секции, занятия научного общества и кружки художественной самодеятельности

Вопрос: Сколько студентов посещают или научное общество, или кружки художественной самодеятельности, но не занимаются спортом?

Решим задачу с помощью кругов Эйлера.

1) 42 + 30 + 28 - (5 + 10 + 8) + 3 = 100 - 23 + 3 = 80 — количество всех студентов,

посещающих кружки.

2) 80 – 42 = 38.

Ответ: 38 студентов посещают или научное общество, или кружки художественной самодеятельности, но не занимаются спортом.

Задание 2.

1) Из Киева до Чернигова можно добраться пароходом, поездом, автобусом и самолетом; из Чернигова до Новгорода – пароходом и автобусом. Сколькими способами можно осуществить путешествие по маршруту Киев – Чернигов – Новгород?

Дано:

А = {способы добраться из Киева в Чернигов}, n (A) = 4

B = {способы добраться из Чернигова в Новгород}, n (B) = 2

Решение:

n (A * B) = n (A) * n (B) = 4 * 2 = 8

Ответ: 8 способами.

2) В железнодорожном вагоне десять мест расположены по ходу поезда и десять – против хода поезда. Сколькими способами можно посадить в вагон восемь пассажиров, если двое отказываются сидеть лицом по ходу поезда, а трое – лицом против хода поезда?

Дано:

2 – число пассажиров, отказывающихся сидеть по ходу поезда

3 – число пассажиров, отказывающихся сидеть против хода поезда

Решение:

1)

2)

3)

4)

Ответ: 83721600 cпособов.

Задание 3. Решить уравнение: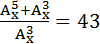

Решение:

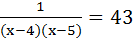
43(x – 4) (x – 5) = 0

43(x² – 5x – 4x + 20) = 0

43x² – 215x – 172x + 860 = 0

x² – 9x + 20 = 0

D = 81 – 4 *1 * 20 = 1; = 1

x₁ = = 5

x₂ = = 4

Ответ: x = 5; 4.

Выводы:

Бинарным отношением между двумя множествами называется соответствие элементов одного из них элементам второго.

Бинарные отношения встречаются не только в ма­тематике, но и всюду в жизни, вокруг нас. Родственные и другие отношения между людьми (быть отцом, дедушкой, матерью, ба­бушкой, братом, сестрой, другом, ровесником; старше, моложе, выше, ниже и др.) выступают как бинарные отношения.

Отноше­ния между событиями во времени (раньше, позже, одновременно), между предметами по их расположению в пространстве (выше, ниже, левее, правее, севернее, южнее и др.) также выступают как бинарные отношения.

Контрольные вопросы:

1. Что такое комбинаторика и для чего она нужна? Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.

2. В чем отличие сочетаний от размещений? В отличие от сочетаний размещения учитывают порядок следования предметов.

3. Запишите формулу для вычисления числа сочетаний элементов, используемую в формуле бинома Ньютона.

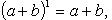
Если k -й член ((k+1)-е слагаемое) разложения степени бинома обозначать через , то

Поиск по сайту: