 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Порядок выполнения
1. Включите лазер.
Внимание! Нельзя направлять луч света лазера непосредственно
в глаз! Это может вызвать серьезную травму!
2. Расположите зеркало Ллойда «ЗЛ» на расстоянии 60–80 см от блока лазерного излучателя под углом скольжения к лазерному пучку так, чтобы пучок разделился на два (рис. 3). В направлении полученных пучков установите экран Э'.
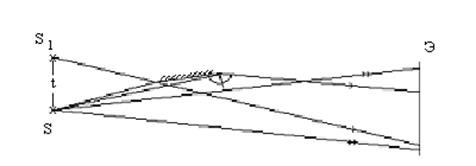
Рис. 3
3. Вращая и наклоняя зеркало, добейтесь наложения на экране Э' обоих пучков до появления интерференционной картины.
4. Полученная интерференционная картина на экране Э' очень маленькую ширину (Аl) интерференционной полосы. Для удобства измерения Dl используем рассеивающую линзу (4), для получения увеличенной интерференционной картиной уже на экране Э (рис.4).
5. Для определения увеличенной ширины интерференционной полосы, необходимо определить увеличение рассеивающей линзы. для чего измерьте расстояние «b» от рассеивающей линзы «4» до экрана Э. По формуле (9) вычислите расстояние «a».
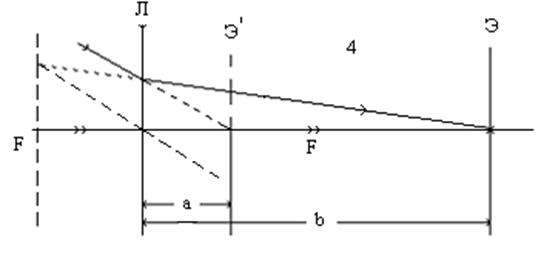
Рис. 4
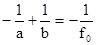 , (9)
, (9)
где а – расстояние между линзой и мнимым изображением интерференционной картиной (положение экрана Э'),
b – расстояние от линзы до экрана Э,
f0 = - 16,3 см.- фокусное расстояние рассеивающей линзы (4)
6. Рассчитайте погрешность в определении а, учтя погрешность в измерении b.
7. Из выражения
Г= 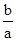 (10)
(10)
определите увеличение рассеивающей линзы 4.
8.При помощи миллиметровой линейки измерьте расстояние l между несколькими интерференционными полосами N в центре интерференционной картины. Найдите среднее значение ширины интерференционной полосы, измерения проведите для трех различных значений N интерференционных полос.
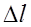 '=
'=  (12)
(12)
Чтобы уменьшить величину погрешности измерения, возьмите возможно большее число интерференционных полос N.
9.Используя выражение (10) по формуле:
Δ l′ =  (13)
(13)
10.Измерьте расстояние x от блока линз до рассеивающей линзы (4).
Найдите расстояние «L» от источника света S1 до не увеличенной интерференционной картины Э' по формуле (11).
L = f + x + a (11)
11.Определите среднее значение не увеличенной ширины интерференционной полосы.
12.Подставив формулы (9), (10), (11), (12) и (13) в (8), получим рабочую формулу
t =  (14)
(14)
по которой рассчитайте величину t.
13.Получите формулу погрешности из рабочей формулы (14)
14.Результаты измерений и вычислений внесите в таблицу.
Таблица
| № | b (см) | Δb | f (см) | а (см) | Δа | Г | L (см) | ΔL | L (мм) | N | Δl' (мм) | Δl (мм) | λ (нм) | t | Δt | 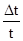 (%) (%)
|
| Ср. | 16,3 |
15.Сделайте вывод.
16.Начертите ход лучей в зеркале Ллойда.
Контрольные вопросы
1. Какие волны называются когерентными?
2. Что называют интерференцией?
3. Объясните возникновение интерференционной картины в зеркале Ллойда.
4. Запишите условия максимума и минимума при интерференции.
5. Знать вывод формулы (7) для когерентных источников.
Библиографический список:
1. Зисман Г.А. и Тодес О.М., Курс общей физики, Т.3 – М.: Наука, 1968.
2. Королев Ф.А., Курс физики. Оптика, атомная и ядерная физика.– М.: Просвещение. 1974.
3. Ландсберг Г.С., Оптика – М.: Наука 1976.
4. Сивухин Д.В. Общий курс физики. Оптика – М.: Наука 1980.
5. Иродов И.Е. Волновые процессы. Основные законы. М. – С.-П.
Приложение:
Вывод формулы интенсивности света для когерентных источников.
Интерференцией называется явление, возникающее при наложении двух (и более) волновых процессов, имеющих одинаковую частоту и выражающееся в перераспределении энергии волн в пространстве.
При наложении двух волновых процессов каждая точка становится участником двух колебаний. Результат сложения двух колебаний зависит от соотношения фаз этих колебаний.
Для световых волн большой интерес представляет сложение излучений, имеющих одинаковую частоту.
Интерференцией света называется сложение электромагнитных волн одной частоты излучения идущих от различных источников света.
При сложении волн наблюдаются два случая:
1. Сложение нескольких волн одинаковой частоты приводит просто к сложению интенсивности отдельных колебаний;
2. Имеет место более сложные явления, когда в одних местах результирующая интенсивность оказывается значительно больше суммы интенсивностей падающих излучений.
Наша задача выяснить причины такого различия в сложении нескольких световых излучений. Рассмотрим это на примере сложения двух плоско – поляризованных электро – магнитных колебаний, исходящих от двух различных источников.
Для простоты положим, что эти два колебания имеют одинаковые амплитуды.
В точке сложения колебания определяются уравнениями.

 или
или  +
+ 
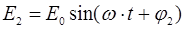 или
или 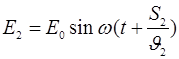
где 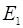 и
и 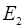 – мгновенные значения напряженности электрического поля каждой волны в данной точке,
– мгновенные значения напряженности электрического поля каждой волны в данной точке,
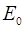 – амплитуда одинаковая для двух колебаний,
– амплитуда одинаковая для двух колебаний,
 и
и  – начальные фазы колебаний.
– начальные фазы колебаний.
Тогда, согласно принципу суперпозиции результирующая напряженность 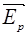 будет равна алгебраической сумме:
будет равна алгебраической сумме:
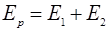
или
 (1)
(1)
С другой стороны результирующее колебание будет совершаться с амплитудой 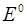 и фазой
и фазой  т.е. определяется уравнением (2):
т.е. определяется уравнением (2):
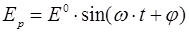 (2)
(2)
Приравниваем (1) и (2) и преобразуем эти выражения:

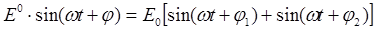
 (3)
(3)
Это равенство будет справедливо, если отдельно будут равны члены содержащие 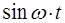 и
и 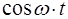 , т.е.
, т.е.
 (4).
(4).
Разделим второе на первое и получим выражение:
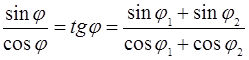 (5).
(5).
где  - начальная фаза колебаний результирующей волны.
- начальная фаза колебаний результирующей волны.
Для нахождения амплитуды результирующего колебания возведем в квадрат левые и правые части выражения (4) и сложим их:
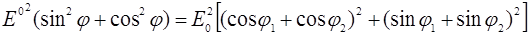
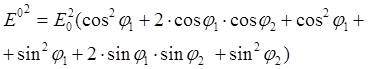
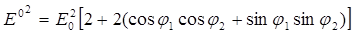
 (6).
(6).
Зная, что энергия электрического поля пропорциональна 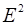 , а интенсивность света пропорциональна энергии, следовательно интенсивность света пропорциональна
, а интенсивность света пропорциональна энергии, следовательно интенсивность света пропорциональна  .
.
Учитывая это, уравнение (6) перепишется в виде:
 (7).
(7).
Если частоты колебаний в обоих волнах u - одинаковы, а разность фаз (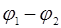 ) остается постоянной во времени, то волны называются когерентными.
) остается постоянной во времени, то волны называются когерентными.
Если 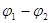
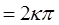 , где
, где  = 0, 1, 2…, то результирующая интенсивность имеет максимум:
= 0, 1, 2…, то результирующая интенсивность имеет максимум:
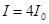
Если 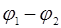
 , где
, где  = 0, 1, 2…, то результирующая интенсивность имеет минимум:
= 0, 1, 2…, то результирующая интенсивность имеет минимум:
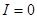 .
.
При промежуточных значениях разности фаз 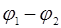 интенсивность будет принимать промежуточные значения. И график зависимости интенсивности света от х будет иметь вид (рис. 1):
интенсивность будет принимать промежуточные значения. И график зависимости интенсивности света от х будет иметь вид (рис. 1):
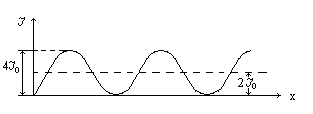
Рис. 1
Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока (энергии) в пространстве, в результате чего в одних местах возникают максимумы интенсивностей 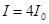 , а в других
, а в других 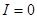 .
.
Это явление называется интерференцией световых волн.
Причем это перераспределение энергий в пространстве носит устойчивый характер во времени.
Источники света, с одинаковой частотой, у которых разность фаз не зависит от времени и которые дают устойчивую во времени интерференцию света, называются когерентными.
Если источники не связаны друг с другом и колеблются независимо, то разность фаз 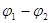 имеет различные случайные значения от 0 до
имеет различные случайные значения от 0 до 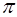 , а
, а 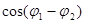 имеют с равной вероятностью как положительные, так и отрицательные значения (от +1 до –1) и тогда
имеют с равной вероятностью как положительные, так и отрицательные значения (от +1 до –1) и тогда 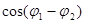 в среднем по времени будет равен 0. Результирующая интенсивность от двух источников света при этом будет равна сумме интенсивностей:
в среднем по времени будет равен 0. Результирующая интенсивность от двух источников света при этом будет равна сумме интенсивностей:
 .
.
т.е. для таких световых волн интенсивность результирующего колебания не будут меняться, т.е. перераспределение энергии в пространстве происходить не будет. Источники называют некогерентными. Интерференционная картина не наблюдается.
Из опыта известно, что любые два независимых источника не дают интерференционной картины, а освещенность поверхности монотонно убывает по мере удаления от источника. Это объясняется тем, что естественные источники света не когерентны.
Излучение светящегося тела складывается из волн, испускаемых возбужденными атомами. Излучение отдельного атома продолжается около 10-8с. За это время успевает образоваться последовательность горбов и впадин (или как говорят, цуг волн).
«Погаснув» атом через некоторое время «вспыхивает» вновь. Однако фаза нового цуга волн никак не связана с фазой предыдущего цуга. Одновременно «вспыхивает» большое количество атомов. Возбуждаемые ими цуги волн, налагаясь друг на друга, образуют испускаемую телом световую волну. В чистой волне излучение одной группы атомов через время порядка 10-8с сменяется излучением другой группы, причем фаза результирующей волны претерпевает случайные скачкообразные изменения.
Когерентные световые волны можно получить, разделив (с помощью отражения и преломления) волну, излучаемую одним источником, на две части. Если эти две волны заставить пройти разные оптические пути, а потом наложить их друг на друга, наблюдается интерференционная картина.
Поиск по сайту: