Практическое занятие. Тема. Геометрические векторы

Тема. Геометрические векторы. Операции над векторами. Базис и координаты вектора.

Тема. Длина и направляющие косинусы вектора. Координаты точки. Расстояние между точками. Деление отрезка в данном отношении.

2.4 В треугольнике дано , , 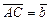точка - середина стороны . Выразить вектор через векторы и .

2.5 В треугольнике : - точка пересечения медиан треугольника, и 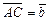. Разложить и по векторам и .

2.6 Векторы , служат диагоналями параллелограмма . Выразить векторы через векторы и .

2.7 В треугольнике сторона точками и разделена на три равные части . Выразить вектор через векторы и , если .

2.8 В треугольнике проведены медианы . Представить векторы через векторы и . Найти сумму векторов .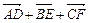

2.9 В треугольнике : и , где , . Полагая и , выразить и через векторы и .

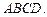2.11 Точки и служат серединами сторон и четырехугольника Доказать, что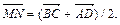

2.12 Дан тетраэдр Выразить через векторы вектор началом которого служит середина E ребра OA, а концом - середина F ребра BC.

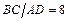2.17 В трапеции отношение оснований . Принимая за базис векторы 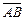и найти координаты векторов

2.18 Вне плоскости параллелограмма взята точка В базисе из векторов найти координаты:

а) вектора где -точка пересечения диагоналей параллелограмма; б) вектора где - середина стороны

2.19 Дан тетраэдр . В базисе из рёбер , и найти координаты вектора , где - точка пересечения медиан основания .

2.20 В трапеции отношение оснований 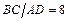. Принимая за базис векторы найти координаты векторов

2.27 Заданы векторы , , .

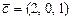Найти: а) и координаты орта ; б) координаты вектора .

2.28 Заданы векторы , , .

Найти: а) и координаты орта ; б) координаты вектора .

2.29 Найти длину и направляющие косинусы вектора если .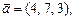

2.30 Определить координаты вектора , если известно, что он направлен в противоположную сторону к вектору , и его модуль равен 5.

2.31 Найти вектор , коллинеарный вектору , образующий с ортом острый угол и имеющий длину .

2.32 Найти координаты вектора , длина которого равна 8, зная, что он образует с осью Ox угол , с осью Oz - угол , а с осью Oy - острый угол.

2.33 Найти вектор , образующий с ортом угол 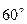, с ортом - угол , если .

2.34 Найти вектор , образующий со всеми тремя базисными ортами равные острые углы, если .

2.35 Определить расстояние между двумя точками:

а) и ; и ;

б) и ; и .

2.36. Определить ординату точки , зная, что абсцисса ее равна , а расстояние до точки равно .

2.37 На оси ординат найти точку, отстоящую от точки на расстояние 5 единиц.

2.38 На оси абсцисс найти точку, равноудаленную от начала координат и точки

2.39 На оси Oz найти точку, равноудаленную от точек: 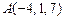и

2.40 Один из концов отрезка находится в точке А (2,3), его серединой служит точка . Найти другой конец отрезка.

2.41. Найти вершины треугольника , зная середины его сторон: ,

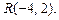
2.42 Даны середины сторон треугольника Найти координаты его вершин.

2.43 Вычислить длину медиан треугольника, зная координаты его вершин:

2.44 Даны две точки и . В каком отношении делит отрезок точка С пересечения отрезка АВ с биссектрисой первого и третьего координатных углов?

2.45 Даны две смежные вершины параллелограмма ABCD: и В( 2,6) и точка пересечения его диагоналей М (3,1). Найти две другие вершины параллелограмма.

Ответы:

2.4 . 2.5 .

2.6 . 2.7 .

2.8 , .

2.9 , 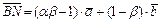. 2.12 .

2.17 . 2.18 .

2.19 . 2.20 .

2.21. 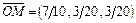. 2.22. . 2.23. а) ; б) ; в) . 2.24.а) компланарны; б) не компланарны; в) компланарны.

2.25. ; 2.26. . 2.27. а) , ; б) .

2.28. а) , ; б) .

2.29 . 2.30 . 2.31 . 2.32 . 2.33 . 2.34 .

2.35 а) ; б) . 2.36 . 2.37 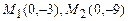. 2.38 . 2.39 . 2.40 . 2.41 . 2.42 . 2.43 . 2.44 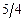2.45 .

2.46 . 2.47 .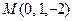

Поиск по сайту: