 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Практическое занятие
Тема. N – мерный арифметический вектор. Линейные операции над векторами (сложение, умножение на число, линейная комбинация векторов). Линейная зависимость и независимость систем векторов. Ранг и базис системы векторов, пространства  . Представление вектора в данном базисе
. Представление вектора в данном базисе  , координаты вектора. Скалярное произведение, ортогональность векторов.
, координаты вектора. Скалярное произведение, ортогональность векторов.
Арифметическим вектором называется всякая упорядоченная совокупность из  чисел:
чисел: 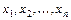 и обозначается
и обозначается  . Числа
. Числа  называются компонентами вектора
называются компонентами вектора  , число компонент называется его размерностью. Векторы
, число компонент называется его размерностью. Векторы  и
и  называются равными, если они одной размерности и их соответствующие элементы равны:
называются равными, если они одной размерности и их соответствующие элементы равны:  ,
,  . Суммой (разностью) векторов
. Суммой (разностью) векторов  и
и  одной размерности, называется вектор
одной размерности, называется вектор  той же размерности, для которого:
той же размерности, для которого:  ,
,  . Произведением вектора
. Произведением вектора  на число
на число  называется вектор
называется вектор  той же размерности, для которого:
той же размерности, для которого:  ,
,  . Линейной комбинацией векторов
. Линейной комбинацией векторов  и
и  одной размерности, называется вектор
одной размерности, называется вектор  той же размерности (
той же размерности ( и
и  - произвольные числа), для которого:
- произвольные числа), для которого:  ,
,  . Скалярным произведением векторов
. Скалярным произведением векторов  и
и  называется число, определяемое формулой:
называется число, определяемое формулой:  . Два вектора
. Два вектора  и
и  называются ортогональными, если
называются ортогональными, если  .
.
Множество всех  -мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называется пространством арифметических векторов (векторным пространством) и обозначается
-мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называется пространством арифметических векторов (векторным пространством) и обозначается  . Система векторов
. Система векторов  называется линейно зависимой, если найдутся числа
называется линейно зависимой, если найдутся числа  , не равные одновременно нулю, такие, что
, не равные одновременно нулю, такие, что  (где
(где 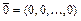 - нулевой вектор). Если равенство выполняется, только при
- нулевой вектор). Если равенство выполняется, только при  , то система называется линейно независимой. Базисом системы векторов
, то система называется линейно независимой. Базисом системы векторов  называется упорядоченная система векторов
называется упорядоченная система векторов  , удовлетворяющая условиям: 1)
, удовлетворяющая условиям: 1)  ,
,  ; 2) система
; 2) система  линейно независима; 3) для любого вектора
линейно независима; 3) для любого вектора 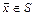 найдутся числа
найдутся числа  , такие, что
, такие, что  . Коэффициенты
. Коэффициенты  , однозначно определяемые вектором
, однозначно определяемые вектором  , называются координатами вектора в базисе
, называются координатами вектора в базисе  , а формула называется разложением вектора
, а формула называется разложением вектора  по базису
по базису  . Рангом системы векторов
. Рангом системы векторов  называется число векторов в любом из её базисов и обозначается
называется число векторов в любом из её базисов и обозначается  или
или  . В пространстве
. В пространстве  базисом является всякая упорядоченная система из
базисом является всякая упорядоченная система из  линейно независимых векторов:
линейно независимых векторов:  . Ранг пространства
. Ранг пространства  равен
равен  и называется его размерностью. Координаты одного и того же вектора
и называется его размерностью. Координаты одного и того же вектора  в двух базисах
в двух базисах 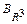 и
и  связаны соотношением:
связаны соотношением:  , где матрица
, где матрица  , столбцами которой являются коэффициенты
, столбцами которой являются коэффициенты  разложения векторов
разложения векторов  по базису
по базису  :
:  ,
,  , называется матрицей перехода от базиса
, называется матрицей перехода от базиса 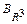 к базису
к базису  . Понятие ранга матрицы используется для исследования линейной зависимости системы векторов и нахождения её ранга. Ранг системы векторов равен рангу матрицы, столбцами которой являются координатные столбцы векторов системы. Система векторов будет линейно зависима, если её ранг меньше числа векторов в системе.
. Понятие ранга матрицы используется для исследования линейной зависимости системы векторов и нахождения её ранга. Ранг системы векторов равен рангу матрицы, столбцами которой являются координатные столбцы векторов системы. Система векторов будет линейно зависима, если её ранг меньше числа векторов в системе.
В задачах 1.59-1.60 найти линейные комбинации векторов, если заданы арифметические векторы:  ,
, 
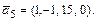
1.59 а)  ; б)
; б)  . 1.60 а)
. 1.60 а)  ; б)
; б)  .
.
В задачах 1.61-1.62 найти вектор  из уравнений.
из уравнений.
1.61  , где
, где  ,
,  ,
,  .
.
1.62  , где
, где  ,
,  ,
,  .
.
В задачах 1.63-1.68 выяснить, являются ли следующие системы арифметических векторов линейно зависимыми или линейно независимыми.
1.63  ,
,  . 1.64
. 1.64  ,
,  .
.
1.65  ,
,  ,
,  . 1.66
. 1.66  ,
,  ,
,  .
.
1.67  ,
,  ,
,  ,
,  .
.
1.68  ,
,  ,
,  ,
,  .
.
1.70 Представить вектор  как линейную комбинацию векторов
как линейную комбинацию векторов 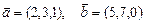 и
и  :
:
а)  ; б)
; б)  ; в)
; в)  .
.
1.71 Найти все значения  при которых вектор
при которых вектор  линейно выражается через векторы
линейно выражается через векторы  :
:
а)  ,
,  ,
,  ,
,  ; б)
; б)  ,
, 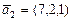 ,
,  ,
,  ;
;
в)  ,
,  ,
,  ,
,  ; г)
; г)  ,
,  ,
,  ,
,  .
.
1.73 Найти какой-нибудь базис системы векторов и выразить через этот базис остальные векторы системы:
а)  ,
,  ,
,  ;
;
б) 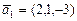 ,
,  ,
,  ,
,  .
.
1.74 Показать, что векторы 
 образует базис в
образует базис в  и вычислить координаты вектора
и вычислить координаты вектора  в этом базисе.
в этом базисе.
1.75 Найти координаты вектора  в базисе
в базисе 
 :
:
а)  ,
,  ,
,  ,
,  ; б)
; б)  ,
, 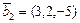 ,
,  ,
,  ;
; 
в)  ,
,  ,
,  ,
,  ,
,  ;
;
г)  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
1.76 Найти координаты вектора  в базисе
в базисе  , если он задан в базисе
, если он задан в базисе  :
:
а)  , б)
, б)  , в)
, в)  , г)
, г)  ,
,
 ;
;  ;
;  ;
;  .
.
В задачах 1.88-1.90 найти ранг системы векторов
1.88  ,
,  ,
,  ,
,  ,
,  .
.
1.89  ,
,  ,
,  ,
,  .
.
1.90  ,
, 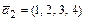 ,
,  .
.
1.123.1 Вычислить скалярное произведение векторов и выяснить будут ли они ортогональными.
а) 
 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Ответы.
1.59 а) (1,4,-7,7); б) (4,6,-35,-1) 1.60 а) (70,40,-20,-16); б) (51,26,37/2,-23/2)
1.61  1.62
1.62 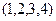 1.63 Независима. 1.64 Зависима. 1.65 Независима. 1.66 Зависима. 1.67. Независима. 1.68 Зависима. 1.70 а)
1.63 Независима. 1.64 Зависима. 1.65 Независима. 1.66 Зависима. 1.67. Независима. 1.68 Зависима. 1.70 а)  ; б)
; б)  ; в)
; в)  . 1.71 а)
. 1.71 а)  ; б)
; б)  -любое число; в)
-любое число; в)  ; г) такого
; г) такого  не существует. 1.73 а)
не существует. 1.73 а)  ; б)
; б)  . 1.74
. 1.74  1.75а)
1.75а)  ; б)
; б)  ; в)
; в)  ;г)
;г)  1.76 а)
1.76 а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  . 1.88 3 1.89 3 1.90 2 1.123.1 а)
. 1.88 3 1.89 3 1.90 2 1.123.1 а)  , да; б)
, да; б)  , нет; в)
, нет; в)  , нет; г)
, нет; г)  , да.
, да.
Поиск по сайту: