АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

б) Построим графики исходной, линейной и квадратичной зависимостей

Читайте также:
  1. II. Элементы линейной и векторной алгебры.
  2. Алгоритм оценки и проверки адекватности нелинейной по параметрам модели (на примере функции Кобба-Дугласа).
  3. Аппроксимационная задача линейной регрессии
  4. ВИДЫ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
  5. Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении
  6. Графики Никурадзе и Мурина
  7. Диаграммы и графики
  8. Задание №2. Построение и анализ линейной линии тренда
  9. Индексе цен) в парной линейной регрессии? (короткая и развернутая форма
  10. Какое предположение о матрице факторов Х не является предпосылкой классической линейной регрессионной модели.
  11. Классическая и обобщенная модели множественной линейной регрессии. Условия применения метода наименьших квадратов, свойства его оценок.

Лабораторная работа №10

Использование численных методов для решения задач

А) Найти параметры линейной и квадратичной зависимости методом наименьших квадратов

Б) Построить графики исходной, линейной и квадратичной зависимостей

В) Оценить погрешность найденных зависимостей

  Зависимость  
  хi 0,6 0,9 1,4 1,5 4,5  
уi          
               

Решение:

а) Найдём параметры линейной и квадратичной зависимости методом наименьших квадратов

Будем искать линейную зависимость в виде: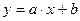

Определить параметры линейной зависимости можно, решив систему линейных уравнений:

 

Для написания формул используем редактор формул.

Для этого построим таблицу и найдём соответствующие суммы:

 

  хi уi хi×уi хi2
  0,6   3,6 0,36
  0,9   7,2 0,81
  1,4   9,8 1,96
  1,5   7,5 2,25
  4,5   40,5 20,25
å 8,9   68,6 25,63

 

Составим систему линейных уравнений и, решив её, найдём параметры линейной зависимости:

Воспользуемся формулами Крамера или используем функцию МОПРЕД:

 

∆= 25,63 8,9 = 48,94
8,9  
         
∆a= 68,6 8,9 = 31,5
   
         
∆b= 25,63 68,6 = 286,51
8,9  

 

а= 31,5 = 0,643645
48,94
       
b= 286,51 = 5,854311
48,94

 

Полученная линейная зависимость:

 

Будем искать квадратичную зависимость в виде:

Определить параметры квадратичной зависимости можно, решив систему линейных уравнений:

Для этого построим таблицу и найдём соответствующие суммы:

 

  хi уi хi×уi хi2 хi3 хi4 хi2×уi
  0,6   3,6 0,36 0,216 0,1296 2,16
  0,9   7,2 0,81 0,729 0,6561 6,48
  1,4   9,8 1,96 2,744 3,8416 13,72
  1,5   7,5 2,25 3,375 5,0625 11,25
  4,5   40,5 20,25 91,125 410,0625 182,25
å 8,9   68,6 25,63 98,189 419,7523 215,86

 

Составим систему линейных уравнений и, решив её, найдём параметры квадратичной зависимости:

Воспользуемся формулами Крамера или функцией МОПРЕД:

 

  419,7523 98,189 25,63    
∆= 98,189 25,63 8,9 = 296,2079
  25,63 8,9      
           
  215,86 98,189 25,63    
∆a= 68,6 25,63 8,9 = 127,9836
    8,9      
           
  419,7523 215,86 25,63    
∆b= 98,189 68,6 8,9 = -496,698
  25,63        
           
  419,7523 98,189 215,86    
∆b= 98,189 25,63 68,6 = 2301,534
  25,63 8,9      

 

a= 127,9836 = 0,432074
296,2079
       
b= -496,698 = -1,67686
296,2079
       
c= 2301,534 = 7,769996
296,2079

 

Полученная квадратичная зависимость:

 

б) Построим графики исходной, линейной и квадратичной зависимостей

 

Для этого найдём значения функции по приближённым формулам линейной и квадратичной зависимостей, результат оформим в виде таблицы:

 

  хi уi уприбл.лин. уприбл.квадр.
  0,6   6,240499 6,919428
  0,9   6,433592 6,610804
  1,4   6,755415 6,26926
  1,5   6,819779 6,226876
  4,5   8,750715 8,973631

 

Построим графики функций:

 

в) Оценим погрешность найденных зависимостей по формуле:

 
 

 


Линейная зависимость

 

  хi уi уприбл (уi-уприбл)2
  0,6   6,240499 0,05784
  0,9   6,433592 2,453634
  1,4   6,755415 0,059822
  1,5   6,819779 3,311597
  4,5   8,750715 0,062143
å 8,9     5,945035

 

Погрешность 2,438244

 

Квадратичная зависимость

 

  хi уi уприбл (уi-уприбл)2
  0,6   6,919428 0,845348
  0,9   6,610804 1,929865
  1,4   6,26926 0,53398
  1,5   6,226876 1,505225
  4,5   8,973631 0,000695
å 8,9     4,815114

 

Погрешность 2,194337

 

Вывод: При нахождении значения функции использование эмпирической функции квадратичной зависимости даёт меньшую погрешность, чем использование эмпирической функции линейной зависимости.

 


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)