 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
II. Элементы линейной и векторной алгебры
ФОРМУЛИРОВКА ЗАДАНИЯ И ЕГО ОБЪЕМ
Контрольная работа по дисциплине «Математика» является одной из форм самостоятельной работы студента.
Цель контрольной работы – углубить или закрепить практические знания студентов по избранным вопросам вычисления пределов, нахождения производных функций и исследования функций.
Контрольная работа №1 состоит из десяти заданий и выполняется по вариантам.
Контрольная работа №2 состоит из шести заданий и выполняется по вариантам.
1.1. Выбор вариантов контрольной работы
Вариант контрольной работы соответствует последней цифре номера зачетной книжки. Выбор варианта должен осуществляться строго в соответствии с этим правилом, в противном случае работа считается незачтенной и возвращается студенту на переработку.
КОНТРОЛЬНАЯ РАБОТА №1
Задание контрольной работы
I. Аналитическая геометрия.
Задание №1. Составить каноническое уравнение: а) эллипса; б) гиперболы; в) параболы (А, В – точки, лежащие на кривой, F – фокус, a – большая (действительная) полуось, b – малая (мнимая) полуось, 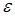 – эксцентриситет,
– эксцентриситет, 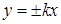 – уравнения асимптот гиперболы, D – директриса кривой, 2с – фокусное расстояние).
– уравнения асимптот гиперболы, D – директриса кривой, 2с – фокусное расстояние).
5. а) 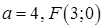 ; б)
; б)  ; в)
; в) 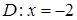 .
.
Задание №2. Даны векторы 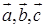 . Необходимо: а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов; г) проверить, будут ли коллинеарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора.
. Необходимо: а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов; г) проверить, будут ли коллинеарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора.
5. 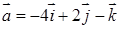 ,
, 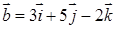 ,
, 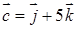 ;
;
а) 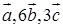 ; б)
; б) 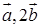 ; в)
; в)  ; г)
; г)  ; д)
; д) 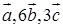 .
.
II. Элементы линейной и векторной алгебры.
Задание №1. Вычислить определители третьего порядка. При вычислении применить: а) метод треугольников; б) теорему Лапласа, разлагая по любой строке или столбцу:
| 1. | 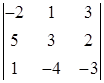 , ,
| 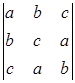 ; ;
| 2. | 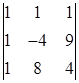 , ,
| 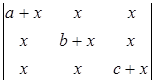 ; ;
|
| 3. | 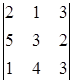 , ,
| 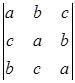 ; ;
| 4. | 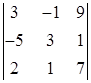 , ,
| 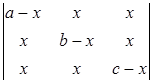 ; ;
|
| 5. | 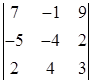 , ,
|  ; ;
| 6. |  , ,
| 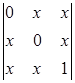 ; ;
|
| 7. |  , ,
|  ; ;
| 8. | 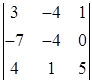 , ,
| 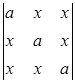 ; ;
|
| 9. | 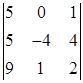 , ,
| 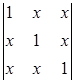 ; ;
| 10. | 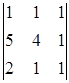 , ,
| 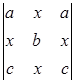 ; ;
|
Задание №2. Пусть даны три матрицы: 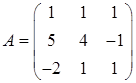 ,
, 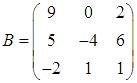 ,
, 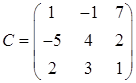 . Вычислить выражение:
. Вычислить выражение:
5. 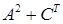 ; ;
|
Задание №3. Доказать совместность системы и решить ее тремя методами: а) методом Гаусса, б) методом Крамера, в) матричным методом:
Поиск по сайту: