 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Скорость точки в данный момент времени
Кинематика
Кинематика -это раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (т.е. массы) и действующих на них сил.
Для определения положения движущегося тела (или точки) с тем телом, по отношению к которому изучается движение данного тела, жестко, связывают какую-нибудь систему координат, которая вместе с телом образует систему отсчета.
Основная задача кинематики состоит в том, чтобы, зная закон движения данного тела (точки), определить все кинематические величины, характеризующие его движение (скорость и ускорение).
Способы задания движения точки
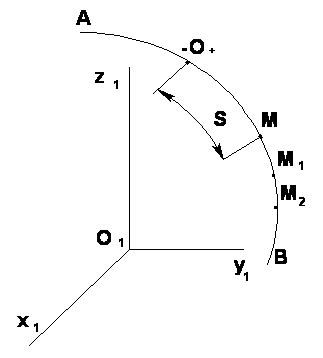
· Естественный способ
Должно быть известно:
-- траектория движения точки;
-- начало и направление отсчета;
-- закон движения точки по заданной траектории в форме (1.1)
|
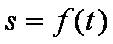 (1.1) (1.1)
|
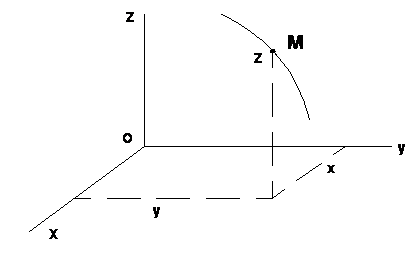
· Координатный способ
| 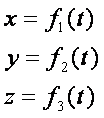 (1.2) (1.2)
|
Уравнения (1.2) – уравнения движения точки М.
Уравнение траектории точки М можно получить, исключив параметр времени «t» из уравнений (1.2)
· Векторный способ
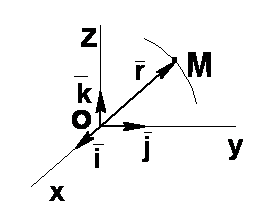
| 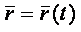 (1.3)
Связь между координатным и векторным способами задания движения точки (1.3)
Связь между координатным и векторным способами задания движения точки
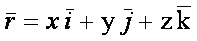 (1.4) (1.4)
|
Связь между координатным и естественным способами задания движения точки
-- определить траекторию точки, исключив время из уравнений (1.2);
-- найти закон движения точки по траектории (воспользоваться выражением для дифференциала дуги)
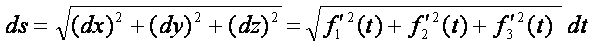
После интегрирования получим закон движения точки по заданной траектории:
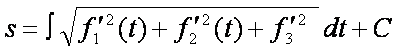
Связь между координатным и векторным способами задания движения точки определяется уравнением (1.4)
Определение скорости точки при векторном способе задания движения.
Пусть в момент времени t положение точки определяется радиусом-вектором 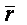 , а в момент времени t1 – радиусом-вектором
, а в момент времени t1 – радиусом-вектором 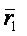 , тогда за промежуток времени
, тогда за промежуток времени 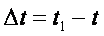 точка совершит перемещение
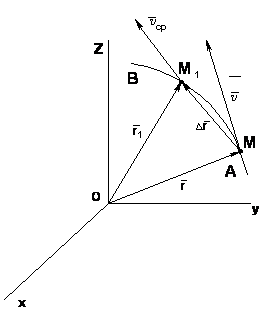
точка совершит перемещение 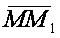 .
.
| 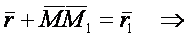
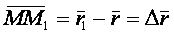
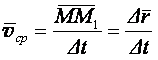 (1.5)
средняя скорость точки,
направлен вектор также как и вектор (1.5)
средняя скорость точки,
направлен вектор также как и вектор
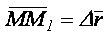
|
Скорость точки в данный момент времени
Чтобы получить скорость точки в данный момент времени, необходимо совершить предельный переход
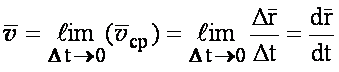 (1.6)
(1.6)
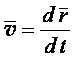 (1.7)
(1.7)
Вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора по времени и направлен по касательной к траектории в данной точке.
(единица измерения ¾ м/с, км/час)
Поиск по сайту: