Ускорение точки при векторном способе задания движения

(1.8)   (1.9)   (1.10)

Вектор среднего ускорения имеет то же направление, что и вектор Δ v, то есть, направлен в сторону вогнутости траектории.

Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

(еденица измерения - )

Как располагается вектор по отношению к траектории точки?

При прямолинейном движении вектор направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения , также как и вектор _ср лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор _ср будет направлен в сторону вогнутости траектории и будет лежать в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке М₁. В пределе, когда точка М₁ стремится к М эта плоскость занимает положение так называемой соприкасающейся плоскости. Следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Определение скорости и ускорения точки при координатном способе задания движения

ТЕОРЕМА: Проекция производной от вектора на какую-нибудь неподвижную ось равна производной от проекции вектора на ту же ось.

.

(2.1)

(2.2)

Если

то (2.3)

Определение скорости точки

Так как, и

но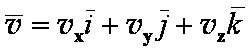

На основании (1.13), получим

(2.4)

или

Таким образом, проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени.

(2.5)

Система (1.15) определяет модуль и направление вектора скорости точки в пространстве. 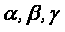- углы, которые образует вектор скорости точки с осями координат.

Определение ускорения точки

(2.6)

Следовательно

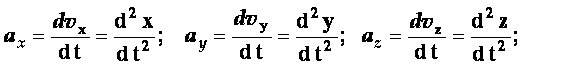(2.7)

или

Таким образом, проекции ускорения на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени.

Поиск по сайту: