ИГРЫ С ПРИРОДОЙ

Игры с природой относятся к задачам теории статистических решений. Человек или автомат, принимающий решение, не располагает полной информацией о всех фактах, влияющих на выбор этого решения, т.е. действует в условиях полной неопределенности, в условиях риска. Однако в ряде задач может быть известно распределение вероятностей поведения «природы». Решение принимается на основе некоторых критериев, каждый из которых учитывает или распределение вероятностей и средний выигрыш, или максимальный выигрыш, или риск.

Рассмотрим некоторые из этих критериев.

Пусть игра задана матрицей 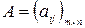. Строкам i этой матрицы соответствуют действия, стратегии человека. Столбцам j – состояние природы. Матрица А – матрица выигрышей (дохода, прибыли), – выигрыш человека при выборе i -й стратегии и при состоянии природы j.

1. Вероятностный критерий.

Если известно распределение , вероятностей состояний природы, то действия, выбор стратегий поведения, направлены на получение максимальной средней прибыли: , .

Пример 7

Найти решение игры, заданной матрицей , если известно распределение вероятностей состояний природы (0,1; 0,4; 0,5).

Решение

Сведем данные в таблицу и вычислим по строкам математические ожидания выигрыша с учетом всех состояний природы.

.

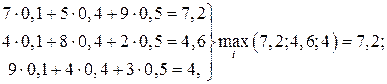
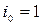Выбираем стратегию 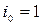, средний выигрыш m = 7,2.

2. Критерий Лапласа

Если вероятности состояний природы неизвестны, то можно предположить, что все состояния равновероятны, то 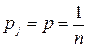, 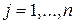. Максимальный средний выигрыш , .

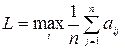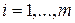Пример 8

Найти решение игры, заданной матрицей , если все состояния природы равновозможны.

Решение

Применим критерий Лапласа. Максимуму 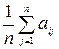соответствует максимум , .

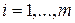Вычислим суммы элементов каждой строки и по max выберем стратегию .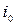

, .

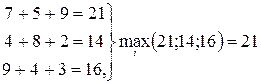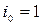Выбираем стратегию 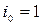, средний выигрыш .

3. Максиминный критерий Вальда

Если ничего не известно о вероятностях соотношений природы, то выбираем ту стратегию 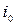, при которой

, ; .

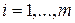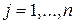Пример 9

Найти решение игры, заданной матрицей .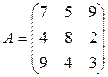

Решение

В матрице А найдем по строкам 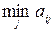и выберем из этих чисел максимальное.

, .

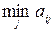
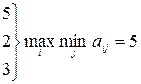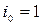Выбираем стратегию 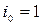, максимальный из минимальных выигрышей W =5.

4. Критерий Севиджа

Критерий Севиджа называют также критерием минимального риска.

Риском 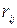называется разность , где , ; .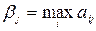

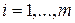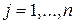Матрицей 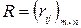– матрица рисков.

По строкам этой матрицы выбираем стратегию, обеспечивающую минимальный риск из максимальных.

.

Пример 10

Найти решение игры, заданной матрицей .

Решение

Применим критерий Севиджа. В каждом столбце матрицы А найдем 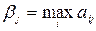, i = 1,2,3 и запишем матрицу рисков R.

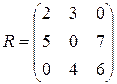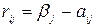, , , i = 1,2,3.

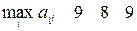
В каждой строке матрицы R выберем 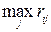и найдем наименьший из

максимальных рисков.

, .

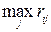
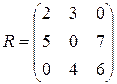
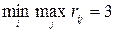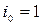Выбираем стратегию 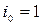, минимальный из максимальных рисков S =3.

5. Критерий Гурвица

Критерий Гурвица основан на коэффициенте доверия – экспертной оценке 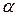, 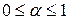. Решение принимается согласно

.

При получим критерий Вальда.

Пример 11

Найти решение игры, заданной матрицей при .

Решение

Умножим наименьший в строке элемент на , а наибольший – на 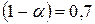и вычислим суммы этих произведений для каждой строки. Среди этих сумм найдем максимальную:

; .

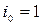Выбираем стратегию 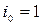, G = 7,8.

Замечание

Разные критерии могут приводить к различным решениям задачи.

Пример 12

Экономисты оптово-торгового предприятия на основе возможных вариантов поведения поставщиков 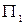, , 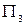разработали несколько хозяйственных планов 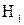, , , , 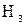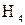. Результаты всех возможных исходов приведе-

ны в таблице.

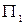
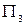
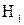
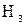
Определить оптимальный план торгового предприятия, если вероятности
исходов заданы матрицей .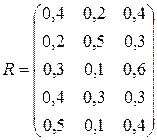

Решение

1 Применим вероятностный критерий 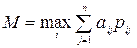, 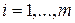. Сведем данные в одну таблицу и вычислим математические ожидания по строкам, из них выберем максимальное: .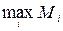

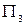
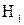
	0,4	0,2	0,4
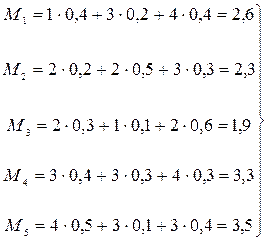
	0,2	0,5	0,3
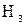
	0,3	0,1	0,6	; .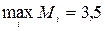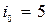
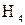
	0,4	0,3	0,3
	0,5	0,1	0,4

Выбираем план .

2 Применим критерий Вальда

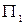
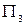
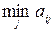
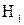
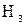
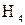
Выбираем один из двух планов , .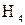

3 Применим критерий Севиджа .

R

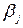
Выбираем один из двух планов , .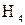

4 Применим критерий Гурвица при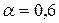

, .

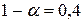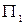
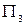
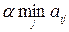
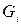
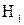
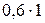
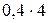
						2,2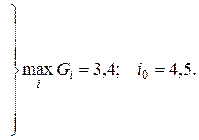
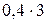
						2,4
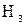
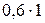
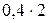
						1,4
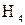
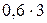
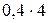
						3,4
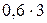
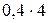
						3,4

Выбираем один из двух планов , .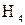

Задание 5

Задача 1

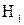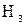Возможно строительство 4-х типов электростанций – тепловых, – приплотинных, – бесшлюзовых, 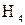– шлюзовых. Эффективность каждой из них зависит от различных факторов (режим рек, стоимость топлива и т.п.). Предполагается, что выделено 3 различных состояния 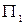, , , 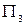каждое из которых означает определенное сочетание факторов, влияющих на эффективность электростанций. Экономическая эффективность электростанций зависит от состояний природы и задана матрицей А. Требуется принять решение о строительстве электростанции одного из 4-х типов.

1 Применить критерий Лапласа, полагая .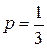

2 Применить критерий Вальда.

3 Применить критерий Севиджа.

4 Применить критерий Гурвица при .

Задача 2

На технологическую линию может поступать сырье разного качества. Известно, что в 60 % случаев поступает сырье с малым количеством примесей 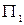, в 30 % случаев поступает сырье с допустимым количеством примесей и в 10 % случаев поступает сырье с большим количеством примесей 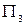. На технологической линии предусмотрены 3 режима работы 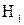, , 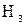. Прибыль предприятия от реализации продукции, производимой этой линией, зависит от качества сырья 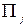, j = 1,2,3 и от режима работы 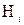, I = 1,2,3. Эта прибыль в расчете на один день приведена в матрице А. Определить, какой из режимов работы обеспечит максимальную прибыль.

Поиск по сайту: