АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

РЕШЕНИЕ ИГРЫ В СМЕШАННЫХ СТРАТЕГИЯХ

Читайте также:
  1. VI. ЭТАП Определения лица (группы лиц) принимающих решение.
  2. А если и может, то Конституционный суд отменит это решение в пять минут.
  3. Альтернативное разрешение споров
  4. В заданиях 10-14 запишите ответ в отведенном для этого поле. Для заданий 11,12,13 запишите полное решение.
  5. В заданиях 10-14 запишите ответ в отведенном для этого поле. Для заданий 11,12,13 запишите полное решение.
  6. Влияние на решение о покупке
  7. Возможное решение
  8. Возможное решение
  9. Возможное решение проблемы ограниченности ресурсов и благ
  10. Геометрическое решение биматричных игр 2x2.
  11. Глава 7. Гениальное решение
  12. Глава II. Решение системы линейных уравнений с использованием компьютерных приложений

Если игра не имеет Седловой точки, то поиск решения заключается в том, что игроки применяют не одну, а несколько чистых стратегий. В условиях неопределенности выбор каждой стратегии осуществляется с вероятностью p.

Пусть игра задана матрицей 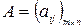. Обозначим вероятность выбора i -й стратегии 1-м игроком. Матрица (вектор) вероятностей выбора стратегий имеет вид , . Обозначим вероятность выбора j -й стратегии 2-м игроком. Матрица (вектор) вероятностей выбора стратегий имеет вид , .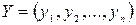

Если 1-й игрок выбирает i -ю стратегию, а 2-й выбирает j -ю, то вероятность выигрыша равна .

Математическое ожидание выигрыша 1-го игрока можно записать в виде или в матричной форме , где – транспонированная матрица.

Первый игрок должен найти такую стратегию , при которой достигается нижняя цена игры . Стратегия называется максиминной.

Второй игрок должен найти такую стратегию , при которой достигается верхняя цена игры . Стратегия называется минимаксной.

Теорема о минимаксе (теорема Неймана)

Каждая конечная матричная игра с нулевой суммой имеет по крайней мере одно решение и .

Если для стратегии , выполняется равенство , то число называется ценой игры, стратегии , – оптимальными стратегиями или оптимальным решением игры.

Для определения этих стратегий составим и решим 2 системы уравнений

,

где v – матрица-строка с элементами v,

,

где v – матрица-строка с элементами v,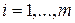

Пример 3

Найти смешанные оптимальные стратегии и цену игры, заданной матрицей .

Решение

Введем матрицу вероятностей 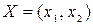. Составим систему уравнений:

.

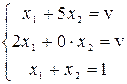Решение системы: , , .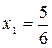

Оптимальная стратегия для первого игрока .

Введем матрицу вероятностей . Составим систему уравнений:

.

Решение системы: , , .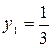

Оптимальная стратегия для второго игрока .

Цена игры .

Задание 2

Найти смешанные стратегии и цену игры, заданной матрицей А:

1) 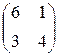; 2) ; 3) ; 4) ;
5) ; 6) ; 7) .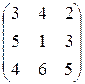  

4 РЕШЕНИЕ ИГРЫ 2 2

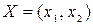Рассмотрим игру, заданную матрицей . Игра не имеет седловой точки. Для определения смешанных стратегий и запишем системы уравнений:

и .

Решение этих систем имеет вид:

; ; ;

; ; . (4.1)

Пример 4

Найти решение игры, заданной матрицей .

Решение

Воспользуемся формулой (4.1). Вычислим:

;

; ; ;

; ; ;

.

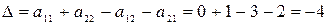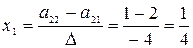Оптимальные стратегии , , цена игры .

Задание 3

Найти оптимальные стратегии и цену игры, заданной матрицей:

1) ; 2) 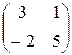; 3) ; 4) ; 5) .

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)