ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ИГРЫ

Графическим методом можно решать игры с матрицами размерност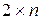и и .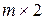

Пусть игра задана матрицей .

Смешанные стратегии 1-го игрока 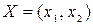, 2-го игрока . В системе координат XOY на оси OX откладываем отрезок ОВ=1. Через концы отрезка точку О и точку В проводим перпендикуляры к оси ОХ. Первый перпендикуляр совпадает с осью ОУ, второй проходит через точку В (1,0) параллельно оси ОУ. На первом перпендикуляре откладываем числа – выигрыши первого игрока, если он выбирал первую стратегию. На втором – числа 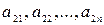– выигрыши первого игрока, если он выбрал вторую стратегию.

Полученные таким образом точки соединяем отрезками прямых, проходящих через две точки, лежащие на разных перпендикулярах и соответствующих j -й стратегии второго игрока.

Уравнения прямых , .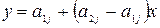

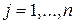Минимальный выигрыш первого игрока

,

где у – ординаты точек, лежащих на отрезках СМ и МD (рис. 1).

Ломаная СМD называется нижней границей выигрышей. Максимальный из минимальных выигрышей находится в точке М. Нижняя цена игры

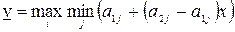
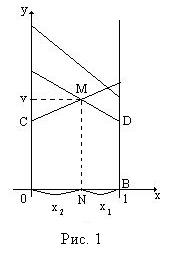или . Координаты точки 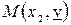можно найти по графику или по формулам (4.1).

Пусть 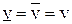. Прямым СМ и СD соответствуют два столбца в матрице А. Каждому из этих двух столбцов соответствуют вероятност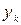и и , , .

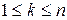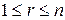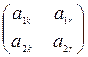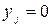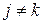Пусть матрица имеет вид . По формулам (4.1) находим . Вероятности при и .

Для игры с матрицей размерности 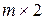меняем оси ОХ и ОУ местами. Оптимальное решение 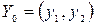находим на верхней границе выигрышей в точке min.

Пример 5

Найти оптимальное решение и цену игры, заданной матрицей

.

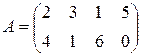Решение

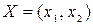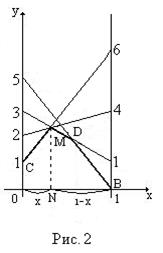
Найдем смешанные стратегии , 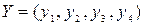графическим методом. В системе координат XOY на оси OX откладываем отрезок ОВ=1. Через концы отрезка проведем два перпендикуляра к оси ОХ. На первом откладываем числа 2, 3, 1, 5; на втором – числа 4, 1, 6, 0. Соединим полученные точки прямыми. Каждая прямая проходит через точки, соответствующие стратегиям второго игрока.

Нижняя граница выигрышей СМDB. Максимальный выигрыш на этой границе находится в точке М.

.

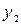Точка М лежит на пересечении прямых СМ и МD. Выпишем из матрицы А соответствующие столбцы . Этим столбцам соответствуют вероятности и 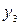. Найдем по формулам (4.1):

; ;

; ; ;

.

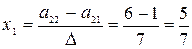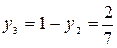Оптимальные смешанные стратегии , .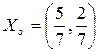

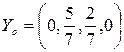Цена игры .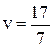

Пример 6

Найти оптимальное решение и цену игры, заданной матрицей .

Решение

Найдем смешанные стратегии 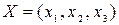, . В системе координат XOY поменяем оси местами, на оси OУ откладываем отрезок ОВ=1. Через концы отрезка проведем два перпендикуляра к оси ОУ. На первом откладываем проигрыши второго игрока, если он выбрал первую стратегию: 1, 2, 4. На втором перпендикуляре откладываем числа 0, 4, 3 – проигрыши второго игрока, если он выбрал вторую стратегию. Строим прямые, соединяющие точки, соответствующие выигрышам первого игрока, если он выбрал i -ю стратегию, i=1,2,3.

Верхняя граница игры СМD. Минимальный из максимальных проигрышей находится в точке М

.

Координаты точки 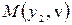можно найти графически:

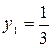, , или по формулам (4.1).

Выпишем строки матрицы А, соответствующие прямым СМ и MD, получим матрицу 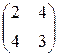соответствующие вероятности .

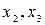Вычислим по формулам (4.1):

; ;

; ; ;

.

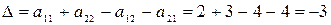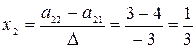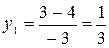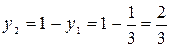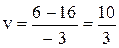Оптимальные смешанные стратегии , .

Цена игры .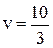

Задание 4

Найти графическим методом решение игры, заданной матрицей

1) 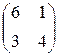;	2) 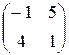;	3) 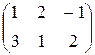;	4) ;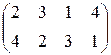
5) 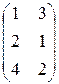;	6) ;	7) ;	8) .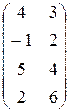

Поиск по сайту: