РЕШЕНИЕ ИГРЫ В ЧИСТЫХ СТРАТЕГИЯХ

ВВЕДЕНИЕ

В процессе своей деятельности человек сталкивается с различными конфликтными ситуациями. Выбор правильного поведения, стратегии позволяет разрешить эту ситуацию с наибольшим выигрышем.

Теория игр предлагает различные методы решения таких задач. В этой работе рассматриваются только матричные игры с конечным числом стратегий.

Рассмотрим простейшую стратегическую игру – парную игру двух игроков с нулевой суммой. Игра антагонистическая – выигрыш одного игрока является проигрышем другого. Игра конечная – каждый игрок имеет конечное число стратегий. Игра задается матрицей выигрышей или платежной матрицей 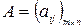. Выбор 1-м игроком i -й стратегии 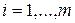соответствует выбору i -й строки матрицы 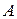. Выбор 2-м игроком j -й стратегии соответствует выбору j -го столбца матрицы 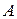. Элементу 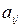– выигрыш 1-го и проигрыш
2-го игрока, если 1-й выбрал i -ю стратегию, а 2-й выбрал j -ю стратегию. Решение игры – выбор игроками наилучших для них стратегий.

И только игры с равнодушной «природой» заканчиваются выбором стратегии человеком.

РЕШЕНИЕ ИГРЫ В ЧИСТЫХ СТРАТЕГИЯХ

Рассмотрим игру, заданную матрицей 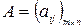. Первый игрок может выбрать одну из m стратегий. Рассматривая возможные выигрыши 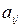, для каждой стратегии, он в наихудшем случае может получить выигрыш , 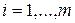. Из всех стратегий он может выбрать ту, при которой будет

.

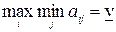Число называется нижней ценой игры и равно элементу 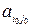матрицы 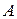, если первый игрок выбрал стратегию 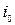, а второй – 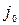. Стратегия 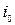называется максиминной.

Второй игрок, выбирая стратегию, стремится проиграть как можно меньше. В наихудшем случае при выборе j -й стратегии он может проиграть 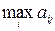. Из этих проигрышей он выбирает минимальный, т.е. выбирает стратегию 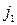, при которой

.

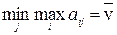Число называется верхней ценой игры и равно элементу 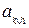матрицы 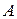, если первый игрок выбрал стратегию 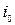. Стратегия 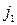называется минимаксной. Выбранные стратегии 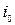, 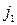называются чистыми стратегиями. Всегда справедливо соотношение .

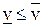Если при стратегиях 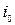, 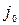имеет место равенство 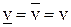, то число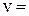 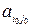называется ценой игры.

Пара стратегий максиминная 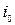и минимаксная 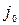называется оптимальным решением игры с ценой игры 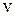. Пара стратегий (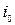, 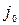) называется седловой точкой. Элемент 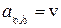называется седловым элементом матрицы 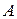. Игра называется игрой с седловой точкой. Игра с седловой точкой имеет решение в чистых стратегиях и относится к одноразовым играм.

Пример 1

Найти решение и цену игры, заданной матрицей .

Решение

В этой игре 1-й игрок имеет 3 стратегии, второй – 4. Первый игрок, рассматривая каждую стратегию, выбирает по строке минимальный выигрыш :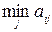

.

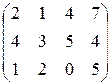
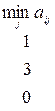
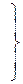
Из полученных 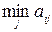выбираем максимальное число, получаем 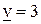– число, стоящее во 2-й строке. Нижняя цена игры 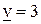, стратегия .

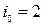Второй игрок, рассматривая каждую стратегию, выбирает в каждом столбце 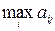– максимальный проигрыш.

.

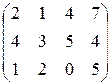
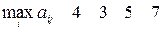
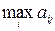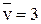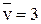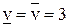Из полученных по столбцам выбрали минимальное и получили – число, стоящее во втором столбце. Минимаксная стратегия . Верхняя цена игры , . Элемент матрицы – седловой элемент. Пара оптимальных стратегий 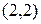– седловая точка. Цена игры .

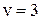Пример 2

Найти решение и цену игры, заданной матрицей .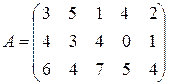

Решение

Первый игрок имеет 3 стратегии, второй – 5. Найдем седловую точку

,

, .

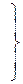
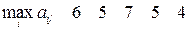
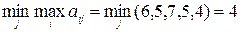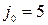Цена игры . Седловой элемент . Седловая точка (3,5). Оптимальное решение игры , 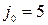. Отклонение от этих стратегий может привести к меньшему выигрышу для первого игрока и к большему проигрышу для второго.

Задание 1

Найти решение и цену игры, заданной матрицей:

1) ;	6) ;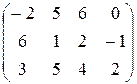
2) 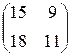;	7) ;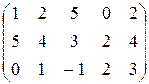
3) ;	8) ;
4) 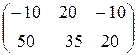;	9) ;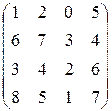
5) ;	10) .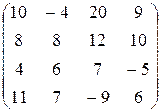

Поиск по сайту: