Математические проблемы теории тестов

Тема: Соціально–психологічні методи дослідження діагностики як засіб дослідження суб’єктивних механізмів та мотивації колективної та індивідуальної поведінки

Психологические тесты и социологические шкалы

Математические проблемы теории тестов

Впервые идею тестов выдвинул английский биолог Ф. Гальтон. Ему же принадлежит заслуга создания техники изучения индивидуальных различий на основе использования статистического метода. Гальтон искал способ математического описания тех закономерностей, которым подчиняются индивидуальные различия. В качестве метода он применил вариационную статистику.

В своих исканиях он опирался на работы А. Кетле – одного из создателей современной статистики. В своей работе «Социальная физика» (1835) Кетле показал, что формулы теории вероятности позволяют обнаружить факт подчинения поведения людей некоторым закономерностям. При анализе статистического материала он получил постоянные величины, дающие количественное описание таких актов человеческого поведения, как вступление в брак или самоубийство.

В интерпретации полученных данных Кетле исходил из идеи «среднего человека» – некоего идеала, отклонение которого изображается нормальным законом распределения. Если средняя является постоянной, то за ней должна стоять некая реальность, что позволяет предсказывать явления на основе статистических законов. Чтобы найти эти законы, безнадежно изучать каждого индивида в отдельности. Следует изучать поведение большой массы людей, используя метод вариационной статистики.

Давая статистический анализ биографических данных, Гальтон предлагал использовать законы Кетле для распределения человеческих способностей. Он считал, что существует средняя величина умственных способностей, так же как и средний рост.

Испытания, проводившиеся в антропологической лаборатории, организованной Гальтоном на Международной выставке в Лондоне в 1884 г., он назвал психологическими тестами. В широкий оборот этот термин вошел после выхода в свет в 1890 г. статьи его ученика – американского психолога Дж. М. Кеттелла – «Психологические тесты и измерения». В этой статье Кеттелл выдвинул требование статистического подхода – применения серии тестов к большому числу индивидов, полагая, что психология не сможет стать такой же точной наукой, как науки физические, если не будет базироваться на эксперименте и измерении.

Определенный сдвиг в этом направлении, по его мнению, может быть сделан путем применения серии психологических тестов к большому числу индивидов.

Разработанные Гальтоном приемы вариационной статистики вооружили психологию важным методическим средством. Среди них наиболее перспективным оказался метод исчисления коэффициента корреляции между переменными. Этот метод, усовершенствованный английским математиком К. Пирсоном и другими последователями Гальтона, внес в психологическую науку ценные математические методики, в результате использования которых возник в дальнейшем факторный анализ (работы Ч. Спирмена, Э. Л. Торндайка, Л. Терстона и др.). Постепенно совершенствовались методы статистической обработки результатов, контроля их надежности, обоснованности.

Начиная с 1905 г. французский психолог А. Бине в сотрудничестве с врачом Т. Симоном выполнили серию экспериментов по изучению умственных способностей людей различных возрастов. Проведенные на многих испытуемых (и тем самым подчиненные статистическим критериям), эти эксперименты превратились в тесты для определения уровня умственного развития. Индивидуальные различия испытывались уже не сами по себе, а в их отношении к возрастному ряду. Так возникла метрическая шкала интеллекта Бине – Симона, которая явилась первым стандартизированным тестом не только по унификации заданий и процедур их выполнения, но и по оценке полученных показателей. Это побудило ввести понятие умственного возраста – МА (Mental Age) в отличие от хронологического возраста – СА (Chronological Age). Их несовпадение считалось показателем либо умственной отсталости (МА ниже СА), либо одаренности (МА выше СА).

В 1912 г. немецкий психолог В. Штерн ввел понятие «коэффициент интеллекта» Intelligence Quotient – IQ как показатель темпа умственного развития, свойственного данному ребенку:

Коэффициент указывает на опережение или отставание умственного возраста относительно хронологического. Л. Терман, профессор психологии Стэнфордского университета в США, вместе со своими сотрудниками дважды (в 1916 и 1937 rr.) осуществил переработку шкалы Бине – Симона. Так возникла известная шкала Стэнфорд – Бине.

В связи с тем, что интеллект, как полагали, есть нечто увеличивающееся вместе с возрастом ребенка, и так как согласно всем предварительным стандартным оценкам чем старше ребенок, тем лучше его характеристики почти в любом единичном умственном тесте, то вполне естественно возраст был воспринят в качестве психологической меры интеллекта.

Кроме индивидуальных тестов, подобных тестам Бине, применяющих возраст в качестве измеряющей шкалы, существуют также групповые тесты, которые применяются более широко и используют в качестве единиц измерения тестовые вопросы. Тестовый балл – это взвешенное и невзвешенное число вопросов, на которые правильно ответил индивид с некоторой поправкой на случайность правильного ответа, если это необходимо. Тесты обычно состоят из большого числа разнородных вопросов, меняющихся по трудности от очень легких до очень трудных.

В настоящее время теория тестов представляет собой хорошо разработанную дисциплину, включающую в себя целый ряд проблем. При составлении тестов, анализе и интерпретации результатов учитываются пять основных требований, по Галликсену[1]. 1) составление и отбор тестовых вопросов; 2) присвоение балла каждому индивиду; 3) определение точности (надежности или ошибки измерения) тестовых баллов; 4) определение предсказующего значения тестовых баллов (обоснованности или ошибки оценивании); 5) сравнение этих результатов с результатами, полученными при использовании других тестов или других групп испытуемых.

Нас в первую очередь будут интересовать вопросы, связанные с математической стороной техники тестирования.

Наиболее общим видом теста является тест, в котором каждый вопрос представляет определенную задачу. Балл – это число «правильных» ответов в ограниченное время. Вопросы могут быть неодинаковыми по трудности или же концентрироваться на одном уровне трудности. В последнем случае одни испытуемые имеют более высокую вероятность ответов, чем другие и, следо-

вательно, более высокий уровень способности. Если вопросы имеют разные уровни трудности, то некоторые испытуемые могут ответить на более трудные вопросы и тем самым получить более высокий балл. Временной предел является еще одним источником разброса баллов, так как разные испытуемые работают с разной скоростью.

Самый обычный тип тестового балла – суммарный балл. Он основан на суммировании ответов определенной категории – правильных или неправильных.

Если мы предложим каждому из испытуемых тест из т вопросов, то результаты сможем представить в матрице вопросных баллов, в которой каждый столбец представляет соответствующий вопрос i, а каждая строка соответствующего испытуемого j.

Вопросы
	a	b	c	i	N
.
.
J
.
N
	1,0	0,9	0,9	0,7	0,6	0,6	0,5	0,4	0,3	0,3	0,2	0,1

Каждый испытуемый пытается ответить на каждый вопрос, и поэтому каждый вопросный балл 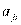будет либо 0, либо 1. Сумма вопросных баллов в строке – это общий балл испытуемого, сумма вопросных баллов в столбце – это число испытуемых, правильно ответивших на вопрос этого столбца. Таким образом, матрица является источником информации как относительно вопросов, так и относительно испытуемых. Поделив каждую сумму вопросных баллов в столбцах на N, мы получим долю испытуемых 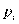, правильно ответивших на соответствующий вопрос.

Доля тех, кто правильно ответил на определенный вопрос, является простым способом описания трудности этого вопроса. Фактически это есть средняя баллов, и чем она ниже, тем труднее вопрос.

Необходимо отметить, что сумма вопросных средних равна средней общих баллов испытуемых, т.е.

=

где — средняя общих баллов в тесте ; – средняя баллов в каждом вопросе; – доля испытуемых, правильно ответивших на вопрос.

Дисперсия вопроса i определяется из уравнения

где – число испытуемых, правильно ответивших на вопрос, и . Стандартное отклонение вопроса таким образом будет следующим:

Предположим, что эмпирические баллы и исследуемая характеристика распределены нормально (рис. 12).

Пусть М и – средняя и дисперсия баллов; каждый индивид имеет свой балл как сумму правильных ответов. Этот эмпирический балл соответствует площади под кривой слева от некоторого значения х, которое определяется из таблиц нормального распределения. Каждый индивид получит характеристику в виде некоторой величины, измеренной в единицах о. Это так называемая Т-шкала. Иногда делают преобразование, с тем чтобы нормальное распределение имело характеристики М = 50, = 10. Это так называемая Т-шкала.

Выделяют два вида тестов: скорости и мощности.

В тестах скорости испытуемый не имеет времени ответить на все вопросы. В тестах мощности каждый испытуемый имеет возможность ответить на каждый вопрос. Но большинство тестов

находится между этими крайностями. Возникает серьезный вопрос, что измеряет тест, когда придается особое значение скорости в сравнении с мощностью.

В практике тестирования имеет существенное значение предоставление каждому испытуемому одного и того же ограниченного времени. Оптимальный предел времени определяется на основе некоторого ценностного суждения в зависимости от цели измерения. Важно, какие именно психологические свойства измеряются, когда времени много в сравнении с тем, когда времени мало. Как мы увидим, нельзя отделить проблему времени от проблемы трудности.

Существует предположение, согласно которому время и трудность в качестве переменных относительно взаимозаменяемы, т.е. мы можем измерить одну и ту же способность, либо определяя, сколько единиц работы можно произвести за единицу времени, либо устанавливая уровень трудности, который можно измерить в неограниченное время. Это значит, что индивид получит один и тот же балл (число успешных действий – ответы на вопросы) при различных комбинациях времени и уровней трудностей, поскольку произведение времени на трудность будет постоянным.

Терстоун сделал первую попытку решить эту проблему. Его рассуждения заключались в следующем. Он определил мощность индивида в качестве такого уровня трудности задач, при котором вероятность успеха равна 0,5 при условии, если дано бесконечное время. Бесконечное время есть все то время, какое практически затрачивает испытуемый для решения задачи. Вместе с этим определением мощности принимается предположение, что вероятность успеха представляется огивой трудности (рис. 13).

Диаграмма на рис. 13 представляет собой предполагаемую зависимость вероятности успеха от уровня трудности для разных отрезков времени: . В бесконечное время середина кривой приходится на уровень трудности А, который, по определению, является мерой мощности данного индивида при данном типе задачи. С уменьшением отрезков времени огива перемещается влево по шкале трудности.

Успех в качестве функции времени (для того же индивида при том же типе задачи) изображается на второй диаграмме при разных уровнях трудности: Можно предположить, что вероятность успеха по времени имеет вид восходящей огивы. В нулевое время вероятность успеха равна нулю. Задачи большой трудности решаются с вероятностью меньше, чем 0,5, даже после продолжительного времени.

Будут ли обычные суммарные баллы давать соответствующие

меры отдельным характеристикам индивидов, когда тест ограничен во времени? Измерение мощности индивида при выполнении задачи, как было определено, – это измерение его порогового балла в бесконечное время.

Гулликсен дал более строгое определение скорости и мощности тестов на основе статистических критериев. Сначала он определил следующие символы: – число неверных ответов; u – число вопросов без ответа; x = ω + и – общая ошибка балла (вопросы с неправильными ответами).

В чистом тесте скорости ω = 0, так что х = и, , а . Любой тест становится тестом скорости в той мере, в какой и достигают нуля, а М и достигают и соответственно.

В чистом тесте мощности и равны нулю, а и равны и соответственно.

Гулликсен[2] предложил критерий, согласно которому, если отношение очень мало, то тест по существу является тестом скорости, а если отношение очень мало, то это – тест мощности.

Поиск по сайту: