 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Середні величини, способи їх розрахунку
Середня величина – узагальнюючий показник, який характеризує типовий розмір ознаки у розрахунку на одиницю однорідної сукупності в конкретних умовах місця та часу.
У статистиці найбільш поширеними э два види середніх величин:
1. Середня арифметична;
2. Середня гармонічна.
Кожен із цих двох видів середніх величин може мати 2 форми:
1. Середня проста;
2. Середня зважена.
В результаті отримуємо 4 формули розрахунку середніх величин:
1. Середня арифметична проста:
, де х – значення середньої ознаки у кожної одиниці сукупності,
n – кількість одиниць сукупності;
2. Середня арифметична зважена:
, де х – значення середньої ознаки в кожній групі,
m(t) – кількість одиниць сукупності в кожній групі.;
3. Середня гармонічна проста
, де х – значення середньої ознаки у кожної одиниці сукупності,
m – кількість одиниць сукупності;
4. Середня гармонічна зважена
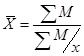, де х – значення середньої ознаки у кожної групі,
M – узагальнюючий (сумарний) показник.
У статистиці (на відміну від математики) в кожному конкретному випадку для розрахунку обирають одну єдиноможливу формулу розрахунку середньої величини. Вибір формули розрахунку здійснюється на основі так званої «логічної» формули, а також залежно від наявності вихідних даних.
«Логічна» формула – словесне описання способу розрахунку осереднюваної ознаки.
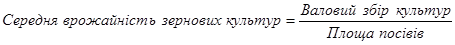
Вибір виду середньої величини здійснюється так:
1. Якщо відомий знаменник логічної формули і невідомий чисельник, то обирають середню арифметичну;
2. Якщо відомий чисельник логічної формули, а невідомий – знаменник, то обирають середню гармонічну.
Вибір форми середньої величини:
1. Якщо вихідна інформація є не згрупованою, то обирають середню просту;
2. Якщо вхідна інформація є згрупованою і ваги варіантів нерівні, то обирають середню зважену.
Алгоритм розрахунку середньої величини:
1. Записується логічна формула;
2. Обирається формула розрахунку середньої величини;
3. Здійснюється розрахунок середньої;
4. Робиться висновок.
Приклад:
Є такі дані по двох фермерських господарствах:
| Вид культур | Фермерське гос-во №1 | Фермерське гос-во №2 | ||
| Посівна площа, га m | Врожайність з 1 га, ц x | Валовий збір, ц M | Врожайність с 1 га, ц X | |
| Пшениця | ||||
| жито |
Визначити:
В якому господарстві середня врожайність зернових культур вища і на скільки %?
Фермерське господарство №1:
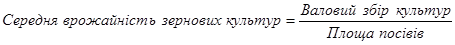
Оскільки відомий знаменник логічної формули, а невідомий – чисельник, то вид середньої – арифметична.
Оскільки вихідна інформація є згрупованою, причому ваги варіантів нерівні, то формою середньої буде зважена.
Таким чином, в даному випадку для розрахунку середньої величини потрібно обрати формулу середньої арифметичної зваженої:
У фермерському господарстві №1 з одного гектару посівів збирають в середньому 19,9 ц зернових культур.
Фермерське господарство №2:
Оскільки відомий чисельник логічної формули і невідомий знаменник, причому вхідна інформація згрупована і ваги нерівні, то для розрахунку потрібно обрати формулу середньої гармонічної зваженої:
Висновок: у фермерському господарстві №2 з 1 га посівів збирають в середньому 20,8 ц зернових культур.
Знайдемо відносну величину порівняння:
Висновок: у фермерському господарстві №2 середня врожайність зернових культур вища на 4,5%.
Поиск по сайту: