ГЛАВА 1 МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛОВ

В. И. Дмитриев

ПРИКЛАДНАЯ

ТЕОРИЯ

ИНФОРМАЦИИ

Москва 1989

ОГЛАВЛЕНИЕ

Введение…………………………………………………………………………….……..5

§ В.1 О понятии «информация»………………………………………………………..6

§ В.2 Этапы обращения информации…………………………………………………..8

§ В.3 Информационные системы……………………………………………………….9

§ В.4 Система передачи информации (основные понятия и определения)………...11

§ В.5 Уровни проблем передачи информации………………………………………...14

§ В.6 Теория информации……………………………………………………………...16

Глава 1 Математические модели сигналов…………………………………………...19

§ 1.1 Понятия сигнала и его модели…………………………………………………..19

§ 1.2 Формы представления детерминированных сигналов…………………………21

§ 1.3 Временная форма представления сигнала……………………………………...26

§ 1.4 Частотная форма представления сигнала……………………………………….28

§ 1.5 Соотношения между длительностью импульсов и шириной их спектров…...43 § 1.6 Спектральная плотность мощности детерминированного сигнала……….45 § 1.7 Функция автокорреляции детерминированного сигнала……………………...46

§ 1.8 Случайный процесс как модель сигнала………………………………………..48

§ 1.9 Стационарные и эргодические случайные процессы…………………………..53

§ 1.10 Спектральное представление случайных сигналов…………………………...56

§ 1.11 Частотное представление стационарных случайных сигналов……………58

Глава 2 Преобразование непрерывных сигналов в дискретные…………………..68

§ 2.1 Преимущества цифровой формы представления сигналов…………………...68

§ 2.2 Общая постановка задачи дискретизации………………………………………71

§ 2.3 Способы восстановления непрерывного сигнала………………………………74

§ 2.4 Критерии качества восстановления……………………………………………..76

§ 2.5 Методы дискретизации посредством выборок…………………………………77

§ 2.6 Равномерная дискретизация Теорема Котельникова………………………….79

§ 2.7 Теоретические и практические аспекты использования теоремы Котельникова...……………………………………………………………………………...84

§ 2.8 Дискретизация по критерию наибольшего отклонения………………………..86

§ 2.9 Адаптивная дискретизация………………………………………………………90

§ 2.10 Квантование сигналов…………………………………………………………..92

§ 2.11 Квантование сигналов при наличии помех……………………………………97

§ 2.12 Геометрическая форма представления сигналов……………………………...99

Глава 3 Количественная оценка информации………………………………………104

§ 3.1 Энтропия как мера неопределенности выбора………………………………..104

§ 3.2 Свойства энтропии……………………………………………………………...110

§ 3.3 Условная энтропия и ее свойства……………………………………………....114

§ 3.4 Энтропия непрерывного источника информации (дифференциальная энтропия)………………………………………………………………………………………119

§ 3.5 Свойства дифференциальной энтропии……………………………………..123

§ 3.6 Количество информации как мера снятой неопределенности……………….127

§ 3.7 Эпсилон энтропия случайной величины……………………………………..134

Глава 4. Информационные характеристики источника сообщений и канала связи.138

§ 4.1 Основные понятия и определения……………………………………………...138

§ 4.2 Информационные характеристики источника дискретных сообщений……..140

§ 4.3 Информационные характеристики дискретных каналов связи………………150

§ 4.4 Информационные характеристики источника непрерывных сообщений…...158

§ 4.5 Информационные характеристики непрерывных каналов связи…………….160

§ 4.6 Согласование физических характеристик сигнала и канала………………….165

§ 4.7 Согласование статистических свойств источника сообщений и канала связи…………………………………………………………………………………………167

Глава 5. Кодирование информации при передаче по дискретному каналу без помех……………………………………………………………………………………….174

§ 5.1 Кодирование как процесс выражения информации в цифровом виде……….174

§ 5.2 Технические средства представления информации в цифровой форме……..179

§ 5.3 Кодирование как средство криптографического закрытия информации……191

§ 5.4 Эффективное кодирование………………………………………………………196

§ 5.5 Технические средства кодирования и декодирования эффективных кодов…206

Глава 6. Кодирование информации при передаче по дискретному каналу с помехами………………………………………………………………………………………...210

§ 6.1 Основная теорема Шеннона о кодировании для канала с помехами………...210

§ 6.2 Разновидности помехоустойчивых кодов……………………………………...214

§ 6.3 Блоковые коды…………………………………………………………………...216

§ 6.4 Построение двоичного группового кода……………………………………….233

§ 6.5 Технические средства кодирования и декодирования для групповых кодов……………………………………………………………………………………….251

§ 6.6 Построение циклических кодов……………………………………………….255

§ 6.7 Выбор образующего многочлена по заданному объему кода и заданной корректирующей способности…………………………………………………………….260

§ 6.8 Технические средства кодирования и декодирования для циклических кодов……………………………………………………………………………………….270

§ 6.9 Коды Боуза—Чоудхури—Хоквингема…………………………………………291

§ 6.10 Итеративные коды……………………………………………………………...299

§ 6.11 Сверточные коды……………………………………………………………….305

Заключение……………………………………………………………………………...322

Список литературы……………………………………………………………………..323

Приложение……………………………………………………………………………..326

ВВЕДЕНИЕ

Эффективная организация обмена информацией приобретает все большее значение, прежде всего как условие успешной практической деятельности людей. Объем информации, необходимой для нормального функционирования современного общества, растет примерно пропорционально квадрату развития производительных сил. Доля рабочей силы, занятой вопросами обеспечения информацией, в развитых странах начинает превышать долю рабочей силы, занятой непосредственно в сфере производства. Применение методов и средств автоматизации на всех этапах обращения информации позволяет существенно повысить эффективность функционирования экономики страны и высвободить значительные трудовые ресурсы.

В соответствии с Постановлением ЦК КПСС и Совета Министров СССР об общегосударственной программе создания, развития производства и эффективного использования вычислительной техники и автоматизированных систем до 2000 г. в нашей стране намечен переход к широкой эксплуатации банков данных, локальных вычислительных сетей и других информационных систем. При этом особое значение приобретают системы связи и передачи данных, позволяющие обеспечить коллективный и удаленный доступ к средствам хранения и обработки информации.

Комплексная автоматизация процессов восприятия, преобразования, передачи, обработки и отображения информации с целью принятия оптимальных управляющих воздействий осуществляется в рамках создания автоматизированных систем управления (АСУ) на различных уровнях — от предприятия до народного хозяйства в целом.

Основой решения многих теоретических проблем создания АСУ является теория информации, предоставляющая возможности для комплексного информационного рассмотрения сложных систем.

Поскольку слово «информация» полисемично, возникает необходимость уточнения смысла этого понятия в рамках рассматриваемой теории.

§ В.1. О ПОНЯТИИ «ИНФОРМАЦИЯ»

Понятие «информация» является центральным понятием кибернетики. Оно используется и в теории информации, хотя основным понятием классической теории информации следует признать «количество информации», смысла которого коснемся несколько позже.

Имеется множество определений понятия информации от наиболее общего философского, (информация есть отражение реального мира) до наиболее узкого практического (информация есть все сведения, являющиеся объектом хранения, передачи и преобразования).

Некоторыми зарубежными авторами информация трактуется с идеалистических позиций в отрыве от материи как некоторая субстанция, занимающая промежуточное положение между материей и сознанием.

С позиций марксистской философии информация рассматривается как характеристика такого всеобщего свойства материи, как разнообразие. Такая трактовка находится в полном соответствии с известным положением В. И. Ленина о том, что вся материя обладает свойством отражения. Она четко выявляет взаимоотношения понятий «информация» и «отражение».

Информация — это отраженное разнообразие. В понятии «отражение» акцентируется внимание на воспроизведении содержания в целом, а в понятии «информация» — на воспроизведении одной его стороны — разнообразия. Следовательно, понятие «отражение» более широкое, более содержательное.

В рамках материалистической исходной посылки при конкретизации понятия «информация» имеют место расхождения по ряду существенных вопросов: информация — это свойство индивидуального объекта (процесса) или результат взаимодействия объектов (процессов)? Присуща ли информация всем видам материи или лишь определенным образом организованной материи? Существует ли информация в любых процессах или возникает только в процессах управления? Выдвинутое академиками Глушковым В. М. [3] и Колмогоровым А. Н. [10], а также английским философом Эшби и развиваемое советскими учеными понятие информации как характеристики внутренней организованности материальной системы (по множеству состояний, которые она может принимать) позволяет оценивать потенциальные возможности систем независимо от процесса передачи или восприятия информации. Здесь подчеркивается мысль о том, что информация существует независимо от того, воспринимается она или нет. Однако справедливо отмечается, что информация проявляется только при взаимодействии объектов (процессов).

Противоречия не возникает, если информацию рассматривать как свойство объекта в потенциальном смысле — свойство, которое проявляется лишь при взаимодействии объектов (процессов). Так, в куске каменного угля содержится информация о событиях, происшедших в далекие времена, однако эта информация проявляется лишь при взаимодействии с человеком. В книге Н. Винера «Кибернетика» [1] подчеркивается, что «информация есть информация, а не материя и не энергия». В отличие от них информация может возникать и исчезать. В указанном примере с информацией в куске каменного угля она исчезнет, когда этот кусок каменного угля сгорит.

Весьма распространенным является также мнение о том, что информация присуща лишь определенным образом организованной материи, в которой возможны процессы управления. Сторонники этой точки зрения под информацией подразумевают только то, что воспринято и осмыслено, т. е. то, что целесообразно использовать для управления. Нетрудно заметить, что вопрос о существовании информации здесь неправомерно отождествляется с вопросом о способности объекта к восприятию и использованию информации. При таком подходе легко сойти на позиции субъективизма, ставящего объективно существующее в зависимость от воспринимающего субъекта.

При всех различиях в трактовке понятия информации, бесспорно то, что проявляется информация всегда в материально-энергетической форме в виде сигналов. Информацию, представленную в формализованном виде, позволяющем осуществить ее обработку с помощью технических средств, называют данными.

§ В.2. ЭТАПЫ ОБРАЩЕНИЯ ИНФОРМАЦИИ

Хотя роль информации может ограничиваться неопределенным эмоциональным воздействием на человека, в чисто технических (автоматических) и человеко-машинных (автоматизированных) системах она чаще всего используется для выработки управляющих воздействий. При обращении информации в системах можно выделить отдельные этапы [26]. Так как материальным носителем информации является сигнал, то реально это будут этапы обращения и преобразования сигналов (рис. В.1).

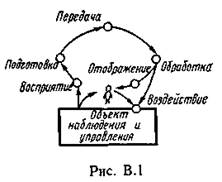
На этапе восприятия информации осуществляется целенаправленное извлечение и анализ информации о каком-либо объекте (процессе), в результате чего формируется образ объекта, проводятся его опознание и оценка. При этом необходимо отделить интересующую нас в данном случае информацию от мешающей (шумов), что в ряде случаев связано со значительными трудностями. Простейшим видом восприятия является различение двух противоположных состояний: наличия («да») и отсутствия («нет»), более сложным — измерение.

На этапе подготовки информации проводятся такие операции, как нормализация, аналого-цифровое преобразование, шифрование. Иногда этот этап рассматривается как вспомогательный на этапе восприятия. В результате восприятия и подготовки получается сигнал в форме, удобной для передачи или обработки.

На этапах передачи и хранения информация пересылается либо из одного места в другое, либо от одного момента времени до другого. Поскольку теоретические задачи, возникающие на этих этапах, близки друг другу, этап хранения информации часто в самостоятельный этап не выделяется. При этом передача информации получает более широкое толкование. Для передачи на расстояние используются каналы различной физической природы, самыми распространенными из которых являются электрические и электромагнитные. В последнее десятилетие получил признание также перспективный оптический канал. Для хранения информации используются в основном полупроводниковые и магнитные носители. Извлечение сигнала на выходе канала, подверженного действию шумов, носит характер вторичного восприятия.

На этапах обработки информации выявляются ее общие и существенные взаимозависимости, представляющие интерес для системы. Преобразование информации на этапе обработки (как и на других этапах) осуществляется либо средствами информационной техники, либо человеком. Если процесс обработки формализуем, он может выполняться техническими средствами. В современных сложных системах эти функции возлагаются на ЭВМ и микропроцессоры. Если процесс обработки не поддается формализации и требует творческого подхода, обработка информации осуществляется человеком. В системах управления важнейшей целью обработки является решение задачи выбора управляющих воздействий (этап принятия решения).

Этап отображения информации должен предшествовать этапам, связанным с участием человека. Цель этапа отображения — предоставить человеку нужную ему информацию с помощью устройств, способных воздействовать на его органы чувств.

На этапе воздействия информация используется для осуществления необходимых изменений в системе.

§ В. 3. ИНФОРМАЦИОННЫЕ СИСТЕМЫ

Совокупность средств информационной техники и людей, объединенных для достижения определенных целей или для управления, образуют автоматизированную информационную систему, к которой по мере надобности подключаются абоненты (люди или устройства), поставляющие и использующие информацию.

Информационные системы, действующие без участия человека, называют автоматическими. За человеком в таких системах остаются функции контроля и обслуживания.

Автоматизированная информационная система становится автоматизированной системой управления (АСУ), если поставляемая информация извлекается из какого-либо объекта (процесса), а выходная используется для целенаправленного изменения состояния того же объекта (процесса), причем абонентом, использующим информацию для выбора основных управляющих воздействий (принятия решения), является человек. Объектом могут быть техническая система, экологическая среда, коллектив людей. Существуют АСУ, в которых отдельные функции управления возлагаются на технические средства, в основном на ЭВМ и микропроцессоры.

Автоматизированные информационные системы и АСУ нашли широкое применение во всех отраслях народного хозяйства в первую очередь как информационно-справочные и информационно-советующие системы, системы управления технологическими процессами и коллективами людей. Большинство из них являются локальными системами и функционируют на уровне предприятий и учреждений. В настоящее время происходит интенсивный процесс интеграции таких систем в системы производственных объединений и далее — в отраслевые и ведомственные системы.

Системы более высокого уровня становятся территориально рассредоточенными, иерархичными как по функциональному принципу, так и по реализации их техническими средствами. Обеспечение взаимодействия территориально рассредоточенных систем требует протяженных высокоскоростных и надежных каналов связи, а увеличение объема обрабатываемой информации — ЭВМ высокой производительности. Это привело к необходимости коллективного использования дорогостоящих средств автоматизации (ЭВМ и линий связи) и обрабатываемой информации (банков и баз данных). Техническое развитие, как самих электронных вычислительных машин, так и средств связи позволило, решить эту проблему путем перехода к созданию распределенных информационно-вычислительных сетей коллективного пользования.

Централизация различных видов информации в одной сети дает возможность использовать ее для решения широкого спектра задач, связанных с административным управлением, планированием, научными исследованиями, конструкторскими разработками, технологией производства, снабжением, учетом и отчетностью. В недалеком будущем использование информационно-вычислительных сетей позволит отказаться от традиционных форм массового общения, таких, как телефон, телеграф, почта, отдельные справочные службы.

Наиболее распространенными информационными системами являются системы, обеспечивающие передачу информации из одного места в другое (системы связи) и от одного момента времени до другого (системы хранения информации). Обе разновидности систем передачи информации имеют много общего в принципиальных вопросах обеспечения эффективности функционирования. Их применяют как самостоятельные системы и как подсистемы в составе любых более сложных информационных систем. Совокупность таких подсистем в информационно-вычислительной сети образует ее основное ядро — сеть передачи данных.

Последующее изложение будем вести в основном применительно к системам связи, подразумевая возможность интерпретации основных понятий и выводов к другим информационным системам.

§ В.4. СИСТЕМА ПЕРЕДАЧИ ИНФОРМАЦИИ

(ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ)

Структурная схема одноканальной системы передачи информации приведена на рис. В.2. Информация поступает в систему в форме сообщений. Под сообщением понимают совокупность знаков или первичных сигналов, содержащих информацию. Источник сообщений в общем случае образует совокупность источника информации ИИ (исследуемого или наблюдаемого объекта) и первичного преобразователя ПП (датчика, человека-оператора и т.п.), воспринимающего информацию о его состояниях или протекающем в нем процессе. Различают дискретные и непрерывные сообщения.

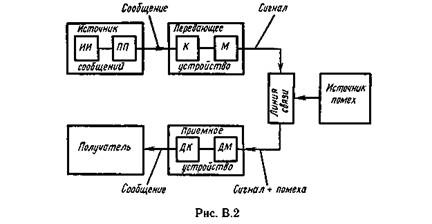
Дискретные сообщения формируются в результате последовательной выдачи источником отдельных элементов — знаков. Множество различных знаков называют алфавитом источника сообщений, а число знаков — объемом алфавита. В частности, знаками могут быть буквы естественного или искусственного языка, удовлетворяющие определенным правилам взаимосвязи. Распространенной разновидностью дискретных сообщений являются данные.

Непрерывные сообщения не разделимы на элементы. Они описываются функциями времени, принимающими непрерывное множество значений. Типичными примерами непрерывных сообщений могут служить речь, телевизионное изображение. В ряде систем связи непрерывные сообщения с целью повышения качества передачи преобразуются в дискретные.

Для передачи сообщения по каналу связи ему необходимо поставить в соответствие определенный сигнал. В информационных системах под сигналом понимают физический процесс, отображающий (несущий) сообщение. Преобразование сообщения в сигнал, удобный для передачи по данному каналу связи, называют кодированием в широком смысле слова. Операцию восстановления сообщения по принятому сигналу называют декодированием.

Так как число возможных дискретных сообщений при неограниченном увеличении времени стремится к бесконечности, а за достаточно большой промежуток времени весьма велико, то ясно, что создать для каждого сообщения свой сигнал практически невозможно. Однако, поскольку дискретные сообщения складываются из знаков, имеется возможность обойтись конечным числом образцовых сигналов, соответствующих отдельным знакам алфавита источника.

Для обеспечения простоты и надежности распознавания образцовых сигналов их число целесообразно сократить до минимума. Поэтому, как правило, прибегают к операции представления исходных знаков в другом алфавите с меньшим числом знаков, называемых символами. При обозначении этой операции используется тот же термин «кодирование», рассматриваемый в узком смысле. Устройство, выполняющее такую операцию, называют кодирующим или кодером К. Так как алфавит символов меньше алфавита знаков, то каждому знаку соответствует некоторая последовательность символов, которую назовем кодовой комбинацией. Число символов в кодовой комбинации называют ее значностью, число ненулевых символов — весом.

Аналогично, для операции сопоставления символов со знаками исходного алфавита используется термин «декодирование». Техническая реализация ее осуществляется декодирующим устройством или декодером ДК. В простейшей системе связи кодирующее, а следовательно, и декодирующее устройство может отсутствовать.

Передающее устройство осуществляет преобразование непрерывных сообщений или знаков в сигналы, удобные для прохождения по конкретной линии связи (либо для хранения в некотором запоминающем устройстве). При этом один или несколько параметров выбранного носителя изменяют в соответствии с передаваемой информацией. Такой процесс называют модуляцией. Он осуществляется модулятором М.. Обратное преобразование сигналов в символы производится демодулятором ДМ.

Под линией связи понимают любую физическую среду (воздух, металл, магнитную ленту и т. п.), обеспечивающую поступление сигналов от передающего устройства к приемному. Сигналы на выходе линии связи могут отличаться от переданных вследствие затухания, искажения и воздействия помех. Помехами называют любые мешающие возмущения, как внешние (атмосферные помехи, промышленные помехи), так и внутренние (источником которых является сама аппаратура связи), вызывающие случайные отклонения принятых сигналов от переданных. Эффект воздействия помех на различные блоки системы стараются учесть эквивалентным изменением характеристик линии связи. Поэтому источник помех условно относят к линии связи.

Из смеси сигнала, и помехи приемное устройство выделяет сигнал и посредством декодера восстанавливает Сообщение, которое в общем случае может отличаться от посланного. Меру соответствия принятого сообщения посланному называют верностью передачи. Обеспечение заданной верности передачи сообщений — важнейшая цель системы связи.

Принятое сообщение с выхода системы связи поступает к абоненту-получателю, которому была адресована исходная информация.

Совокупность средств, предназначенных для передачи сообщений, называют каналом связи. Для передачи информации от группы источников, сосредоточенных в одном пункте, к группе получателей, расположенных в другом пункте, часто целесообразно использовать только одну линию связи, организовав на ней требуемое число каналов. Такие системы называют многоканальными.

§ В.5. УРОВНИ ПРОБЛЕМ ПЕРЕДАЧИ ИНФОРМАЦИИ

Обмен информацией предполагает использование некоторой системы знаков, например, естественного или искусственного (формального) языка. Информация о непрерывных процессах также может быть выражена посредством знаков.

Изучение знаковых систем наукой о знаках, словах и языках (семиотикой) проводится, по крайней мере, на трех уровнях:

1. на синтактическом уровне рассматривают внутренние свойства текстов, т. е. отношения между знаками, отражающие структуру данной знаковой системы. Внешние свойства текстов изучают на семантическом и прагматическом уровнях;

2. на семантическом уровне анализируют отношения между знаками и обозначаемыми ими предметами, действиями, качествами, т. е. смысловое содержание текста, его отношение к источнику информации;

3. на прагматическом уровне рассматривают отношения между текстом и теми, кто его использует, т. е. потребительское содержание текста, его отношение к получателю.

Учитывая определенную взаимосвязь проблем передачи информации с уровнями изучения знаковых систем, их разделяют на проблемы синтактического, семантического и прагматического уровней.

Проблемы синтактического уровня касаются создания теоретических основ построения систем связи, основные показатели функционирования которых были бы близки к предельно возможным, а также совершенствования существующих систем с целью повышения эффективности их использования. Это чисто технические проблемы совершенствования методов передачи сообщений и их материального воплощения — сигналов. Иначе говоря, на этом уровне интересуют проблемы доставки получателю сообщений как совокупности знаков, при этом полностью абстрагируемся от их смыслового и прагматического содержания [16].

Основу интересующей нас теории информации составляют результаты решения ряда проблем именно этого уровня. Она опирается на понятие «количество информации», являющееся мерой частоты употребления знаков, которая никак не отражает ни смысла, ни важности передаваемых сообщений. В связи с этим иногда говорят, что теория информации находится на синтактическом уровне.

Проблемы семантического уровня связаны с формализацией смысла передаваемой информации, например, введением количественных оценок близости информации к истине, т. е. оценок ее качества. Эти проблемы чрезвычайно сложны, так как смысловое содержание информации больше зависит от получателя, чем от семантики сообщения, представленного в каком-либо языке. Информация заложена в сообщении, но проявляется она только при взаимодействии с получателем, так как может быть зашифрована. Из полученной телеграммы адресат может извлечь совершенно другую информацию по сравнению с той, которая будет доступна работнику телеграфа. Если получатель — человек, то и незашифрованное (или правильно расшифрованное) сообщение может быть понято по-разному. Основная причина состоит в том, что различное понимание того или иного слова может сильно изменить смысл переданной информации. Кроме того, восприятие человеком информации зависит от его эмоционального состояния, накопленного жизненного опыта и других факторов.

Следует отметить, что мы еще не умеем измерять семантическую информацию. Имевшие место подходы к ее измерению пока носили весьма частный характер.

На прагматическом уровне интересуют последствия от получения и использования данной информации абонентом. Проблемы этого уровня — это проблемы эффективности. Основная сложность здесь состоит в том, что ценность или потребительская стоимость информации может быть совершенно различной для различных получателей. Кроме того, она существенно зависит от истинности и прогностичности информации, своевременности ее доставки и использования. Высокие требования в отношении скорости доставки информации часто диктуются тем, что управляющие воздействия должны осуществляться в реальном масштабе времени, т. е. со скоростью изменения состояния управляемых объектов или процессов. Задержки в доставке или использовании информации могут иметь катастрофические последствия.

В направлении количественного определения прагматического содержания информации сделаны лишь первые шаги. Предложен ряд количественных мер, которые еще недостаточно конструктивны, чтобы найти широкое практическое применение. В связи с созданием информационно-вычислительных сетей ведутся интенсивные исследования в области оценки старения информации, т. е. потери ее ценности в процессе доставки [26].

§ Β.6. ТЕОРИЯ ИНФОРМАЦИИ

Возникновение теории информации связывают обычно с появлением фундаментальной работы американского ученого К. Шеннона «Математическая теория связи» (1948). Однако в теорию информации органически вошли и результаты, полученные другими учеными, например Р. Хартли, впервые предложившим количественную меру информации (1928), акад. В. А. Котельниковым, сформулировавшим важнейшую теорему о возможности представления непрерывной функции совокупностью ее значений в отдельных точках отсчета (1933) и разработавшим оптимальные методы приема сигналов на фоне помех (1946), акад. А. Н. Колмогоровым, внесшим огромный вклад в статистическую теорию колебаний, являющуюся математической основой теории информации (1941).

В последующие годы теория информации получила дальнейшее развитие в трудах советских ученых (А. Н. Колмогорова, А. Я. Хинчина, В. И. Сифорова, Р. Л. Добрушина, М. С. Пинскера, А. Н. Железнова, Л. М. Финка и др.), а также ряда зарубежных ученых (В. Макмиллана, А. Файнстейна, Д. Габора, Р. М. Фано, Ф. М. Вудворта, С. Гольдмана, Л. Бриллюэна и др.).

К теории информации в ее узкой классической постановке относят результаты решения ряда фундаментальных теоретических вопросов, касающихся повышения эффективности функционирования систем связи. Это в первую очередь:

1. анализ сигналов как средства передачи сообщений, включающий вопросы оценки переносимого ими «количества информации»;

2. анализ информационных характеристик источников сообщений и каналов связи и обоснование принципиальной возможности кодирования и декодирования сообщений, обеспечивающих предельно допустимую скорость передачи сообщений по каналу связи, как при отсутствии, так и при наличии помех.

Прикладные результаты приводятся здесь только для пояснения основ теории. При более широкой трактовке теории информации результаты рассмотрения указанных вопросов составляют ее основу.

Если расширение связано с приложением теории в технике связи — рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации.

Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В этом случае к ней относят все локальные проблемы систем связи, включая, например, проблему оптимального приема и др.

В соответствии с третьей крайней точкой зрения к компетенции теории информации относят все проблемы и задачи, в формулировку которых входит понятие информации. Ее предметом считают изучение процессов, связанных с получением, передачей, хранением, обработкой и использованием информации. В такой постановке она затрагивает проблемы многих наук (в частности, кибернетики, биологии, психологии, лингвистики, педагогики) на всех трех уровнях (синтактическом, семантическом и прагматическом).

Попытки широкого использования идей теории информации в различных областях науки связаны с тем, что в основе своей эта теория математическая. Основные ее понятия (энтропия, количество информации, пропускная способность) определяются только через вероятности событий, которым может быть приписано самое различное физическое содержание. Подход к исследованиям в других областях науки с позиций использования основных идей теории информации получил название теоретико-информационного подхода. Его применение в ряде случаев позволило получить новые теоретические результаты и ценные практические рекомендации. Однако не редко такой подход приводит к созданию моделей процессов, далеко не адекватных реальной действительности. Поэтому в любых исследованиях, выходящих за рамки чисто технических проблем передачи и хранения сообщений, теорией информации следует пользоваться с большой осторожностью. Особенно это касается моделирования умственной деятельности человека, процессов восприятия и обработки им информации.

Содержание данной книги ограничивается теорией информации в первой трактовке, вопросами теории и практики кодирования и некоторыми примерами применения теории информации в областях, смежных с техникой связи.

Прикладная теория информации является одним из фундаментальных курсов при подготовке инженеров – системотехников, специализирующихся в области автоматизированных систем управления. Функционирование таких систем существенным образом связано с получением, подготовкой, передачей, хранением и обработкой информации, поскольку без осуществления этих этапов невозможно принять правильное решение, а, следовательно, и осуществить требуемое управляющее воздействие, которое является конечной целью функционирования системы.

Контрольные вопросы

1. В чем сущность принципиальных различий в трактовке понятия информации?

2. Каковы основные этапы обращения информации?

3. Охарактеризуйте разновидности информационных систем и тенденции их развития.

4. Совокупность, каких объектов составляет систему передачи информации?

5. Что понимают под сообщением и сигналом?

6. В чем различие между линией и каналом связи?

7. Объясните разницу в уровнях проблем передачи информации.

8. Каковы основные задачи теории информации?

9. В чем сущность теоретико-информационного подхода к исследованиям?

ГЛАВА 1 МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛОВ

§ 1.1. ПОНЯТИЯ СИГНАЛА И ЕГО МОДЕЛИ

Как указывалось во введении, понятие «сигнал» имеет неоднозначное толкование. В широком смысле слова под сигналом понимают материальный носитель информации. При этом к сигналам относят как естественные сигналы, так и сигналы, специально создаваемые с определенной целью. Естественными являются, например, световые сигналы, позволяющие видеть окружающий мир, космические сигналы. Примером специально создаваемых могут служить сигналы, генерируемые с целью извлечения информации об изменениях в объекте или процессе (эталонные сигналы).

В дальнейшем понятие «сигнал», если это не оговорено специально, будет использоваться в узком смысле как сигнал, специально создаваемый для передачи сообщения в информационной системе. Материальную основу сигнала составляет какой-либо физический объект или процесс, называемый носителем (переносчиком) информации (сообщения). Носитель становится сигналом в процессе модуляции. Параметры носителя, изменяемые во времени в соответствии с передаваемым сообщением, называют информативными.

В качестве носителей информации используются колебания различной природы, чаще всего гармонические, включая частный случай — постоянное состояние (ω = 0). В технических информационных системах наиболее широкое распространение получили носители в виде электрического напряжения или тока. Поэтому, рассматривая в дальнейшем модели сигналов, для конкретности, будем соотносить их с электрическими сигналами.

В носителе u(t) = const имеется только один информативный параметр — уровень (например, уровень напряжения). При использовании гармонических электрических колебаний информативными могут стать такие параметры, как амплитуда, частота, фаза. Колебания принято подразделять на детерминированные и случайные.

Детерминированными называют колебания, которые точно определены в любые моменты времени.

Случайные колебания отличаются тем, что значения их некоторых параметров предсказать невозможно. Они могут рассматриваться как сигналы, когда несут интересующую нас информацию (случайные сигналы), или как помехи, когда мешают наблюдению интересующих нас сигналов.

При изучении общих свойств каналов связи, сигналов и помех мы отвлекаемся от их конкретной физической природы, содержания и назначения, заменяя моделями. Модель — это выбранный способ описания объекта, процесса или явления, отражающий существенные с точки зрения решаемой задачи факторы.

Задачи повышения эффективности функционирования информационных систем связаны с установлением количественных соотношений между основными параметрами, характеризующими источник информации и канал связи. Поэтому при исследовании используют математические модели. Математическое моделирование может быть реализовано различными методами в зависимости от способа, которым определяются интересующие нас показатели.

Фундаментальные исследования базируются на методе аналитического моделирования, заключающемся в создании совокупности математических соотношений, позволяющих выявить зависимости между параметрами модели в общем виде. При этом широко используются модели, параметры которых противоречат физическим свойствам реальных объектов. Например, модель сигнала часто представляется суммой бесконечного числа функций, имеющих неограниченную продолжительность (синусоид). Поэтому важно обращать внимание на условия, при которых это не мешает получать результаты, соответствующие наблюдаемым в действительности.

Так как источник сообщений выдает каждое сообщение с некоторой вероятностью, то предсказать точно изменения значения информативного параметра невозможно. Следовательно, сигнал принципиально представляет собой случайное колебание и его аналитической моделью может быть только случайный процесс, определяемый вероятностными характеристиками.

Тем не менее, в случае детерминированного колебания условно так же говорят о детерминированном сигнале. Такой сигнал отображает известное сообщение, которое нет смысла передавать. Ему соответствует модель в виде функции, полностью определенной во времени.

Изучение моделей детерминированных сигналов необходимо по многим причинам. Важнейшая из них заключается в том, что результаты анализа детерминированных сигналов являются основой для изучения более сложных случайных сигналов. Это обусловлено тем, что детерминированный сигнал может рассматриваться как элемент множества детерминированных функций, составляющих в совокупности случайный процесс. Детерминированное колебание, таким образом, представляет собой вырожденную форму случайного процесса со значениями параметров, известными в любой момент времени с вероятностью, равной единице. Детерминированные сигналы имеют и самостоятельное значение. Они специально создаются для целей измерения, наладки и регулирования объектов информационной техники, выполняя роль эталонов.

§ 1.2. ФОРМЫ ПРЕДСТАВЛЕНИЯ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ

В зависимости от структуры информационных параметров сигналы подразделяют на дискретные, непрерывные и дискретно-непрерывные.

Сигнал считают дискретным по данному параметру, если число значений, которое может принимать этот параметр, конечно (или счетно). Если множество возможных значений параметра образует континуум, то сигнал считают непрерывным по данному параметру. Сигнал, дискретный по одному параметру и непрерывный по другому, называют дискретно-непрерывным.

В соответствии с этим существуют следующие разновидности математических представлений (моделей) детерминированного сигнала:

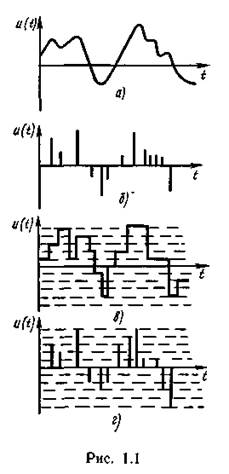
1. непрерывная функция непрерывного аргумента, например непрерывная функция времени (рис. 1.1, а);

2. непрерывная функция дискретного аргумента, например функция, значения которой отсчитывают только в определенные моменты времени (рис. 1.1,б);

3. дискретная функция непрерывного аргумента, например функция времени, квантованная по уровню (рис. 1.1, в);

4. дискретная функция дискретного аргумента, например функция, принимающая одно из конечного множества возможных значений (уровней) в определенные моменты времени (рис. 1.1, г).

Рассматриваемые модели сигналов в виде функций времени предназначены в первую очередь для анализа формы сигналов. Желательно найти такое представление сигнала, которое облегчает задачи исследования прохождения реальных сигналов, часто имеющих достаточно сложную форму, через интересующие нас системы. С этой целью сложные сигналы представляются совокупностью элементарных (базисных) функций, удобных для последующего анализа.

Наиболее широкий класс исследуемых систем — это инвариантные во времени линейные системы.

При анализе прохождения сложного сигнала u(t) через такие системы его представляют в виде взвешенной суммы базисных функций (t) (или соответствующего ей интеграла):

где [ 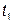, 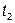] — интервал существования сигнала.

При выбранном наборе базисных функций сигнал u(t) полностью определяется совокупностью безразмерных коэффициентов 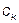. Такие совокупности чисел называют дискретными спектрами сигналов.

На интервале 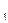[t , t ] выражение (1.1) справедливо как для сигналов, неограниченных во времени, так и для сигналов конечной длительности. Однако за пределами интервала 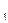[t , t ] сигнал конечной длительности не равен нулю, так как он представляется суммой в том случае, если условно считается периодически продолжающимся. Поэтому, когда для ограниченного во времени сигнала необходимо получить представление, справедливое для любого момента времени, используется интеграл:

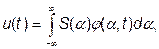(1.2)

где φ(α, t) — базисная функция с непрерывно изменяющимся параметром .

В этом случае имеется непрерывный (сплошной) спектр сигнала, который представляется спектральной плотностью S(). Размерность ее обратна размерности . Аналогом безразмерного коэффициента 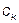здесь является величина S()d .

Совокупность методов представления сигналов в виде (1.1) и (1.2) называют обобщенной спектральной теорией сигналов. В рамках линейной теории спектры являются удобной аналитической формой представления сигналов.

Для теоретического анализа базисные функции 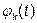нужно выбирать так, чтобы они имели простое аналитическое выражение, обеспечивали быструю сходимость ряда (1.1) для любых сигналов u(t) и позволяли легко вычислять значения коэффициентов 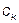. Базисные функции не обязательно должны быть действительными, их число может быть неограниченным .

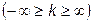В случае практической аппроксимации реального сигнала совокупностью базисных сигналов решающее значение приобретает простота их технической реализации. Сигнал представляется суммой ограниченного числа 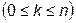действительных линейно независимых базисных функций (сигналов).

Ортогональные представления сигналов. Вычисление спектральных составляющих сигнала существенно облегчается при выборе в качестве базиса системы ортогональных функций.

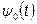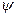
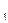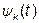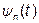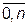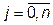Систему функций , (t),..., ,..., ,..., называют ортогональной на отрезке [t , t ], если для всех k = ; , за исключением случая k = j, удовлетворяется условие:

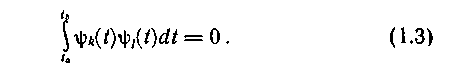
Эта система функций будет ортонормированной (ортонормальной), если для всех 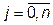справедливо соотношение

Если соотношение (1.4) не выполняется и

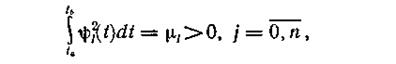
то систему можно нормировать, умножая функции на 1/ .

Определим коэффициенты 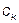при представлении сигнала u(t) совокупностью ортонормированных функций в виде

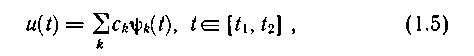
предполагая, что интервал 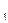[t , t ] лежит внутри отрезка ортогональности [t , t ].

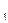Правую и левую части уравнения (1.5) умножаем на и интегрируем, на интервале [t , t ]:

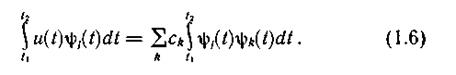
В силу справедливости условия (1.3) все интегралы в правой части выражения (1.6) при 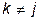будут равны 0. При k = j в соответствии с (1.4) интеграл равен 1. Следовательно,

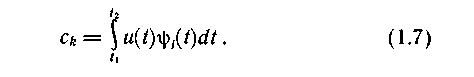
В теоретических исследованиях обычно используют полные системы ортогональных функций, обеспечивающие сколь угодно малую разность непрерывной функции u(t) и представляющего ее ряда при неограниченном увеличении числа его членов. Разность оценивают по критерию

При этом говорят о среднеквадратической сходимости ряда к функции u(t).

Широко известной ортонормированной системой является совокупность тригонометрических функций кратных аргументов:

Она ортонормальна на отрезке [-π, π].Так как соответствующее разложение исторически появилось первым и было названо рядом Фурье, то соотношение (1.5) часто именуют обобщенным рядом Фурье, а значения 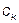- обобщенными коэффициентами Фурье.

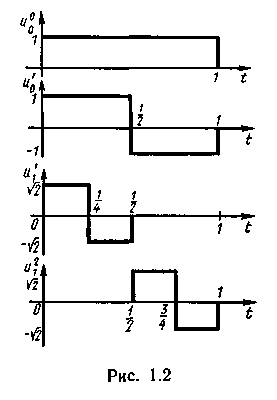На рис. 1.2 приведена система функций Хаара, ортонормированность которых на интервале 0-1 также очевидна. Известны представления сигналов по системам ортогональных базисных многочленов Котельникова, Чебышева, Лаггера, Лежандра и др., а также неортогональные разложения по функциям Лагранжа, Тейлора и др .

Обобщенная спектральная теория облегчает решение проблемы обоснованного выбора базисных функций для конкретных задач анализа процессов, происходящих при формировании и прохождении сигналов через те или иные звенья информационной системы.

§ 1.3. ВРЕМЕННАЯ ФОРМА ПРЕДСТАВЛЕНИЯ СИГНАЛА

Временным представлением сигнала называют такое разложение сигнала u(t), при котором в качестве базисных функций используются единичные импульсные функции — дельта-функции. Математическое описание такой функции задается соотношениями

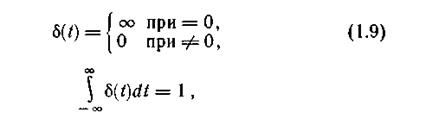
где δ(t) — дельта-функция, отличная от нуля в начале координат (при t = 0).

Для более общего случая, когда дельта-функция отличается от нуля в момент времени t= 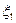(рис. 1.3), имеем

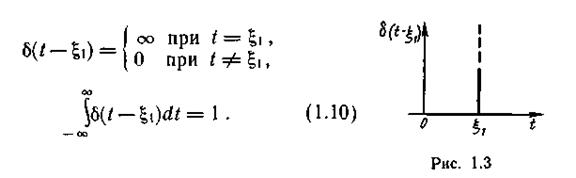
Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (1.10), с помощью дельта-функции можно выразить значение реального сигнала u(t) в конкретный момент времени ξι:

Равенство (1.11) справедливо для любого текущего момента времени t. Заменив ξι на t и приняв в качестве переменной интегрирования ξ, получим

Таким образом, функция u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.

Разложение (1.12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующим значениям входного сигнала.

С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянными или меняющимися уровнями. Обозначив через u 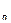(t) функцию, равную u(k t) в точках t = k t и нулю в остальных точках, запишем:

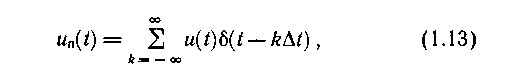
где Δt — период следования импульсов.

Поскольку умножение u(t) на дельта - функцию в момент времени t = k t соответствует получению отсчета этой функции, u_п(k t) может представлять результат равномерной дискретизации функции u(t).

§ 1.4. ЧАСТОТНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ СИГНАЛА

Рассмотрим, какие функции целесообразно выбирать в качестве базисных при анализе инвариантных во времени линейных систем. При исследовании таких систем решения всегда содержат комплексные экспоненциальные функции времени. Детерминированные сигналы, описываемые экспоненциальными функциями времени, при прохождении через инвариантные во времени линейные системы не изменяются по своему характеру, что является следствием инвариантности класса экспоненциальных функций относительно операций дифференцирования и интегрирования.

Широко используются представления детерминированных сигналов с применением базисных функций е^pt как при ρ = 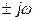(преобразование Фурье), так и при p = s+jw (обобщенное преобразование Фурье, известное как преобразование Лапласа).

До сих пор мы не касались физической интерпретации базисных функций. Для чисто математических преобразований она не обязательна. Однако такая интерпретация имеет безусловные преимущества, так как позволяет глубже вникнуть в физический смысл явлений, протекающих в системах при прохождении сигналов.

Использование экспоненциальных базисных функций в преобразовании Фурье комплексно-сопряженными парами (с положительным и отрицательным параметром ω) позволяет в соответствии с формулой Эйлера:

представить сложный детерминированный сигнал в виде суммы гармонических составляющих. Поскольку параметр ω в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.

В силу указанных преимуществ разложение сигналов по системе гармонических базисных функций подверглось всестороннему исследованию, на основе которого была создана широко известная классическая спектральная теория сигналов.

В дальнейшем, если это не оговорено специально, спектральное представление сигналов рассматривается в рамках классической теории.

Спектры периодических сигналов. Периодических сигналов, естественно, не существует, так как любой реальный сигнал имеет начало и конец. Однако при анализе сигналов в установившемся режиме можно исходить из предположения, что они существуют бесконечно долго и принять в качестве математической модели таких сигналов периодическую функцию времени. Далее рассматривается представление таких функций, как в виде суммы экспоненциальных составляющих, так и с преобразованием их в гармонические.

Пусть функция u(t), заданная в интервале времени 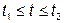и удовлетворяющая условиям Дирихле, повторяется с периодом T = 2 / 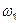= t₂-t₁ на протяжении времени от - до + .

Условия Дирихле: на любом конечном интервале функция должна быть непрерывной или иметь конечное число точек разрыва первого рода, а также конечное число экстремальных точек. В точках разрыва функцию u(t) следует считать равной.

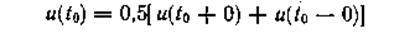
Если в качестве базисных выбраны экспоненциальные функции, то выражение (1.5) запишем в виде

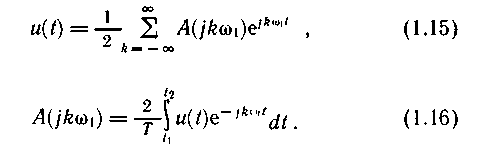
Соотношение (1.15) представляет собой ряд Фурье в комплексной форме, содержащий экспоненциальные функции как с положительным, так и с отрицательным параметром ω (двустороннее частотное представление). Составляющие с отрицательными частотами являются следствием комплексной формы записи вещественной функции.

Функцию A(jkw₁) принято называть комплексным спектром периодического сигнала u(t). Этот спектр дискретный, так как функция A(jkw₁) определена на числовой оси только для целых значений k. Значение функции A(jkw₁) при конкретном k называют комплексной амплитудой.

Огибающая комплексного спектра A(jw) имеет вид

Запишем комплексный спектр в форме

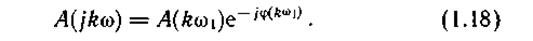
Модуль комплексного спектра A(kw₁) называют спектром амплитуд, а функцию φ(kw₁) — спектром фаз.

Если известны спектр амплитуд и спектр фаз сигнала, то в соответствии с (1.15) он восстанавливается однозначно. В практических приложениях более значимым является спектр амплитуд, а информация о фазах составляющих часто несущественна.

Поскольку A(kw₁) и φ(kw₁) отличны от нуля только при целых k, спектры амплитуд и фаз периодического сигнала являются дискретными.

Воспользовавшись формулой Эйлера е ^-jkwt = coskwt - j sinkwt, выразим комплексный спектр A(jkw₁) в виде действительной и мнимой частей:

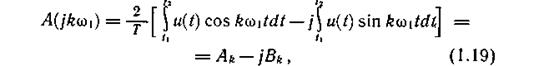
где

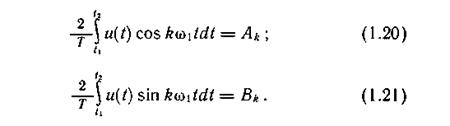
Спектр амплитуд

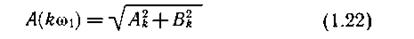
является четной функцией k, т.е.

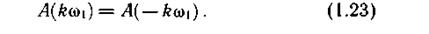
Поскольку четность A_k и В_k, противоположна, спектр фаз

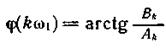
функция нечетная, т. е.

При k = 0 получаем постоянную составляющую

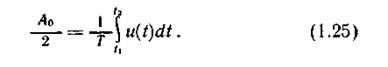
От двустороннего спектрального представления легко перейти к одностороннему (не имеющему отрицательных частот), объединяя комплексно-сопряженные составляющие [см. (1.14)]. В этом случае получаем ряд Фурье в тригонометрической форме. Действительно, выделив в (1.15) постоянную составляющую A₀/2 и суммируя составляющие симметричных частот ω и -ω, имеем

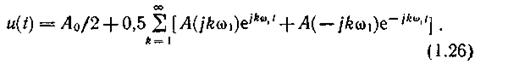
Учитывая соотношения (1.15) и (1.16), запишем

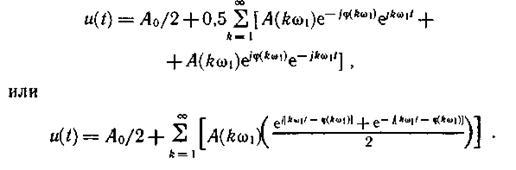
Воспользовавшись формулой Эйлера (1.14) и обозначив φ(kw₁) через φ_k, окончательно получим

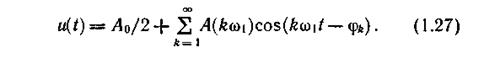
Распространена и другая тригонометрическая форма ряда Фурье, имеющая вид

Однако она менее удобна для практического применения. Отдельные составляющие в представлениях (1.23) и (1.24) называют гармониками. Как спектр амплитуд, так и спектр фаз периодического сигнала удобно представлять наглядно спектральными диаграммами. На диаграмме спектра амплитуд каждой гармонике ставится в соответствие вертикальный отрезок, длина которого пропорциональна амплитуде, а расположение на оси абсцисс отвечает частоте этой составляющей. Аналогично на диаграмме спектра фаз обозначают значения фаз гармоник. Поскольку в результате спектры отображаются совокупностями линий, их часто называют линейчатыми.

Отметим, что дискретный (линейчатый) спектр не обязательно должен принадлежать периодическому сигналу. Спектр периодического сигнала характеризует совокупность гармоник, кратных основной частоте ωι. Линейчатые спектры, включающие гармоники некратных частот, принадлежат так называемым почти периодическим сигналам. Диаграмма спектра амплитуд периодического сигнала показана на рис. 1.4. Огибающую A(t) этого спектра амплитуд можно получить, заменив kw₁ в A(kw₁) на ω, где ω = kω₁ для k-й гармоники.

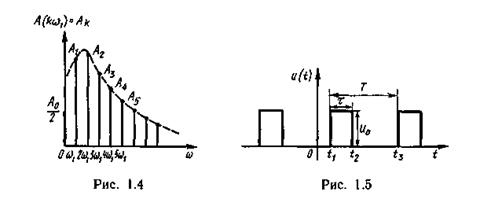
Пример 1.1. Определить спектры амплитуд и фаз периодической последовательности прямоугольных импульсов длительностью τ и амплитудой u₀, следующих с частотой ω₁ = 2π/Τ (рис. 1.5).

Функция u(t), описывающая такую последовательность импульсов на периоде, может быть задана в виде:

В соответствии с (1.16) имеем

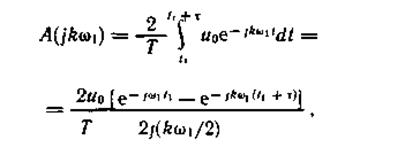
или

Амплитуды гармоник, включая постоянную составляющую, равную А₀/2, определим из выражения

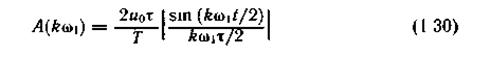
при k = О, 1, 2,....

Выбор начала отсчета времени на их величину не влияет. Огибающая спектра амплитуд определяется видом функции

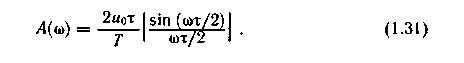
При ω = 0 получаем

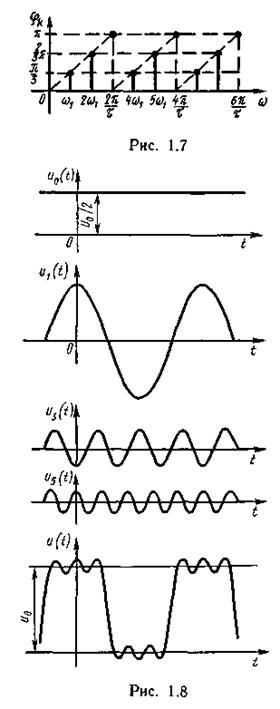Характер изменения амплитуд диктуется функцией sin х/х и не зависит от частоты следования импульсов. На частотах, кратных 2π/τ, огибающая спектра равна нулю.

На рис. 1.6 приведена диаграмма спектра амплитуд для случая

Τ/τ = 3[ω₁ = 2π/(3τ)]. Число составляющих в спектре бесконечно велико. Крутизна фронтов импульсов обусловлена наличием в спектре составляющих с частотами, существенно превышающими основную частоту ω₁.

Опираясь на формулу (1.29) и принимая во внимание, что знаки функции sin(kw₁ /2) на последовательности интервалов частот Δω = 2π/τ чередуются, выражение для спектра фаз запишем следующим образом:

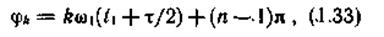
где n — номер интервала частот ω = 2π/τ, отсчитываемого от ω = 0.

Спектр фаз зависит от выбора начала отсчета. Если передний фронт прямоугольного импульса последовательности приходится на начало отсчета времени, то на каждом интервале Δω = 2π/τ фазы составляющих возрастают линейно. Диаграмма спектра фаз последовательности прямоугольных импульсов для этого случая (Τ/τ = 3, t₁ = 0) показана на рис. 1.7.

Пример 1.2. Вычислить несколько первых членов ряда Фурье для периодической последовательности прямоугольных импульсов и проследить, как их гумма сходится к указанному сигналу.

Воспользуемся результатами предыдущего примера для случая широко используемой на практике периодической последовательности импульсов, у которых длительность τ равна половине периода Т. Примем также t₁ = 0.

Поиск по сайту: