 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
АСИНХРОННИЙ ТАХОГЕНЕРАТОР З НЕМАГНІТНИМ ПОРОЖНИСТИМ РОТОРОМ
РОЗРАХУНКОВА РОБОТА №2
1. ЗАВДАННЯ
1.1. Для асинхронного тахогенератора (АТГ) нарисувати принципову схему вмикання обмоток, вказати їх напруги, ЕРС, струм, потоки. Пояснити, чому ротор використовується з немагнітного матеріалу. Нарисувати заступні схеми опорів обмоток статора для струмів симетричних складових прямої і зворотної послідовностей. Вказати, якими опорами цих схем можна знехтувати.
1.2. За наведеними в табл.1 параметри АТГ розрахувати і побудувати його ідеальні амплітудні і фазові вихідні характеристики при
· неробочому режимі (опір навантаження Zн= ∞);
· активному опорі навантаження Zн= Rн;
· індуктивному опорі навантаження Zн= jxLн;
· ємнісному опорі навантаження Zн= -jxсн;
Модуль навантаження вибрати таким, щоб забезпечити максимальну віддачу вихідної потужності тахогенератора (ТГ).
Для перелічених чотирьох характерів навантаження обчислити чутливість АТГ.
1.3. Для цих же навантажень, що у п.1.2., обчислити і побудувати залежності розрахункових амплітудних і фазових похибок реального АТГ від частоти обертання. Для одного з перелічених характерів навантаження визначити в першому наближенні експериментальні амплітудні і фазові похибки та порівняти їх із розрахунковими.
1.4. Порівняти основні показники роботи і характеристики АТГ з відповідними показниками і характеристиками ТГ інших типів.
2. Методичні вказівки до виконання завдання
До п.1.2. Вхідна напруга АТГ ÚВ визначається згідно з методом симетричних складових [4]
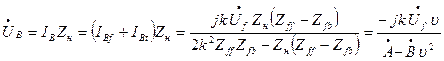 , (1)
, (1)
де
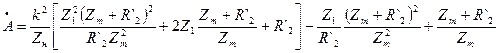 ;
;
Завдання до розрахункової роботи
| Параметри АТГ | Знач. Пара-метр. | Варіанти | |||||||||
| Напруга збудження Uf | В | ||||||||||
| Частота напруги збудження f | Гц | ||||||||||
| Номінальна частота обертання nн | об/хв | ||||||||||
| Кількість пар полюсів р | |||||||||||
| Активний опір обм. збудження Rf | Ом | ||||||||||
| Індуктивний опір обм. Збудження xδf | Ом | 3,5 | |||||||||
| Індукт. опір взаємоіндукц. між обм. збудження і обмоткою ротора xmf | Ом | ||||||||||
| Активний опір вихідн.обмот. RB | Ом | ||||||||||
| Індукт. опір взаємоіндукції між вихідною обм. І обмоткою ротора xB | Ом | ||||||||||
| Коеф-т трансформації між обм. статора K | 2,3 | 2,3 | 0,77 | 2,4 | 1,1 | 1,73 | |||||
| Табл. значення еквівал. активного опору ротора, зведеного до обм. збудження R2f | Ом |
Примітка: 1. Розрахунок значення еквівалентного опору ротора, зведеного до обмотки збудження R2` - kR2 R2f`, де kR2 – 0,8; 1,0; 1,2; 1,4; - поваріантний коефіцієнт опору ротора, який задається додатково викладачем.
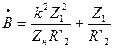 ;
; 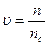 ;
; 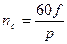 ;
;
Zff, Zfb, Z1, Zm, R`2 – опори заступної схеми обмотки збудження для струмів прямої і зворотної послідовностей.
Тут параметри заступної схеми вихідної обмотки вважаються зведеними за кількістю витків до обмотки збудження Z`B= ZB/k2= Zf і дорівнюють відповідним параметрам обмотки збудження. Але, насправді, між ними можливі невеликі розходження (RB/k2- Rf) та (xδB/k2-xδf) за рахунок різних густин струмів обмоток, кількості витків і магнітних провідностей розсіювання при розташуванні обмоток на різних статорах. Щоб симетровані обмотки вважати однаковими, ці розходження відносять до зведеного опору навантаження Z`н= Zн/k, або якщо розходження невеликі, ними нехтують (див. рис.1).
Вираз (1) використовують для обчислення вихідної напруги і похибок за допомогою ЕОМ. Якщо розрахунки проводяться вручну, то звичайно параметри генератора виражають в частках активного опору ротора R`2: ρR = R`2/R`2= 1,0; ξm= xmf/ R`2; ξs= xδf/ R`2; ρs= Rf/ R`2; γs= ρs+ jξs; γн= Z`н/ R`2. І тоді розрахунковий вираз для вихідної напруги АТГ отримуємо у вигляді [5].
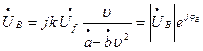 , (1а)
, (1а)
де
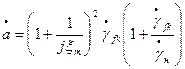 ;
; 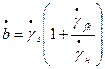 ;
;
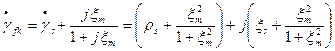 ;
;
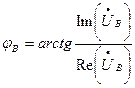 .
.
Модуль навантаження γн, яке забезпечує максимум повної вихідної потужності SB тахогенератора
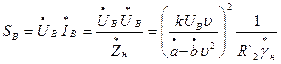
визначається з умов екстремуму функції SB(γн) і, як показано в [5, стор. 357-360], незалежно від характеру навантаження γн обчислюється у в.о.
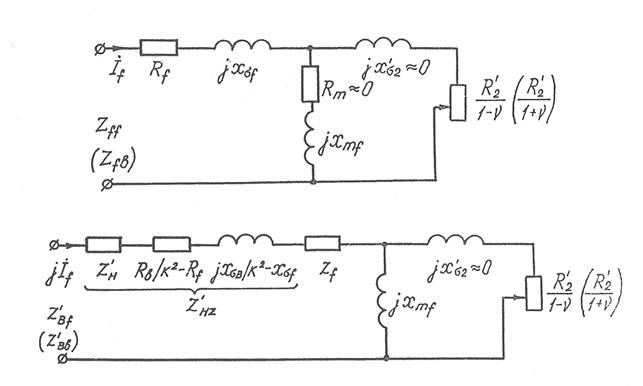
Рис.1. Заступні схеми опорів обмотки збудження і зведеної вихідної обмотки струмами прямої і зворотної послідовностей.
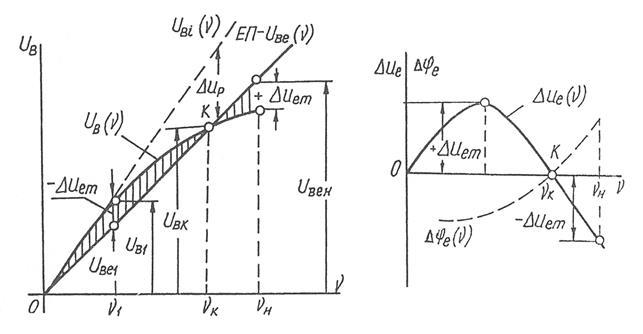
Рис.2. Амплітудні вихідні характеристики та похибки АТГ.
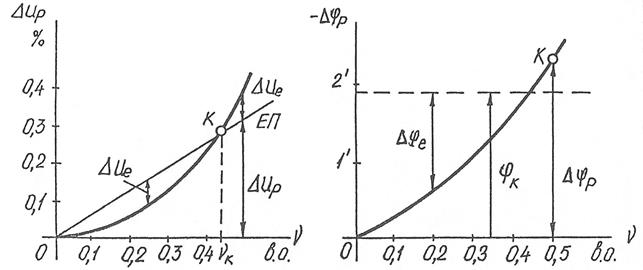
Рис.3. Експерементальні похибки АТГ
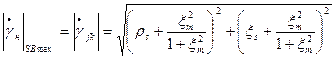 , в.о. (2)
, в.о. (2)
В іменованих одиницях цей незведений модуль опору навантаження
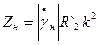 , Ом. (2а)
, Ом. (2а)
Якщо в (1) чи (1а) прийняти Ḃ=0 чи ḃ=0, отримуємо вираз для вихідної напруги ідеального АТГ, відповідно
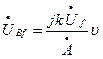 ; (3)
; (3)
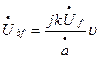 ; (3а)
; (3а)
Залежність модуля (амплітуди) Ủb та фази φВ вихідної напруги від частоти обертання тахогенератора υ при Uf = const називають, відповідно, амплітудною та фазовою вихідними характеристиками. Для ідеального АТГ амплітудна вихідна характеристика, як видно з (3) і (1) є прямою, яка проходить через початок координат і тому може бути побудована згідно (3) за двома точками
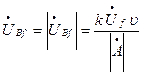 ; (4)
; (4)
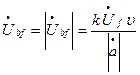 . (4а)
. (4а)
Величина фази вихідної напруги ідеального АТГ
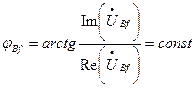 . (5)
. (5)
Чутливість тахогенератора або крутість його амплітудної вихідної характеристики в початковій її частині визначається
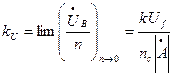 ; (6)
; (6)
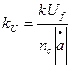 . (6а)
. (6а)
До п.1.3. За методикою [4] амплітудна і фазова розрахункові похибки АТГ обчисляються згідно з (1)
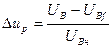 , [в.о.], де
, [в.о.], де 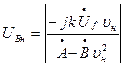 ; (7)
; (7)
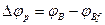 (7а)
(7а)
За методикою [5] комплексна розрахункова похибка визначається згідно з (1а) і (3а)
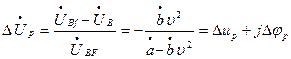 ,
,
де
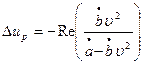 ; (8)
; (8)
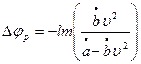 . (8а)
. (8а)
Розрахункові похибки обчислюються або за методикою [4], згідно з (7), (7а), або за методикою [5], згідно з (8), (8а) для кількох значень частоти обертання ротора, наприклад, υ= 0,25υн; 0,5υн; 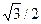 υн; υн. Після цього будують графіки Δup(υ) та Δφp(υ).
υн; υн. Після цього будують графіки Δup(υ) та Δφp(υ).
Крім розрахункових похибок, оцінюють точність ТГ при проектуванні, в процесі експлуатації широко користуються експериментальними похибками. Для визначення експериментальної амплітудної похибки на графіку дослідної амплітудної характеристики (рис.2) проводять еталонну пряму ЕП так, щоб максимальні відхилення характеристики від прямої при частотах υ1 та υн були рівними
Еталонну пряму приймають за вихідну характеристику уявного ідеального ТГ, по відношенню до якої визначаються експериментальні амплітудні похибки
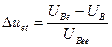 ,
,
де
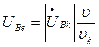 ;
; 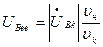 .
.
Експериментальні фазні похибки обчислюють по відношенню до фази напруги в калібровочній точці
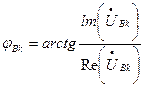 ;
;
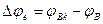 .
.
Графіки залежностей похибок Δue(υ) та Δφe(υ) показані на рис.3.
Як видно з рис.2, експериментальні похибки можна визначити з графіків розрахункових похибок (рис.4). Для цього на цих характеристиках при υk показують калібровочні точки k і через них проводять еталонні прямі ЕП для амплітудної і фазової залежностей (див.рис.4). Різниця ординат реальних характеристик і еталонних прямих наближено визначає експериментальні похибки.
Поиск по сайту: