Многокритериальность систем и решаемых задач их анализа или синтеза

Почему для исследования технических систем применяются ступенчатый входной сигнал.

Для характеристики поведения ЛСОН-систем в переходных режимах и сопоставительного анализа однотипных систем по этому признаку чаще всего используют их реакции на типовые сигналы при типовых начальных условиях. При этом за типовые начальные условия, как правило, принимают нулевые начальные условия (ННУ), определение которых применительно к обыкновенным динамическим системам было дано уже в главе 6. А в качестве типовых входных сигналов принимают ступенчатый сигнал единичного уровня 1(t) и импульсный сигнал, соответствующий функции Дирака δ (t). Их выбор в качеств типовых обусловливается тем, что если система удовлетворительно (в плане поведения в переходных режимах) реагирует на такие резко изменяющиеся входные сигналы, то она будет успешно реагировать и на входные сигналы с другими более плавными изменениями во времени.

2 вопрос:

Дискретной случайной величиной принято называть такую

случайную величину, которая может принимать значения только из

соответствующего ей фиксированного множества значений. К таким

случайным величинам относятся, например, число пассажиров в лифте

или в вагоне метро, число изготовленных цехом за смену изделий,

количество поступивших за год (месяц, день) в авторемонтную

мастерскую автомобилей.

3 вопрос:

Случайную величину, возможные значения которой образуют

непрерывное множество, принято называть непрерывной случайной

Величиной.

Напряжение в электрической сети также может изменяться случай-

ным образом и принимать любое из значений в интервале от U1 до U2.

Аналогичным образом могут меняться температура окружающей сис-

тему среды, влажность воздуха, атмосферное давление и многие другие

физические переменные, характеризующие воздействия внешней среды

на систему.

4 вопрос:

Исследование систем со случайными воздействиями на них внеш-

ней среды или же со случайным образом происходящими изменениями

самих систем обычно проводят, используя один из следующих

подходов.

1. Каждое из внешних случайных воздействий на систему прини-

мают равным «наихудшему» возможному при этом значению. Анало-

гично выбирают «наихудшие» значения параметров системы, которые

могут быть при их случайных изменениях. При таких допущениях

исследуют состояния, свойства и/или процессы такой системы. Оче-

видно, базирующиеся на таких исходных предпосылках исследования

будут давать далеко не адекватные реальным результаты, так как

подобные совпадения в реальных условиях работы системы мало-

вероятны. Если подобные исследования проводятся с целью создания

системы, то в итоге проектируемая система окажется, скорее всего,

малоэффективной. Например, если исследование точности проектируе-

мой системы автоматической стабилизации электрического напряжения

в сети вести, приняв максимальное значение случайного возмущения

(нагрузки), то в этом случае система окажется рассчитанной с чрез-

мерным запасом.

2. Расчет системы проводят, базируясь на статистической природе

ее случайных возмущений и состояний, т. е. с учетом их статистических

характеристик. В таких случаях состояния, свойства, характеристики

системы и протекающие в ней процессы определяются как ожидаемые

усредненные (статистические).

Математической основой такого метода анализа систем являются

теория вероятностей и теория случайных функций.

5 вопрос:

Функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.

6 вопрос:

Функция - производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины.

Термины «плотность распределения», «плотность вероятности» становятся особенно наглядными при пользовании механической интерпретацией распределения; в этой интерпретации функция буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»). Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.

7 вопрос:

Каждая случайная величина полностью определяется своей функцией распределения.

В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.

8 вопрос:

Математическое ожидание, среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины. Для случайной величины X, принимающей последовательность значений y1, y2,..., yk,... с вероятностями, равными соответственно p1, p2,..., pk, …, М. о. определяется формулой

Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины.

Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.

Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия случайной величины (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина.

Дисперсия случайной величины имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью случайной величины.

Средним квадратическим отклонением случайной величины Х называется корень квадратный из ее дисперсии:

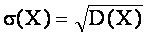
9 вопрос:

Если аргументом случайной функции является время, то такая

функция называется также стохастической функцией, а описываемый

ею процесс – стохастическим процессом

Стохастические процессы характеризуются тем, что знание их на некотором интервале времени позволяет определить лишь вероятностные характеристики поведения этих процессов вне этого интервала.

Если эти вероятностные характеристики, например плотности распределения, заранее заданы, то и в этом случае можно определить в явной форме критерий оптимальности и ограничения, которые представляют собой, как это упоминалось выше, некоторые условные математические ожидания.

10 вопрос:

Случайный процесс (СП) это некоторый процесс или явление, поведение которого в течение времени и результат заранее предсказывать невозможно. Примеры случайных процессов: динамика изменения курса валют или акций, выручка или прибыль организации с течением времени, объемы продаж товара и т.д.

Если случайный процесс может изменить своё состояние только в строго определённый момент времени, то он называется процессом с дискретным временем.

Если же смена состояния возможна в произвольный момент времени, то это СП с непрерывным временем.

Если в любой момент времени СП представляет собой дискретную случайную величину (ее значение можно перечислить и выделить два соседних значения), то это процесс с дискретным состоянием.

Если же в любой момент времени состояние может меняться непрерывно, плавно и нельзя выделить два соседних состояния, то это СП с непрерывным состоянием.

Таким образом, возможно 4 вида СП:

1) СП с непрерывным временем и непрерывным состоянием (пример: температура воздуха в некоторый момент времени, изменяется плавно в любой момент времени).

2) СП с непрерывным временем и дискретным состоянием (пример: число посетителей в магазине, изменяется кратно одному в любой момент времени).

3) СП с дискретным временем и непрерывным состоянием (пример: динамика курса курс валюты, изменяется плавно в момент валютных торгов).

4) СП с дискретным временем и дискретным состоянием (пример: число пассажиров в транспорте изменяется кратно одному и только в определенные моменты времени, на остановках).

11 вопрос:

Чисто случайные процессы. В этом случае все значения описывающей такой процесс случайной функции x x(t) в отдельные моменты

времени не зависят друг от друга. В этих процессах значения (),

()……, (), и т. д. будут независимыми событиями. В связи с

этим вероятность их совместного наступления, как известно из теории

вероятностей, равна произведению вероятностей наступления каждого

из них в отдельности, и поэтому

W(; ;…….., )=W()×W()×……× (),

Математическое описание чисто случайных процессов является

наиболее простым и используется при анализе систем автоматизации и

управления чаще всего для характеристики некоторых видов шумов.

12 вопрос:

Марковские процессы. К ним относят такие процессы, дальнейший ход которых в любой момент времени обусловливается только их

состояниями в этот момент и не зависит от характера течения процесса

в предшествующий период.

Примером такого процесса можно считать движение в лабиринте,

если рассматривать его как совокупность последовательной реализации

возможных альтернативных выборов в каждом из встречающихся пере-

крестков или разветвлений. Подобные процессы являются типичными

для так называемых «конечных автоматов.

13 вопрос:

Коррелированные процессы. Во многих технических системах

ход процесса (x,t), начиная с любого промежуточного момента време-

ни, зависит в той или иной степени от значений (x,t) в предыдущие

моменты времени, т. е. как он протекал до этого.

Так, например, координаты положения летательного объекта (само-

лёта, ракеты), определяемые с помощью радиолокатора, случайны. Тем

не менее, объект не может в силу инерционности как угодно быстро

менять свою скорость и координаты. Поэтому если он занимал поло-

жение x 1 в момент t 1, то его положение x 2 в момент t 2 уже ограни-

чено, и, следовательно, события () и ( не являются незави-

симыми. Значит, взаимозависимыми будут и координаты объекта, опре-

деляемые радиолокатором. Чем более инерционен объект, тем больше

эта взаимосвязь, или корреляция.

Вопрос 14

Математическая модель системы – это уравнения, неравенства или другие матиматические образы, позволяющие проводить количественный анализ хотя бы одного из свойств, характеристик системы или её структуры, состояний взаимодействий с внешней средой или без токого.

Вопрос 15.

Математическое моделирование системы представляет собой процесс формирования из математических символов математических уравнений, а в ряде случаев и неравенств или других математических образов, отражающих с приемлемой точностью структуры, свойства, характеристики, состояние этих систем, их связи с внешней средой и/или протекающие в них процессы.

Вопрос 16.

Вся совокупность интересующих разработчиков свойств и характеристик систем состоит из двух групп:

1) Внутренние свойства и характеристики систем

2) Свойства и характеристики систем, проявляющиеся при их взаимодействие с внешней средой (внешние свойства и характеристики систем)

Вопрос 17.

Сложности математического описания свойств и состояний систем.

1.Сложность самой описываемой системы. Обычно возникают проблемы выбора типа математической модели.

2. Недостаток сведений о принципах работы либо о взаимосвязях величин, характеризующих свойства и состояния отдельных элементов или системы в целом.

3. Необходимость описания свойств и состояний нетолько в фиксированные моменты времени но и в динамической системе.

4. Неявно выраженная зависимость точности описания изучаемых по формируемой математической модели свойств, характеристик или состояний от выбираемого типа модели и её параметризации.

5. Невозможность априорной оценки влияния того или иного свойства отдельных элементов систем.

6. Невозможность оценить точностные свойства формируемых и используемых математических моделей для многих создаваемых новых систем до изготовления и экспериментального исследования последних.

7. Сложность количественной оценки важных для многих систем свойств из-за отсутствия предложенных для этого количественных показателей и способов их определения.

Вопрос 18.

Основные разделы кибернетики.

- Техническая кибернетика, ориентированную на разработку и исследования на основе единых для кибернетики методов технических систем управления.

- Теорию информации, занимающуюся математическим описанием и оценкой методов и средств формирования, передачи, хранения, извлечения и классификации информации.

- Системотехнику, ориентированную на исследования и проектирования сложных систем различной физической природы на основе концепции и методов системного анализа.

-Теорию автоматов, изучающую математические модели (называемые автоматами) реально существующих технических и других устройств и систем, перерабатывающих дискретную информацию дискретными временными тактами.

Вопрос 19.

Понятие «системы» в кибернетике:

Понятие отражает отличие системного объекта от несистемного и укзывает на то, как строить систему или выделять её из окружающей среды, отображать её целевое назначение.

Вопрос 20

Дескрипторное определение систем

-система-это совокупность элементов, находящихся в отношениях и связях друг с другом, которая образует определённую целостность, единство.

-система- это совокупность объектов, свойство которой определяются отношением между этими объектами;

Вопрос 21

Конструктивное определение системы базируется на функционально – целевом подходе и подсказывают, какова стратегия формирования системы. При этом подразумевается, что окружающий систему мир тоже есть бесконечное множество объектов, систем находящихся в определённых отношениях между собой.

Вопрос 22

Классификация систем в кибернетики

1) по форме существования делятся на физические и абстрактные.

2) по способу создания различают системы искусственного и естественного происхождения.

3) По природе входящих в системы элементов выделяют технические, биологические, социальные, экономические, энергетические.

4) По целевой ориентации выделяют системы целеноправленного типа и без явно выраженной цели.

5) По целевому назначению системы делят на системы предназначенные для достижения одной, двух, трех, и более целей.

6) По характеру своего развития системы делят на элементно- и функционально стабильные и развивающиеся.

7) По характеру взаимосвязи с внешней средой выделяют системы открытые и закрытые.

8) По приспосабливаемости к условиям существования делятся на неприспосабливающиеся и приспосабливающиеся.

9) По количественному признаку все компоненты систем могут рассматриваться как монокомпонентные и поликомпонентные.

10) По структуре связи между элементами различают системы с последовательными связями, с параллельными, с обратными, с с кольцевыми, со звёздными.

11) По степени сосредоточенности в пространстве различают сосредоточенные и распределённые.

12) По положению относительно внешней среды делят на подвижные и неподвижные.

Вопрос 23

Свойства «сложной» системы

1)многомерность(большая размерность,большое число элементов)

2)многообразие элементов системы (различают по назначению и по физической природе)

3)многообразие возможных форм связей между элементами и разнородность используемых в ней структур(иеархических, с последовательными и параллельными включениями)

4)многокретиальность наличиенескольких часто противоречивых критериев которым должна удовлетворять система.

5)многократные изменения состава или структуры системы в процессе фунционирования.

6)многоплановость при моделирование и исследование её свойств.

Вопрос 24

Принцип системного подхода

1 )целостность под ней понимают принципиальную несводимость свойств системы к простой сумме свойств составляющих её элементов.

2) взаимозависимость системы и среды, согласно которой система формирует и проявляет свои свойства.

3) целенаправленность как самой системы, так и решаемых задач анализа или синтеза.

4) структурность возможность описания системы с использованием информации об её структуре, связях и отношениях элементов в системе.

5) обусловленность поведения системы не только свойствами и поведением её элементов, но и свойствами её структре

6) многоуровневость отражающая тот факт, что часть или даже все элементы системы в свою очередь, тоже могут рассматриваться как системы.

7) множественность описания

8) причинность, подчёркивающая причинно-следственный характер свойств протекающих в

системе процессов.

9) непротиворечивость целей, отражающая тот факт недопустимости преволирования целей отдельных элементов над общей целью все системы.

10) многовариантность достижения поставленных целей

многокритериальность систем и решаемых задач их анализа или синтеза

12) ограниченность ресурсов, нацеливающая на учёт ограничения, которая имеет сама система по входам и внутреннем ресурсам.

Вопрос

По целевому назначению различают математические модели,

используемые для описания структур, функций, свойств, характеристик,

состояний и процессов в системах и их элементах. При этом часть из

них может одновременно отражать и некоторые совокупности из пере-

численных выше описаний систем. В частности, одна и та же ММ

может одновременно служить для описания состояний и протекающих в

системе процессов, а также для определения ряда её свойств.

2. По уровню проектирования, на котором используется та или

иная модель, последние делят на модели, предназначенные для струк-

турного, функционального, логического, схемотехнического, конструк-

торского и поэлементного проектирования

3. По форме представления математические модели могут быть

аналитическими, матричными, табличными, графовыми, операторно-

структурными или алгоритмическими.

4. По типам используемых величин различают математические

модели, включающие в себя переменные и константы, определённые на

поле действительных (вещественных) чисел R, натуральных чисел N,

целых чисел Z, комплексных чисел С, либо переменные, определён-

ные на элементах B   0,1  булевой или какой-либо другой многознач-

ной (бесконечнозначной) логики L [7].

5. По отражаемой обусловленности от времени описываемых

свойств, состояний и характеристик систем различают модели ста-

тические и динамические.

6. По характеру обусловленности параметров математиче-

ской модели от времени различают модели стационарные и неста-

ционарные. В первых моделях (и описываемых ими системах) все пара-

метры не зависят от времени, а во вторых – хотя бы один из параметров

меняется во времени.

7. По способу отсчёта времени динамические ММ делят на

модели с непрерывным временем (с непрерывным аргументом) и

модели с дискретным временем.

8. По отсутствию или наличию смещённых аргументов у

входящих в модель переменных различают системы с несмещённым

аргументом (временем t) и системы со смещённым аргументом.

9. По причине изменения переменных, характеризующих описы-

ваемую систему, математические модели делят на модели с времен-