АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение типовой задачи. Задача. Исследовать функцию на экстремум и определить интервалы её возрастания и убывания

Читайте также:
  1. I. Прокурор: понятие, положение, функции и профессиональные задачи.
  2. I. СУЩНОСТЬ, ЦЕЛЬ И ЗАДАЧИ КУРСОВОЙ РАБОТЫ
  3. I. ЦЕЛИ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
  4. II. Задачи территориального фонда
  5. II. ОСНОВНЫЕ ЦЕЛИ И ЗАДАЧИ КОНЦЕПЦИИ
  6. II. Основные цели и задачи Программы, срок и этапы ее реализации, целевые индикаторы и показатели
  7. II. Цели и задачи Конкурса
  8. II. ЦЕЛИ И ЗАДАЧИ КУРСА
  9. III. Задачи Фестиваля
  10. IV. Решите задачи.
  11. IV. Решите задачи.
  12. PR - public relations (общественные связи): цели и задачи, области их использования, инструменты PR.

Задача. Исследовать функцию на экстремум и определить интервалы её возрастания и убывания. Найти точки перегиба графика этой функции и определить интервалы его выпуклости и вогнутости. Построить график данной функции.

 

Решение. Исследуем данную функцию на экстремум с помощью производной. Определим критические точки. Для этого находим первую производную данной функции и приравниваем её к нулю:

Решая последнее уравнение, находим его корни и Таким образом, и — критические значения аргумента. Так как производная существует при любом значении , то других критических точек не имеется.

Исследуем критическую точку . Определим знак первой производной левее и правее этой точки в достаточно малой её окрестности. Производную можно представить в виде произведения двух сомножителей:

. (*)

Из равенства (*) видно, что при производная положительная, а при производная отрицательна. Следовательно, в интервале функция возрастает, а в интервале - убывает. Так как производная при переходе через критическую точку меняет свой знак с плюса на минус, то в этой точке функция имеет максимум.

Теперь исследуем критическую точку 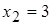. Из равенства (*) видно, что при 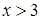производная положительна. Следовательно, в интервале функция возрастает. Так как производная при переходе через критическую точку 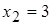меняет свой знак с минуса на плюс, то в этой точке функция имеет минимум.

Вычислим значение функции в точках экстремума:

точки максимума 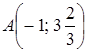и минимума отмечены на рисунке, где показан график исследуемой функции.

Определим точки перегиба графика функции и интервалы выпуклости и вогнутости. Для этого находим вторую производную , приравниваем её к нулю и находим действительные корни уравнения :

.

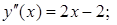
Отсюда критическая точка второго рода. Запишем вторую производную в виде:

. (**)

Из правой части равенства (**) следует, что при 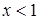вторая производная отрицательна, а при положительна. Следовательно, в интервале график функции является выпуклым, а в интервале 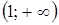— вогнутым.

Как видно, вторая производная при переходе через точку 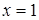меняет свой знак. Следовательно, 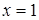есть абсцисса точки перегиба. Вычислим ординату этой точки:

.

Таким образом, – точка перегиба графика функции.

Рис. 2

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)