 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема III. Элементы интегрального исчисления
[1], гл. XІІІ, §§ 1–5; гл. XІV, §§ 1–3, 5, 9.
[2], ч. І, гл. VІІІ, § 1; гл. ІX, §§ 1–3.
[3], гл. X, §§ 1–9, 12; гл. XІІ, §§ 1, 5, 8.
[6], задачи: 1264, 1266, 1274, 1285, 1290, 1298, 1299, 1301-1306, 1625, 1635,1653, 1664.
Таблица основных неопределенных интегралов
(18) 
(19) 
и т.д.
(20) 
(21) 
(22) 
(23) 
(24) 
(25) 
(26) 
(27) 
(28) 
(29) 
(30) 
, где А — любое действительное число.
31-40. Задачи контрольной работы. Найти указанные неопределённые интегралы.
31. а) 
б) 
в) 
32. а) 
б) 
в) 
33. а) 
б) 
в) 
34. а) 
б) 
в) 
35. а) 
б) 
в) 
36. а) 
б) 
в) 
37. а) 
б) 
в) 
38. а) 
б) 
в) 
39. а) 
б) 
в) 
40. а) 
б) 
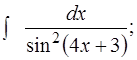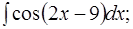в) 
Решение типовых задач
Задача. Найти неопределенные интегралы:
а) 
б) 
в) 
Решение. а) Предварительно преобразуем подынтегральную функцию и затем применим свойства неопределённого интеграла и формулу (20) Таблицы интегралов:
= 
= 
= 
б) воспользуемся подстановкой 
, тогда 
, откуда 
. Таким образом,
= 
.
При вычислении неопределённого интеграла, полученного в результате замены переменной, мы пользовались формулой (21) Таблицы интегралов.
в) В неопределённом интеграле выполним замену 
, чтобы привести его к табличному виду. Тогда 
. Получим:
При вычислении неопределённого интеграла 
была использована формула (20) Таблицы интегралов.
41-50. Задачи контрольной работы. Вычислить с помощью определённого интеграла площадь фигуры, ограниченной параболой и прямой. Сделать чертеж и заштриховать искомую фигуру.
41. 
42. 
43. 
44. 
45. 
46. 
47. 
48. 
49. 
50. 
Решение типовой задачи
Задача. Вычислить площадь фигуры, ограниченной параболой 
и прямой
Решение. Площадь фигуры, ограниченной сверху непрерывной кривой 
, снизу — непрерывной кривой 
, слева — прямой 
, справа — прямой 
, вычисляется по формуле:
. (***)
Найдем точки пересечения заданных параболы и прямой. Составим и решим систему их уравнений:
.
Подставив в первое уравнение системы вместо у сумму х + 3, получим:
, 
, 
,
, 
.
Отсюда, 
Тогда 
Таким образом, парабола и прямая пересекаются в точках 
и 
.
Из формулы (***) следует, что площадь фигуры равна
= 
= 
= 
Следовательно, искомая площадь равна 1,5 кв. ед. Рассмотренная фигура изображена на рисунке.
Рис. 3
Поиск по сайту: