Решение типовой задачи

Задача. В стаде из 70 телят заболели 3 теленка. Какова вероятность того, что наудачу взятый теленок окажется здоровым?

Решение. Пусть событие А состоит в том, что случайно выбранный теленок здоров. Случайный отбор подразумевает, что все исходы события А равновозможные. Всего исходов , исходов, благоприятствующих событию А, . Следовательно, искомая вероятность Р (А) =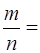

71-80. Задачи контрольной работы. Задан закон распределения случайной величины в виде таблицы; в первой строке таблицы указаны возможные значения случайной величины Х, во второй – соответствующие вероятности. Вычислить: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение.

71.

	0,2	0,1	0,3	0,3	0,1

72.

	0,1	0,1	0,6	0,1	0,1

73.

	0,2	0,3	0,2	0,1	0,2

74.

	0,1	0,3	0,4	0,1	0,1

75.

	0,2	0,3	0,3	0,1	0,1

76.

	0,1	0,2	0,4	0,2	0,1

77.

	0,1	0,1	0,3	0,3	0,2

78.

	0,2	0,2	0,3	0,2	0,1

79.

	–5	–1
	0,2	0,4	0,2	0,1	0,1

80.

	–10
	0,1	0,2	0,3	0,3	0,1

Решение типовой задачи

Задача. Задан закон распределения дискретной случайной величины Х.

	–1
	0,2	0,1	0,4	0,2	0,1

Вычислить: 1) математическое ожидание; 2) дисперсию;
3) среднее квадратическое отклонение.

Решение. 1) математическое ожидание дискретной случайной величины вычисляется по формуле:

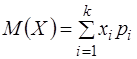
Подставляем данные задачи в формулу, получаем

= .

2) дисперсия дискретной случайной величины вычисляется по формуле:

.

Подставляем сюда данные , получаем:

+

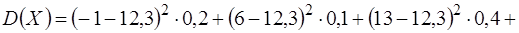
35,378+3,669+0,196+11,858+21,609=73,01.

3) среднее квадратическое отклонение находится по формуле:

Тема VI. Основы математической статистики

[5], гл. XV, §§ 1–3, 6–8; гл. XVІ, §§ 1–5, 8–10. 13–18; гл. XVІІI, §§ 1, 3, 4, 7, –3; гл. ІXX, §§ 1–4, 23.

Задача по данной теме, а также методические указания для ее решения (фактически пошаговая инструкция для ее решения) содержатся в Приложении 1.

Статистические данные для решения задачи содержатся Таблице 1A (формат.ods) и в Таблице 1B (формат.xls), данные в обеих таблицах идентичны. Вам нужно взять данные из Листа «Вариант #», где # – номер Вашего варианта.

Кроме того, в Листе "Отдельные расчеты для решения задачи" каждой из таблиц содержатся шаблоны для выполнения некоторых пунктов задачи.

Содержание

Общие методические указания...................................................................... 3

Рекомендуемая литература........................................................................... 4

Тема І. Введение в анализ.............................................................................. 4

Тема II. Дифференциальное исчисление........................................................ 6

Тема ІII. Элементы интегрального исчисления........................................... 12

Тема IV. Дифференциальные уравнения.................................................... 17

Тема V. Основы теории вероятностей......................................................... 18

Тема VI. Основы математической статистики.…...…………………………..22

Содержание ….......................................................................................................22

Поиск по сайту: