Численное интегрирование методом Симпсона

Цель работы

Исследование и реализация методов численного интегрирования.

Задание (4.6)

Составить программу, реализующую четыре метода численного интегрирования:

— метод прямоугольников;

— метод трапеций;

— метод Симпсона;

— метод Монте-Карло.

И рассчитать для указанной функции в заданных приделах с числом разбиений, равным 4, 10, 50, 500. Результат сравнить с точным значением.

Функция Пределы Точное значение

Численное интегрирование методом прямоугольников

1.1 Теоретический материал:

В методе прямоугольников промежуток интегрирования разбивается на равные отрезки, и на каждом отрезке вычисляется площадь прямоугольника, одна сторона которого - отрезок между соседними точками, а вторая - значение функции в одной из точек. Сумма площадей прямоугольников составляет площадь криволинейной трапеции, которая и является значением интеграла.

Чем больше число отрезков, тем точнее получается результат.

Формула метода прямоугольников следующая:

1.2 Блок-схема:

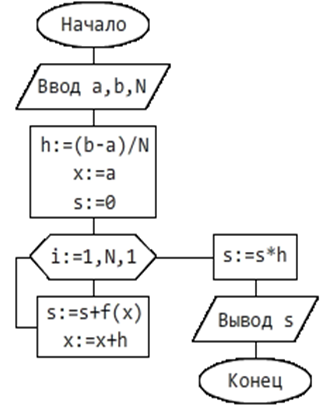
Рисунок 1 – Метод прямоугольников.

1.3 Результат работы:

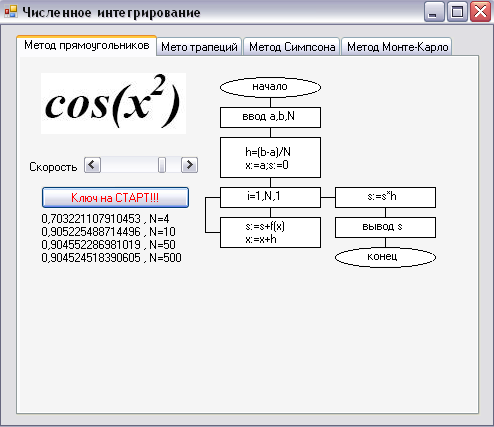
Рисунок 2 – Результат вычисления методом прямоугольников.

Численное интегрирование методом трапеций

2.1 Теоретический материал:

В методе трапеций вместо площадей прямоугольников вычисляются площади трапеций, на которые разбивается фигура под кривой. Это даёт более точные результаты.

Формула метода трапеций следующая:

2.2 Блок-схема:

Рисунок 3 – Метод трапеций.

2.3 Результат работы:

Рисунок 4 – Результат вычисления методом трапеций.

Численное интегрирование методом Симпсона

3.1 Теоретический материал:

В методе Симпсона вместо прямоугольников и трапеций высчитывается площадь фигур, ограниченных параболами, что даёт ещё более точные результаты.

Формула метода Симпсона следующая:

3.2 Блок-схема:

Рисунок 5 – Метод Симпсона.

3.3 Результат работы:

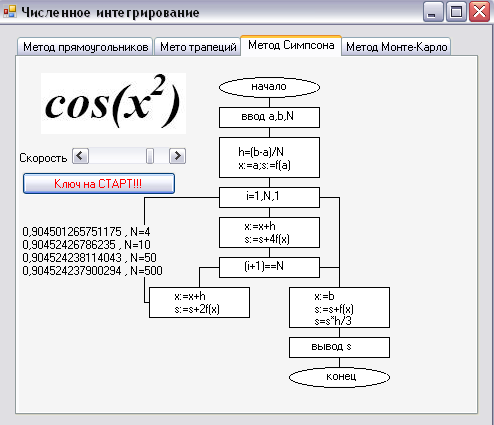
Рисунок 6 – Результат работы вычисления методом Симпсона.

Поиск по сайту: