АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Средняя арифметическая. Структурные степенные средние

Читайте также:
  1. Арифметическая середина и ее свойства.
  2. Взвешенная средняя арифметическая
  3. Вопрос 29. Средняя геометрическая и её определяющее свойство
  4. ГОРОДА НОВОСИБИРСКА «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 45» (МБОУ СОШ № 45)
  5. Деление дохода на потребление (C) и сбережения (S). Средняя и предельная склонность к потреблению (АРС, МРС) и сбережения (APS, MPS).
  6. Доход семьи составил 500 ден.ед., а потребительские расходы – 450 ден.ед. Чему равна в этом случае средняя склонность к сбережению?
  7. Иран и Средняя Азия в 1 веке.
  8. По этой формуле рассчитывается средняя квадратическая ошибка прогноза у0 с волной
  9. Потребление и сбережение, факторы их определяющие. Предельная склонность к потреблению и сбережению. Средняя склонность к потреблению и сбережению.
  10. Потребление: факторы и функция. Средняя и предельная склонность к потреблению.
  11. Производственное и непроизводственное потребление. Средняя и предельная склонности к потреблению. Функция и график потребления.
  12. Психологическая склонность к потреблению и сбережению. Средняя склонность к потреблению и сбережению. Предельная склонность к потреблению и сбережению, их взаимосвязь.

Структурные степенные средние. Показатели изменчивости вариационного ряда.

Структурные средние величины.

Медиана (Ме) эмпирического распределения – это средняя, относительно которой ряд делится на две половины, в обе стороны одинаковое число вариант.

Непрямой способ нахождения Ме: Ме=Хме+λ*

Где Хме – начало класса, в котором находится Ме

fме - частота медианного класса

S – сумма частот классов, предшествующих медианному

Мода (Мо) – величина, которая встречается в совокупности наиболее часто. Это точка на оси абсцисс, соответствующая максимальной частоте теоретической кривой распределения вариант.

Мо= Хмо+λ*

f1 – класс, предшествующий модальному

f2 – модальный класс

f3– последующий класс

Квартиль(q) – делит совокупность на 4 части

Дециль (d) – на 10

Перцентиль (p) – на 100

 

1) Степенные средние величины

_

Средняя гармоническая (Н или Хh)(устьица на березе,в среднем должно быть5 на5листьев)

 

H =

Средняя квадратическая (привыражении признаков по площади:продуктивность,активность и т.д)

Xq (s) =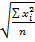

Средняя кубическая (объемная характеристика)

Xк =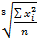

Средняя геометрическая

(g) =

Средняя взвешенная(при повторении какой-либо варианты)

=

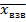Средняя арифметическая

=

 

Свойства средней арифметической:

1. Если каждую варианту совокупности уменьшить или увеличить на какое-то число А, то и среднее уменьшится или увеличится на столько-же.

Среднее, найденное для одной совокупности, не может быть механически перенесено на другую совокупность или на отдельную ее часть.

2. Если каждую варианту разделить или умножить на одно и то же А, то и ср. арифм. Изменится в такое же число раз.

3. Алгебраическая сумма отклонений отдельных вариант от ср. арифм. или сумма разностей между каждой вариантов и средней арифметической равна нулю.

4. Сумма условных отклонений или отклонений вариант от любого значения, неравная средней арифм., не равна нулю.

; (A ).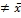

5. Сумма квадратов отклонений вариант от их средней меньше суммы квадратных отклонений тех же вариант от любой для А не равно нулю.

 

Непрямой способ нахождения средней арифметической (См пример в лекции)

 

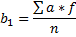
Показатели изменчивости вариационного ряда. Группы показателей:

· Меры положения(Мо и Ме и др.)

· Меры рассеивания(дисп,ст откл)

· Меры формы (асимметрия, эксцесс)

· Меры достоверности(вероятность)


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)