 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Приближение функции одной переменной
1° Постановка задачи линейной интерполяции (ЛИ)
Пусть задана функция  область определения и область значения
область определения и область значения  ,
,  функциональное пространство.
функциональное пространство.
(Примеры функциональных пространств:  пространство непрерывных на
пространство непрерывных на 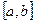 функций,
функций,  пространство непрерывно-дифференцируемых на
пространство непрерывно-дифференцируемых на 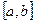 функций,
функций,  пространство непрерывных дважды дифференцируемых на
пространство непрерывных дважды дифференцируемых на 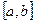 функций,
функций,  пространство интегрируемых на
пространство интегрируемых на 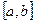 функций (лебегово пространство)).
функций (лебегово пространство)).
Постановка задачи линейной интерполяции (ЗЛИ):
Требуется построить для функции  приближающую функцию
приближающую функцию  вида:
вида:
 , (1)
, (1)
где  числа,
числа,  функции,
функции,
такую, чтобы были выполнены линейные условия интерполяции:
 ,
,  (2)
(2)
df1. Задача построения такой приближающей функции 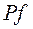 называется задачей линейной интерполяции (ЗЛИ).
называется задачей линейной интерполяции (ЗЛИ).
Примеры интерполяций.
1) Линейная интерполяция по набору многочленов
Рассмотрим функцию  .
.
Пусть  область определения
область определения
 область значений
область значений
Тогда  функциональное пространство
функциональное пространство
 набор функций, принадлежащих тому же пространству, что и функция f.
набор функций, принадлежащих тому же пространству, что и функция f.
Получим следующую приближающую функцию 
2) Поточечная интерполяция

 , где
, где  набор точек на отрезке
набор точек на отрезке 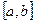 .
.
3) Интегральная интерполяция
 где
где
 набор точек на отрезке
набор точек на отрезке 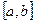 .
.
df2. Задача линейной интерполяции называется корректной, если её решение (набор чисел  ) существует и единственно для
) существует и единственно для  функции
функции  .
.
df3. Числовую функцию  , определённую на некотором пространстве
, определённую на некотором пространстве  называют функционалом, если выполнены следующие условия:
называют функционалом, если выполнены следующие условия:
1) 
2) 
Th1. Пусть функции  линейно-независимы и функционалы
линейно-независимы и функционалы  также линейно-независимы. Задача линейной интерполяции (ЗЛИ) корректна <=>(тогда и только тогда, когда)
также линейно-независимы. Задача линейной интерполяции (ЗЛИ) корректна <=>(тогда и только тогда, когда)  и матрица
и матрица

 (3)
(3)
обратима.
Пояснение:

 (Матрица
(Матрица  называется обратной к матрице
называется обратной к матрице  , если
, если  ).
).
 : Из условий линейной интерполяции (1), (2) имеем:
: Из условий линейной интерполяции (1), (2) имеем:
 <=> (тогда и только тогда, когда):
<=> (тогда и только тогда, когда):  (для
(для  ) или
) или
 (4)
(4)
Обозначим через  элементы матрицы
элементы матрицы  , через
, через  вектор-столбцы матрицы
вектор-столбцы матрицы  ,тогда вместо условия (4) получим:
,тогда вместо условия (4) получим:
 .
.
Поскольку  , то
, то
 (5)
(5)
Следовательно, ЗЛИ корректна <=> когда СЛУ имеет решение для любой функции  . Значит матрица
. Значит матрица  осуществляет биективное отображение (взаимно-однозначное соответствие) между множеством
осуществляет биективное отображение (взаимно-однозначное соответствие) между множеством  и множеством
и множеством  . Это и означает, что
. Это и означает, что  и существует обратная матрица
и существует обратная матрица  .
. 
Теорема доказана.
Поиск по сайту: