Тема: Парная линейная регрессия и корреляция. 1. Дисперсионный анализ результатов регрессии

Содержание занятия:

1. Дисперсионный анализ результатов регрессии.

2. Статистическая оценка значимости уравнения и параметров уравнения линейной регрессии.

3.Расчет относительной ошибки аппроксимации. Оценка качества построенной модели с помощью средней ошибки аппроксимации.

4.Использование статистической функции ЛИНЕЙН и программы анализ данных для определения параметров регрессии.

Литература: [1] стр48-57, [2] стр6-9, [3] стр89-114, [11] стр7-11

Задание №1 Имеются следующие исходные данные:

Провести дисперсионный анализ результатов регрессии и статистическую оценку значимости уравнения и параметров уравнения линейной регрессии.

Методические указания по выполнению задания:

F-тест – оценивание качества уравнения регрессии - состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера. F_факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: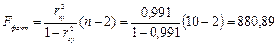

где n - число единиц по совокупности; m -число параметров при переменных х.

Табличное значение при уровне значимости 0,05 составляет 5,32.

Поскольку F_табл < F_факт, то гипотеза Н₀ отклоняется и признается статистическая значимость и надежность уравнения регрессии.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t–критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н₀ о случайной природе формирования показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной стандартной ошибки:

.

Стандартные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

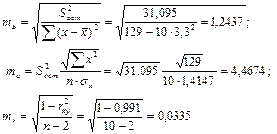
Значения t-критерия Стьюдента:

Табличное значение t-критерия Стьюдента при уровне значимости 0,05 равно 2,306. Сравним фактические значения с табличным значением: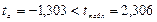

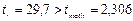
Гипотеза Н_{0 о} случайной природе формирования параметра a принимается и признается статистическая незначимость данного показателя. А параметр b и линейный коэффициент корреляции r не случайно отличаются от нуля и сформировались под влиянием действующего фактора х, гипотеза отклоняется и признается их статистическая значимость и надежность.

Для расчета доверительных интервалов определяются предельные ошибки D для каждого показателя: .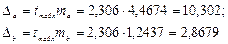

Доверительные интервалы рассчитываются следующим образом: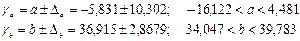

Задание №2 Имеются следующие исходные данные:

Оценить качество построенного уравнения регрессии с помощью средней ошибки аппроксимации. Определить параметров регрессии при помощи статистической функции ЛИНЕЙН и программы анализ данных.

Методические указания по выполнению задания:

По результатам расчетов, сделанных на предыдущих занятиях заполним следующую таблицу:

№	x	y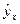
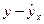
			31,09 141,84 104,92 68,01 104,92 178,76 215,67 141,84 104,92 68,01	-1,09 8,16 -4,92 1,99 -4,92 1,24 -5,67 8,16 -4,92 1,99	3,63 5,43 4,93 2,84 4,93 0,69 2,7 5,44 4,93 2,84
Итого					38,38
среднее	3,3		-	-	3,838

Рассчитаем относительные ошибки аппроксимации (6 графа), используя формулу: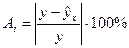

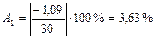
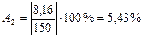и т.д.

Средняя ошибка аппроксимации составит: .

Качество построенной модели оценивается как хорошее, т. к. в среднем расчетные значения отклоняются от фактических значений на 3,83% и не превышают допустимого предела 8-10%

С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики побора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:

1) в главном меню выберите пункты Сервис/ Анализ данных/ Регрессия. Щелкните по кнопке ОК.

2) заполните диалоговое окно ввода данных и параметров вывода:

Входной интервал Y - диапазон, содержащий данные результативного признака;

Входной интервал Х - диапазон, содержащий данные факторов независимого признака;

Метки – флажок, который указывает содержит ли первая строка названия столбцов или нет;

Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист – можно задать произвольное имя нового листа.

Щелкните по кнопке ОК.

Поиск по сайту: