 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема: Система одновременных уравнений
Содержание занятия.
1. Определение параметров структурной модели на основе приведенной формы модели
2. Проверка структурной модели на идентификацию.
Литература: [1] стр185-193, [3] стр332-337, [2] стр108-110
Задание №1
На основе приведенной формы модели вида:

построить структурную форму модели.
Методические указания по выполнению задания:
Переходим от приведенной формы к структурной форме модели, т.е. к системе уравнений: 
Для этой цели из первого уравнения приведенной формы модели надо исключить х2 выразив его из второго уравнения приведенной формы и подставив в первое:  . Тогда
. Тогда  . После соответствующих преобразований получим:
. После соответствующих преобразований получим:  - первое уравнение структурной модели.
- первое уравнение структурной модели.
Чтобы найти второе уравнение структурной модели обратимся вновь к приведенной форме модели. Из второго уравнения приведенной формы модели следует исключить х1, выразив его через первое уравнение и подставив во второе:  и
и  .
.  - второе уравнение структурной модели. Структурная форма модели имеет следующий вид:
- второе уравнение структурной модели. Структурная форма модели имеет следующий вид: 
Задание №2
Применив необходимое условие идентификации, определите, идентифицировано ли каждое из уравнений модели.
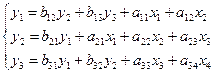
Методические указания по выполнению задания:
Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных отсутствующих в данном уравнении системы, но присутствующих в системе, было бы равно числу эндогенных переменных в данном уравнении без одного. Если обозначить число эндогенных переменных в j-м уравнении системы через H, а число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение – через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила: D+1=H - уравнение идентифицируемо; D+1<H - уравнение неидентифицируемо; D+1>H - уравнение сверхдентифицируемо.
1 уравнение: в нем присутствует три эндогенные переменные  , т.е. Н=3 и две экзогенные переменные – х1, х2, число отсутствующих экзогенных переменных равно двум – х3, х4, т.е. D=2. Имеем равенство: D+1=H (2+1=3).Уравнение идентифицируемо
, т.е. Н=3 и две экзогенные переменные – х1, х2, число отсутствующих экзогенных переменных равно двум – х3, х4, т.е. D=2. Имеем равенство: D+1=H (2+1=3).Уравнение идентифицируемо
Во втором уравнении системы H=2 (y1, y2) и D=1(x4), т.е. D+1+H (1+1=2) Уравнение идентифицируемо
В третьем уравнении системы H=3 (y1, y2,y3), а D=2 (x1,x2), т. е. D+1=H (2+1+3) и это уравнение идентифицируемо. Таким образом, система в целом идентифицируема.
Задание №3
Проверить каждое уравнение системы на необходимое и достаточное условия идентификации:

Методические указания по выполнению задания:
Для первого уравнения Н=3 ( ) и D=2 (х3, х4) , т.е. D+1=H (2+1=3). Необходимое условие идентификации выдержано. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.
) и D=2 (х3, х4) , т.е. D+1=H (2+1=3). Необходимое условие идентификации выдержано. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.
Для проверки на достаточное условие идентификации заполним следующую таблицу коэффициентов при отсутствующих в первом уравнении переменных, в которой определитель матрицы коэффициентов равен нулю.
| Уравнения | Переменные | |
| х3 | х4 | |
| а23 0 | а24 0 |
Det A= a23*0-a24*0=0. Следовательно, достаточное условие идентификации не выполняется и первое уравнение нельзя считать идентифицируемым.
Для второго уравнения Н=2 (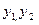 ) и D=1 (х1), т.е. D+1=H (1+1=2). Уравнение идентифицируемо. Достаточное условие идентификации выполняется. Коэффициенты при отсутствующих во втором уравнении переменных составят:
) и D=1 (х1), т.е. D+1=H (1+1=2). Уравнение идентифицируемо. Достаточное условие идентификации выполняется. Коэффициенты при отсутствующих во втором уравнении переменных составят:
| Уравнения | Переменные | |
| у3 | х1 | |
| b13 -1 | а11 а31 |
Det A= b13* а31+а11  0. Ранг матрице равен двум, что соответствует следующему критерию: ранг матрицы коэффициентов должен быть не менее, чем число эндогенных переменных в системе без одного, второе уравнение системы точно идентифицируемо.
0. Ранг матрице равен двум, что соответствует следующему критерию: ранг матрицы коэффициентов должен быть не менее, чем число эндогенных переменных в системе без одного, второе уравнение системы точно идентифицируемо.
Третье уравнение системы содержит Н=3 и D=2, т.е. по необходимому условию идентификации оно точно идентифицируемо D+1=H. Противоположный вывод имеем, проверив его на достаточное условие идентификации. Составим таблицу коэффициентов.
| Уравнения | Переменные | |
| х3 | х4 | |
| 1 2 | 0 а23 | 0 а24 |
Det A= a24*0-a23*0 =0. Достаточное условие идентификации не выполняется. Уравнение неидентифицируемо. Следовательно, рассматриваемая в целом структурная модель, идентифицируемая по счетному правилу, не может считаться идентифицируемой из достаточного условия идентификации.
Поиск по сайту: