Метод простой итерации для нелинейных систем уравнений

Рассмотрим систему двух нелинейных уравненй:

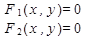
Предположим, что система имеет изолированные корни, которые можно определить графически. Известны начальные приближения корней. Перепишем систему нелинейных уравнений.

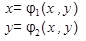
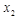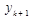Функции и называют интерферирующими, тогда любое последующее приближение и определяется по предыдущему по формулам

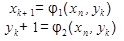
Теорема:

Пусть в некоторой замкнутой окрестности имеется одно и только одно решение системы нелинейных уравнений. .

Если:

1. 1 условие интерферирующая функции определенны и непрерывны дифференцируемы в области R;

2. Начальное и все последующие приближения принадлежат R;

3. В области R выполняется неравенство

или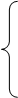

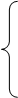
то процесс итераций сходится к решению системы

;

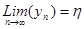
Оценка погрешности k-того приближения определяется неравенством

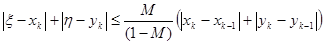
Сходимость метода считается хорошей, если . Если в двух последовательных приближениях совпадает например первые три десятичных знака после запятой, то ошибка последнего округления не превосходит .

Поиск по сайту: