Метод. Метод простой итерации

ВычМат лекция (17.09.12)

Итерационные методы решений линейных уравнений

С вычислительной точки зрения эти методы имеют следующие преимущества:

1. Если итерации сходятся достаточно быстро, то получается выигрыш по времени;

2. В методе итераций требуется гораздо меньшая точность промежуточных вычислений, и погрешность округления сказывается меньше чем в методе Гауса;

3. Методы итераций устойчивы к просчетам в промежуточных вычислениях, по этому их называют само исправляющимися;

4. Итерационные методы особенно выгодны при решении систем в которых значительное число коэффициентов равно 0;

5. Итерационные процессы приводят к выполнению однообразных операций => легко программируются для вычислительной техники.

Метод. Метод простой итерации.

Пусть решается система линейных алгебраических уравнений с неособой матрицей коэффициентов.

Для начала итерационного процесса, система должны быть приведена к каноническому виду. В предположении, что все диагональные коэффициенты матрицы не равны 0.

;

; ; ;

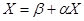Допустим, что известно некоторое нулевое приближение корней.

Ели нет сведений даже о приближенных корнях системы, то за 0 приближение берут столбец свободных членов. Все последующие приближения определяются по формуле:

Если последовательность приближений имеет предел, то он (предел) будет решением системы линейных уравнений.

Сходимость итерационного процесса зависит от свойств матрицы коэффициентов и не зависит от начального приближения.

Конкретно сходимость связанна с нормами матрицы, а любая матрица определяется тремя нормами

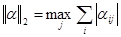
Теоремы:

1. Чтобы последовательность приближений сходилась достаточно чтобы какая-либо из норм матрицы α .

В этой теореме сформулированный достаточные условия сходимости для системы приведенной к каноническому виду. Для исходной системы сходимость так же определяется матрицей коэффициентов A:

Метод итераций сходится если выполняется ; т. е. Модули диагональных коэффициентов должны быть больше суммы модулей остальных коэффициентов в каждой строке матрицы A.

Для многих приложений важно знать какова скорость сходимости приближенного вектора к точному значению. т. е. каким должен быть k, для достижения заданной точности ω.

2. Если одна из норм матрицы , то справедливо следующая оценка погрешности

Норма α одна из норм матрицы A, k – число итераций необходимых для вычисления точности ω.

Эта формула упрощается, если за принять столбец свободных членов.

Поиск по сайту: