Метод Ньютона для систем нелинейных уравнений

Этот метод есть обобщение метода Ньютона для уточнения корней нелинейных уравнений, причем реализуется n итерационных процессов параллельно.

Метод можно применить если могут быть вычислены все частные производные исходных функций по всем переменным. Для начала итерационного процесса надо иметь начальное приближение корней.

Если каждое из исходных уравнений удается преобразовать так, что оно будет выражено функцией одной переменной, то приближенное решение можно найти графически как точку пересечения графика функций. Однако точность графического определения корней недостаточна, здесь и применяют метод Ньютона для уточнения корней.

Пусть заданна система двух нелинейных уравнений.

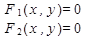
И известно грубое, приближенное решение (). Тогда точное решение можно выразить так

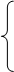
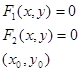
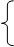Запишем ряд Тейлора функции двух переменных в окрестностях точки

Ограничившись линейными членами относительных невязок ∆x и ∆y получим

Введем обозначения 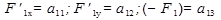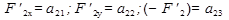в точке .

Тогда получим систему линейных уравнений относительно невязок ∆x, ∆y

Решение этой линейной системы позволит найти невязки. Вычислить новые значения корней, затем принять их за следующее начальное приближение и снова решить систему линейных уравнений.

Если начальное приближение выбрано удачно, процесс итераций сходится быстро с квадратичной точностью.

Условие окончания итерации.

Аналогично выполняем уточнение начальных приближений для системы n нелинейных уравнений, сводя ее к системе n линейных уравнений относительно невязок .

При разработке программы, во избежание зацикливания при неудачном выборе начального приближения корней, следует ограничить количество итераций некоторым числом (20..30 итераций). Если за столько итераций корни не уточняются, то надо вернуться к начальным приближениям и проверить их.

Поиск по сайту: