 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Распределение заданий
Варианты заданий распределяются в зависимости от букв Фамилии Имени и Отчества студента следующим образом:
· Записываются инициалы Фамилии, Имени и Отчества студента, выполняющего задания, а также две последние цифры его персонального кода из студенческого билета или зачетной книжки.
· Слева направо под инициалами подписываются цифры от 1 до 5 по порядку – это порядковые номера заданий.
· Под номерами тем подписываются номера заданий, которые определяются по буквам инициалов из данной ниже таблицы:
| Буквы | А,Я,1 | Б,Р | В,С,2 | Г,Т,Ы,3 | Д,У,4 | Е,Ё,Ф,5 | Ж,Х,6 | З,Н,Ц | И,Ч | Й,Ш,7 | К,Щ,Ъ,8 |
| Номера заданий |
| Буквы | Л,Э,Ь,9 | М,Ю | П | О |
| Номера заданий |
Например:
1. Говоров_Пётр_Иванович_№13825 будет выполнять следующие задания в указанных темах:
| ФИО | Г | П | И | ||
| № темы | |||||
| № варианта |






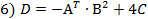









 Для вариантов 1-6 доказать эквивалентности на таблицах истинности:
Для вариантов 1-6 доказать эквивалентности на таблицах истинности:






Для вариантов 7-11 доказать или опровергнуть тождественную истинность (тавтологию) на таблицах истинности:

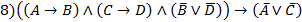


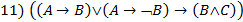
Для вариантов 12-15 выяснить при каких значениях Х, У, Z ложны следующие формулы на таблицах истинности:




 Вычисление вероятностей случайных событий по классической формуле. Теоремы сложения и умножения вероятностей.
Вычисление вероятностей случайных событий по классической формуле. Теоремы сложения и умножения вероятностей.
1) В барабане револьвера 7 гнезд, из них в 5 вложены патроны. Барабан приводится во вращение, потом нажимается спусковой курок. Какова вероятность того, что, повторив такой опыт 2 раза подряд:
а) оба раза не выстрелит;
б) оба раза револьвер выстрелит?
2) Для сигнализации на складе установлены три независимо работающих устройства. Вероятность того, что при необходимости первое устройство сработает, составляет  , для второго и третьего устройства эти вероятности равны соответственно
, для второго и третьего устройства эти вероятности равны соответственно 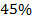 и
и  . Найти вероятность того, что в случае необходимости сработают:
. Найти вероятность того, что в случае необходимости сработают:
а) ни одно устройство;
б) только одно устройство;
в) не менее двух устройств.
3) В группе из 18 студентов имеется 5 отличников. Выбираются наудачу три студента. Какова вероятность, что:
а) все окажутся отличниками;
б) не более двух окажутся отличниками?
4) Студент знает 24 из 30 вопросов по первому разделу и 32 из 35 вопросов по второму разделу курса. На экзамене ему случайным образом предлагается по одному вопросу из каждого раздела курса. Какова вероятность того, что студент ответит правильно:
а) хотя бы на один вопрос;
б) на оба вопроса?
5) Алиса Туманная нашла в коробке своих родителей пять одинаковых кассет с фотопленками, из которых три пленки отсняты, а две – чистые. Будучи не в состоянии установить, какие из них отсняты, Алиса решает отобрать наугад две пленки, а остальные проявить. Какова вероятность того, что в отобранных кассетах окажутся чистыми:
а) обе пленки;
б) хотя бы одна пленка?
6) Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,15. Проверено три изделия. Какова вероятность того, что из них окажутся бракованными:
а) два изделия;
б) не более двух изделий?
7) В магазин поступило 14 ноутбуков, из которых 5 требуют дополнительной установки программного обеспечения. Какова вероятность того, что среди двух отобранных случайным образом для продажи ноутбуков потребуют установки программ:
а) хотя бы один ноутбук;
б) оба ноутбука?
8) Известно, что среди 10 бутылок минеральной воды, этикетки на которых отсутствуют, имеется 4 бутылки производства «Ариант». Какова вероятность того, что среди взятых наугад двух бутылок будет содержаться от производителя «Ариант»:
а) только одна бутылка;
б) хотя бы одна бутылка?
9) Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что эта деталь находится:
а) не более, чем в трех ящиках;
б) не менее, чем в двух ящиках.
10) Монета брошена 4 раза. Найти вероятность того, что:
а) герб выпадет ровно два раза;
б) герб выпадет хотя бы раз.
11) Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что:
а) он промахнется 3 раза;
б) хотя бы один раз попадет.
12) Консультационная фирма получила приглашение для выполнения 2 работ от 2 международных корпораций. Руководство фирмы оценивает вероятность получения заказа от фирмы А (событие А) равной 0,45. Так же по мнению руководителей фирмы, в случае, если фирма заключит договор с компанией А, то с вероятностью 90% компания В даст фирме консультационную работу. С какой вероятностью компания получит:
а) оба заказа;
б) ни одного заказа?
13) Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что:
а) промахнется все 3 раза;
б) попадет 2 раза.
14) Из колоды карт (их 36) вытаскивают наудачу 5 карт. Какова вероятность того, что будут вытащены:
а) 2 туза и 3 шестерки;
б) семерка треф.
15) Для трех розничных торговых предприятий определен плановый уровень прибыли. Вероятность того, что первое предприятие выполнит план равна 90%, для второго она составляет 95%, для третьего 100%. Какова вероятность того, что плановый уровень будет достигнут:
а) только двумя предприятиями;
б) хотя бы один предприятием.
 Решить задачи, применяя формулу полной вероятности или формулу Байеса:
Решить задачи, применяя формулу полной вероятности или формулу Байеса:
1) В специализированную больницу поступают в среднем 50% больных с заболеванием ОРВИ, 30% – с заболеванием Грипп, 20% – с заболеванием пневмония. Вероятность полного излечения болезни ОРВИ равна 0,7; для гриппа и пневмонии эти вероятности равны 0,8 и 0,9 соответственно. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что больной страдал заболеванием ОРВИ.
2) Три сестры: Даша, Маша и Наташа – моют посуду после ужина. Старшая, Маша, моет посуду в половине всех случаев, Даша и Наташа – в четверти каждая. Если посуду моет старшая, то вероятность того, что посуда будет разбита – 0,02. Если это делает Даша, то вероятность – 0,03. Для младшей эта вероятность равна 0,04. Раздался звон разбитой посуды. Найти вероятность того, что на кухне хозяйничала Наташа.
3) Предположим, что 85% людей, которые интересуются возможными инвестициями (вложениями) в брокерскую фирму, не покупают акции, а 33% не покупают облигации. Так же известно, что 28% интересующихся прерывают покупку ценных бумаг – как акции, так и облигации. Некто интересуется делами компании; чему равна вероятность, что он будет покупать либо облигации, либо акции, либо и то и другое?
4) Число грузовых автомашин, проезжающих по шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
5) Среди студентов института по результатам зимней сессии 30% первокурсников имеют только отличные оценки, среди второкурсников таких студентов 35%, на 3 и 4 курсе их 20% и 15% соответственно. По данным деканатов известно, что на первом курсе 20% студентов сдали сессию только на отличные оценки, на втором – 30%, на третьем 35%, на четвертом 40% отличников. Наудачу вызванный студент оказался отличником. Чему равна вероятность того, что он (она) – третьекурсник?
6) Противотанковая батарея состоит из 10 орудий. Для любого из 6 орудий первой нруппы вероятность попадания в цель при одном выстреле равна 0,7. Для любого из 4 орудий второй группы эта вероятность равна 0,9. Наудачу выбранное орудие произвело два выстрела по цели, в результате чего были зафиксированы два попадания. Найти вероятность того, что стрелявшее орудие принадлежит:
а) первой группе;
б) второй группе.
7) В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
8) Укупорка банок томатного сока производится двумя автоматами, продукция которых поступает на общий конвейер. Производительность второго автомата в 1,5 раза выше производительности первого. Доля банок с дефектами упаковки в среднем составляет 0,5% у первого и 0,2% у второго автомата. Какова вероятность того, что взятая наугад банка сока не будет иметь дефекты упаковки?
9) Агент по недвижимости пытается продать участок земли под застройку. Он полагает, что участок будет продан в течение ближайших 6 месяцев с вероятностью 0,9 (если экономическая ситуация в регионе не будет ухудшаться). Если же экономическая ситуация будет ухудшаться, то вероятность продать участок уменьшится до 0,5. Экономист, консультирующий агента полагает, что с вероятностью, равной 0,7 экономическая ситуация в регионе в течение следующих 6 месяцев будет ухудшаться. Чему равна вероятность того, что участок будет продан в течение ближайших 6 месяцев?
10) Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8; для второго – 0,4. После стрельбы в мишень обнаружена одна пробоина. Что более вероятно, попал первый стрелок или нет?
11) В магазин от двух поставщиков поступила женская обувь в одинаковых упаковках. От первого поставщика поступило 480 пар, из них 360 пар обуви черного цвета. От второго поставщика поступило 320 пар, в том числе 120 пар обуви черного цвета. В выбранной наугад упаковке оказалась обувь черного цвета. Какова вероятность того, что она поступила от второго поставщика?
12) Два товароведа производят приемку партии товара по качеству. Вероятность того, что очередное изделие попадет к первому товароведу, составляет 0,55; а ко второму – 0,45. Вероятность пропуска дефекта первым товароведом равна 0,05, а вторым – 0,15. Определить вероятность того, что в процессе приемки дефектное изделие будет обнаружено.
13) Пассажир может обратиться за получением билета в одну из трех касс. Вероятности попадания в каждую кассу зависят от их местонахождения и равны соответственно 0,2; 0,5; 0,3. Вероятности того, что в кассах все билеты проданы, равны соответственно 0,6; 0,9; 0,7. Какова вероятность того, что пассажир приобретет билет? Если пассажир приобрел билет, то в какой из трех касс он вероятнее всего купил билет?
14) Известно, что 5% всех мужчин и 0,25% женщин – дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина? (считать, что мужчин и женщин одинаковое количество).
15) При слиянии акционерного капитала 2 фирм аналитики фирмы, получающей контрольный пакет акций, полагают, что сделка принесет успех с вероятностью, равной 0,65, если председатель совета директоров поглощаемой фирмы выйдет в отставку; если он откажется, то вероятность успеха равна 0,3. Предполагается, что вероятность ухода в отставку председателя составляет 0,7. Чему равна вероятность успеха сделки?

а) Составьте закон распределения дискретной случайной величины Х;
б) вычислите ее математическое ожидание;
в) дисперсию;
г) среднее квадратическое отклонение;
д) начертите ее многоугольник распределения;
Поиск по сайту: