Найти произведения квадратных матриц

Даны матрицы А = , В = , С = 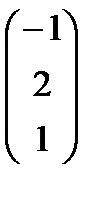и число a = 2. Найти А^ТВ+aС.

A^T = ; A^TB = × = = ;

aC = ; тогда искомая матрица А^ТВ+aС = + = .

При каких значениях переменных X, Y, Z, U ложна следующая формула:

X

Y

Z

U

*

Три стрелка делают по одному выстрелу в цель. Вероятность попадания для первого стрелка 0,8, для второго – 0,7, для третьего – 0,6. Найти вероятность того, что:

а) все стрелки попадут в цель;

б) только один стрелок попадет в цель;

в) только два стрелка попадут в цель;

г) все стрелки промахнутся;

д) цель будет поражена.

Решение:

Обозначим: событие А – первый стрелок попадет в цель

B – второй стрелок попадет в цель

С – третий стрелок попадет в цель

События A, B, C – независимые.

1)

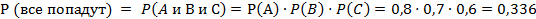
2)

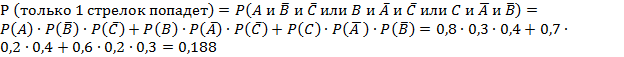
3)

4)

5)

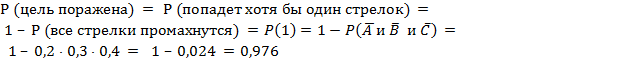
Два консервных завода поставляют в магазин мясные и овощные консервы, причем первый завод поставляет продукции в три раза больше второго. Доля овощных консервов в продукции первого завода составляет 60%, а второго 70%. Для контроля в магазине взято наугад одно изделие.

а) Какова вероятность того, что это окажутся мясные консервы?

б) Взятое изделие оказалось мясными консервами. Какова вероятность, что оно изготовлено вторым заводом?

Решение. Обозначим: событие А – взяты мясные консервы;

событие Н₁ – изделие изготовлено I заводом;

событие Н₂ – изделие изготовлено II заводом.

По условию задачи первый завод поставляет продукции в три раза больше, чем второй, то есть Р (Н₁) > Р (Н₂) в три раза, или Р (Н₁) = 3 × Р (Н₂).

Вероятность того, что консервы мясные, для первого завода составляет 40%, то есть
, для второго завода 30%, то есть .

а) Учитывая, что событие А произойдет обязательно с одним из событий (гипотез) Н_i, образующих полную группу, применим формулу полной вероятности:

б) По условию событие А произошло, то есть взяты мясные консервы. Тогда вероятность гипотезы Н₂ – консервы изготовлены вторым заводом – находим по формуле Байеса

Котировки акций могут быть размещены в Интернете на трех сайтах. Материал есть на первом сайте с вероятностью 0,7, на втором – с вероятностью 0,6, на третьем – 0,8. Студент переходит к новому сайту только в том случае, если не найдет данных на предыдущем. Составить закон распределения числа сайтов, которые посетит студент.

Найти:

1) функцию распределения этой случайной величины и построить ее график;

2) математическое ожидание и дисперсию этой случайной величины.

Решение:

Вероятность того, что студент нашел всю информацию с 1 сайта:

0,7*0,4*0,2+0,3*0,6*0,2+0,3*0,4*0,8=0,188

Вероятность того, что студент нашел всю информацию с 2х сайтов:

0,7*0,6*0,2+0,7*0,4*0,8+0,3*0,6*0,8=0,452

Вероятность того, что студент нашел всю информацию с 3х сайтов:

0,7*0,8*0,6=0,336

Вероятность того, что студент не нашел информацию ни с одного из сайтов:

1-0,336-0,452-0,188=0,024

1) F(x<0)=0 1 F(x)

F(0<=x<1)=0.024

F(1<=x<2)=0.212

F(2<=x<3)=0.664

F(3<=x)=1

0 1 2 3 x

2) M(x)=0*0.024+1*0.188+2*0.452+3*0.336=0.188+0.904+1.008=2.1

D(x)=M(x²)–M²(x)=0*0.024+1*0.188+4*0.452+9*0.336-4.41=0.61

Вопросы для самоподготовке к контрольным тестам по темам

1. Определение матрицы и действия над матрицами.
2. Понятие «высказывание». Предикаты.
3. Отрицание. Конъюнкция. Импликация. Эквивалентность. Дизъюнкция. Определение. Таблица истинности.
4. Тавтология.
5. Приоритетность выполнения логических операций.
6. Что включает в себя понятие «теория вероятностей»?
7. Что является задачей теории вероятностей?
8. Что включает в себя понятие «испытание»?
9. Что называется событием?
10. Как обозначаются события?
11. Какое событие называется достоверным? невозможным? случайным?
12. Дайте определение событий совместимых (совместных) и несовместимых (несовместных).
13. Какие события называются противоположными? Как обозначаются противоположные события?
14. Что называется произведением событий?
15. Поясните следующее понятие «полная группа событий».
16. Дайте понятие «благоприятствующее событие».
17. Что называется вероятностью события?
18. Классическое определение вероятности.
19. Какие значения может принимать вероятность события?
20. Статистическое определение вероятности.
21. Теорема сложения вероятностей несовместимых событий.
22. Теорема сложения вероятностей совместимых событий.
23. Понятие зависимых и независимых событий.
24. Понятие условной вероятности.
25. Теорема умножения вероятностей (вероятность произведения двух зависимых событий).
26. Теорема умножения вероятностей (вероятность произведения двух независимых событий).
27. Формула полной вероятности.
28. Формула Байеса.
29. Формула Бернулли.
30. Случайная дискретная величина и ее закон распределения.
31. Математическое ожидание дискретной случайной величины и его основные свойства.
32. Дисперсия и ее свойства.

Поиск по сайту: